Das Damenproblem ist ein Klassiker aus dem 19.Jahrhundert, der Blütezeit der Schachknobeleien. Es geht darum, acht Damen auf einem 8⨉8 Schachbrett so anzuordnen, dass keine Dame eine andere schlagen kann. Mit der Frage, wie viele Möglichkeiten es dafür gibt, wird aus dem Schachproblem ein Problem aus der Kombinatorik. Der bayrische Schachmeister Max Bezzel formulierte die Schachfrage 1848 und man weiß, dass Carl Friedrich Gauss, der von der mathematischen Variante in der Leipziger Illustrierten Zeitung las (wo das Problem veröffentlicht worden war), auch ausgiebig daran herumknobelte.
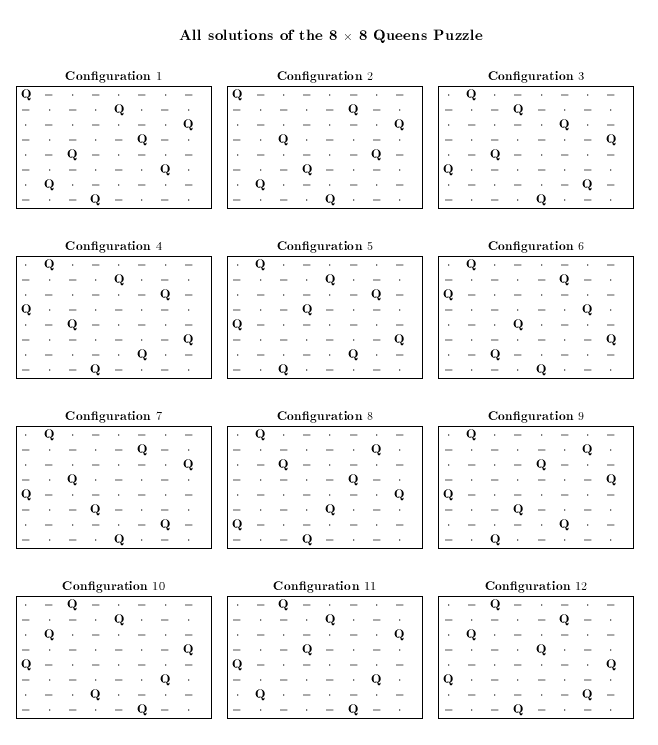
Die richtige Zahl (92) fand aber ausnahmsweise mal nicht Gauss, sondern ein Gymnasiallehrer namens Franz Nauck aus Schleusingen. Für das verallgemeinerte Damenproblem, also n⨉n Felder kennt man inzwischen die Anzahl der Lösungen Q(n) bis zu n=26 (nämlich: Q(26)=22.317.699.616.364.044). Es wird vermutet, dass das Verhältnis des Logarithmus von Q(n) zu n log(n) konvergiert.
Nun haben die drei Amerikaner Seth Chaiken (University at Albany), Christopher R. H. Hanusa (Pittsburgh) und Thomas Zaslavsky (MIT) sich das Problem nochmals vorgenommen, und wie es sich für Mathematiker gehört: gehörig verallgemeinert.
Chaiken, Hanusa und Zaslavsky untersuchten, wie viele Möglichkeiten es gibt, q Spielsteine auf ganzzahligen Gitterpunkten im Inneren eines konvexen Polygons mit rationalen Eckpunkten zu platzieren, ohne dass sich die Steine gegenseitig bedrohen, wobei die Spielsteine irgendwelchen Zugregeln unterliegen. Das Spielbrett muss also nicht aussehen wie ein Schachbrett, sondern kann auch zum Beispiel wie ein unregelmäßiges Sechseck aussehen, und es muss auch nicht um Damen gehen: Möglich wären zum Beispiel auch Läufer oder fiktive Steine wie Nachtreiter (das sind Springer, die beliebig oft weiterspringen können, so lange die angesprungenen Felder alle auf einer Geraden liegen).
Um die Anzahl der Konfigurationen zu bestimmen, verwenden Chaiken, Hanusa und Zaslavsky ein Hilfsmittel, das in der Kombinatorik derzeit extrem populär ist: Ehrhart-Theorie. Entwickelt wurde sie vom französischen Mathematiker Eugène Ehrhart in den 1960er Jahren, und mit ihnen kann man ganzzahlige Gitterpunkte in Polyedern zu zählen. Chaiken, Hanusa und Zaslavsky stellen die Aufstellungen der Figuren als Punkte in einem hochdimensionalen Polyeder dar und schneiden \"verbotene\" Aufstellungen - in denen sich zum Beispiel zwei Damen bedrohen - höchst trickreich durch Hyperebenen ab. Die verbleibenden Gitterpunkte werden nach der Methode von Ehrhart gezählt, und so erhält man als Ergebnis, dass sie als Quasi-Polynom - eine Art Verallgemeinerung von Polynomen, bei denen die Koeffizienten nicht mehr Konstanten, sondern ihrerseits periodische Funktionen sind - dargestellt werden können: Klar, denn Ehrhart-Polynome sind Quasi-Polynome. Puh.
Und wie viele Aufstellungen gibt es nun? Für einige Spezialfälle werten Chaiken, Hanusa und Zaslavsky die Ehrhart-Polynome aus und vergleichen sie mit Ergebnissen, die der tschechische Amateurmathematiker und Schachfanatiker Vaclav Kotesovec (ohne Beweise) auf seiner Webseite angibt - und diese Ergebnisse scheinen alle zu stimmen.
Und wie lauten nun die konkreten Zahlen? Dafür versprechen die Autoren einen zweiten Teil für ihr Paper. Und der ist erst in Arbeit.
Andreas Loos
