Dem russischen Mathematiker Yaroslav Shitov ist es kürzlich gelungen, in einem lediglich drei Seiten langen Artikel die Vermutung von Hedetniemi (1966) mit einem Gegenbeispiel zu widerlegen: Es gibt Graphen, bei denen die chromatische Zahl des Tensorproduktes kleiner ist als das Minimum der chromatischen Zahlen der Faktorgraphen. Unter Experteninnen und Experten gilt diese Entdeckung als Sensation. Doch was hat es mit der Vermutung von Hedetniemi auf sich? Und was genau sind Tensorprodukte und chromatische Zahlen? Versuch einer Erklärung.
Ein Beispiel für die vielfältige Anwendbarkeit der Mathematik ist die Anwendbarkeit der Graphentheorie, einem Teilgebiet der Mathematik. Die Gründe dafür sind bei genauerer Betrachtung wenig überraschend: Denn da ein Graph (nicht zu verwechseln mit den aus der Schule bekannten Funktionsgraphen!) nichts anderes ist als eine Menge, bei der zwischen je zwei Elementen Verbindungen bestehen können oder nicht, lassen sich mit diesem Konzept eine enorme Anzahl von Problemstellungen „aus dem echten Leben“ mathematisch fassen. Beispiele dafür sind U-Bahnpläne, Moleküle, Stadtpläne, Fahrrouten etc.
Beispiel für einen Graphen. Knoten (grau) und Verbindungen zwischen ihnen; mehr braucht es nicht, um einen Graphen zu definieren.(eigene Abb.)
U-Bahnpläne sind Beispiele für Graphen aus dem Alltag.(eigene Abb.)
Die Vermutung von Hedetniemi nimmt Bezug auf eine wichtige Kenngröße für Graphen: Die chromatische Zahl \(\chi(G)\). Sie gibt an, wie viele Farben man mindestens braucht, um die Knoten eines Graphen so einzufärben, dass zwei verbundene Knoten nicht die gleiche Farbe haben.
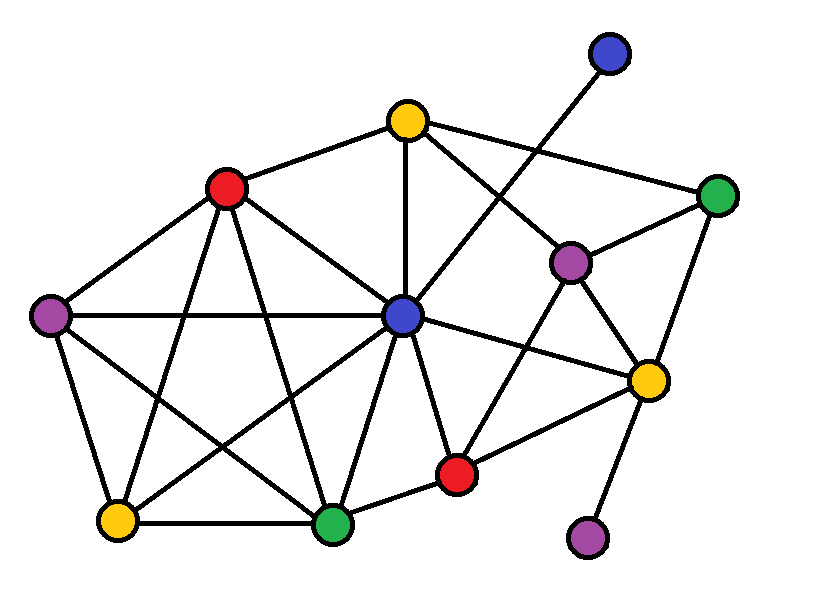Dieser Graph ist mit fünf Farben einfärbbar; das „Pentagramm“ unten links sorgt dafür, dass weniger als fünf Farben nicht ausreichen.
(eigene Abb.)
Ein auch außerhalb der Fachwelt bekanntes Beispiel für eine Aussage über chromatische Zahlen ist der sogenannte Vierfarbensatz. Er besagt, dass planare Graphen, also jene Graphen, die sich in der Ebene zeichnen lassen, ohne, dass Kanten sich überschneiden, eine chromatische Zahl von höchstens vier haben. Die populärwissenschaftliche Version des Vierfarbensatzes besagt, dass man jede Landkarte mit höchstens vier Farben einfärben kann, sodass zwei benachbarte Länder nicht aneinandergrenzen. Der Zusammenhang von planaren Graphen und Landkarten stellt sich wie folgt her: Jeder Landkarte kann man einen planaren Graphen zuordnen, in dem man die Länder als Knoten betrachtet und zwei Knoten mit einer Kante verbunden sind, wenn die entsprechenden Länder aneinander Grenzen; ebenso kann man jedem planaren Graphen eine entsprechende Landkarte zuordnen.
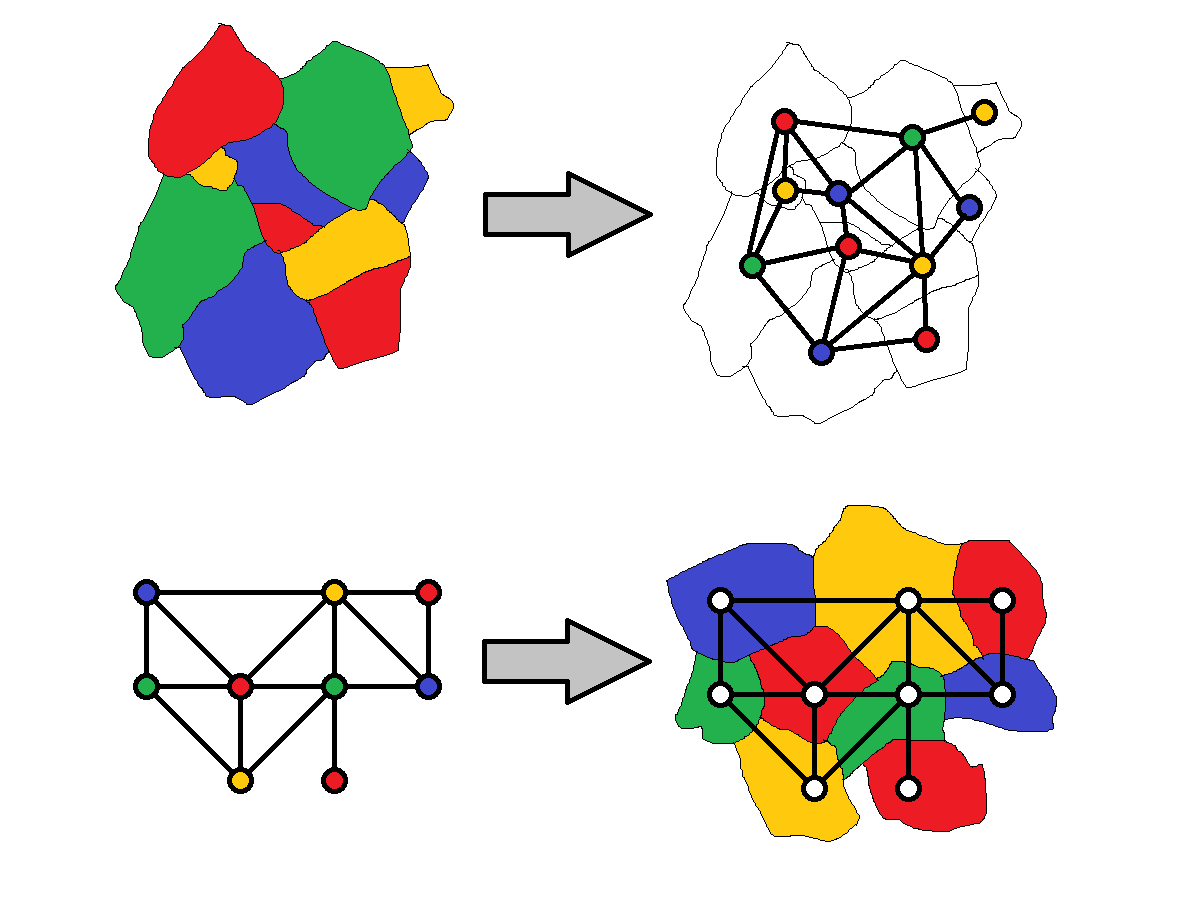Landkarten und planare Graphen sind im Wesentlichen das Gleiche. Der Vierfarbensatz besdagt, dass für eine Färbung vier Farben stets genügen.
(eigene Abb.)
Über die Zeit haben Mathematikerinnen und Mathematiker eine Vielzahl von Möglichkeiten untersucht, gegebene Graphen zu neuen zu verknüpfen; man kann sie beispielsweise zusammenlegen (das ist die sogenannte disjunkte Vereinigung), vollständig verbinden (diese Konstruktion wird Join genannt), oder sogar, in einem gewissen Sinne, miteinander multiplizieren. Über den letztgenannten Typ von Verknüpfung, dem sogenannten Tensorprodukt, macht die Vermutung von Hedetniemi eine Aussage.
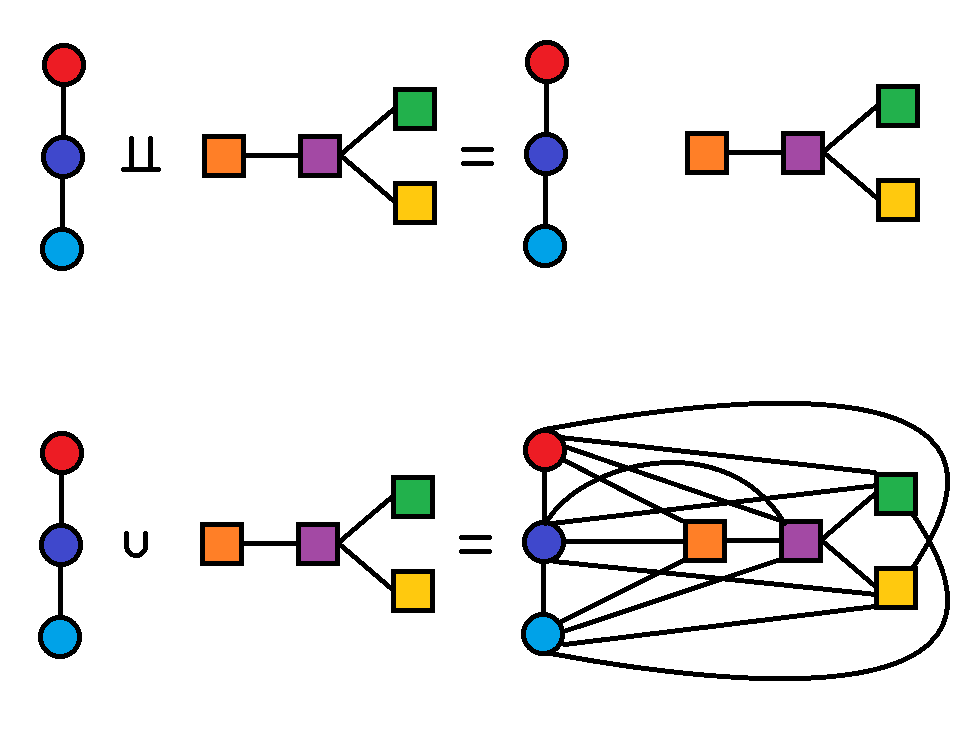Bei der Disjunkten Vereinigung \(G\coprod H\) werden die Graphen einfach zusammengelegt. Beim Join \(G\bigcup H\) wird jeder Knoten des einen mit jedem Knoten des anderen Graphen Verbunden.)
(eigene Abb.)
Das Tensorprodukt zweier Graphen abstrahiert die Multiplikation auf graphentheoretischer Ebene: Die Knoten im Tensorprodukt sind Paare von Knoten der beiden Ausgangsgraphen, und zwei Paare von Knoten werden als verbunden erklärt, wenn sowohl die Knoten des einen Graphen, als auch die Knoten des anderen Graphen verbunden sind.
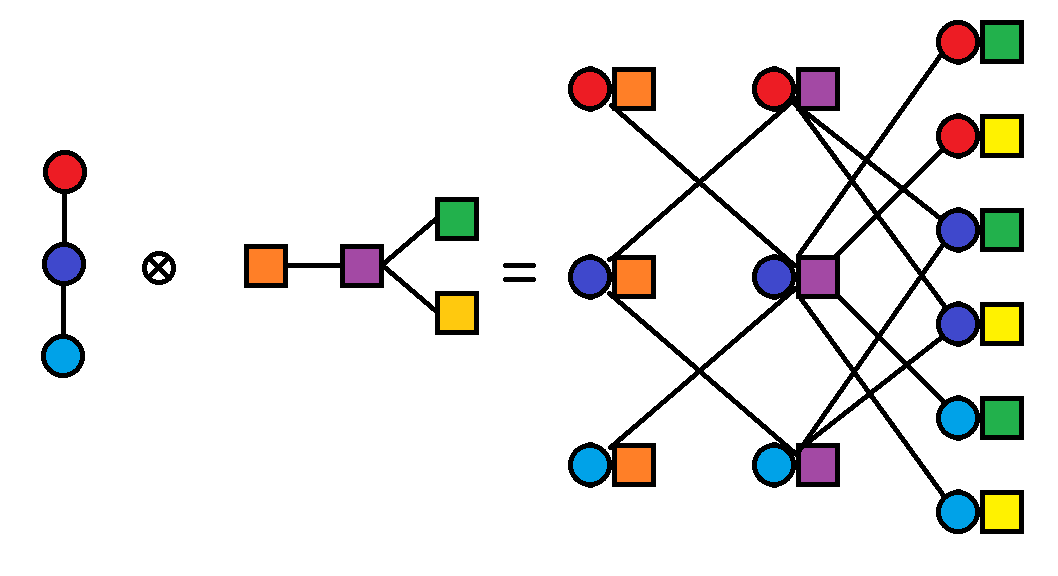Im Tensorprodukt \(G\otimes H\)werden Paare von Knoten nur dann verbunden, wenn die einzelnen Teile bereits vorher verbunden waren: (Blau, Orange) ist bspw. mit (Rot, Violett) verbunden, weil sowohl Blau und Rot, als auch Orange und Violett verbunden sind.
In der Graphentheorie werden derartige Verknüpfungen von Graphen oft in Hinblick auf die chromatische Zahl untersucht: Wenn man die chromatische Zahl beider Bestandteile kennt, was kann man dann über die chromatische Zahl der Verknüpfung aussagen?
Bei der disjunkten Vereinigung ist der Zusammenhang klar: Wenn bei der disjunkten Vereinigung eine Menge von Farben für beide Teilgraphen ausreicht, dann offenbar auch für die disjunkte Vereinigung, es gilt daher: \(\chi(G \coprod H)=\max \{\chi(G), \ \chi(H)\}\).
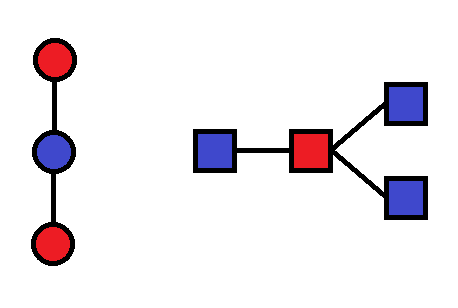Eine Färbung, die für beide Teilgraphen valide ist, ist auch für die disjunkte Vereinigung valide.
(eigene Abb.)
Für den Join lässt sich zeigen, dass die chromatische Zahl genau die Summe der beiden chromatischen Zahlen ist: Dass die Summe der chromatischen Zahlen als Menge von Farben ausreicht, ist klar. Dass es nicht besser geht, sieht man ein, indem man einen der beiden Teilgraphen mit Rottönen und den anderen in Blautönen färbt. Gäbe es nun eine mit weniger Farben auskommende Färbung, müsste zumindest ein Knoten aus dem rötlich gefärbten Graphen mit einem Blauton aus dem anderen Graphen eingefärbt sein (oder andersrum). Da dieser Knoten aber mit jedem anderen bläulich gefärbten Knoten verbunden ist, kann eine solche Färbung nicht mehr valide sein, Widerspruch! Also gilt: \(\chi(G \bigcup H)=\chi(G) + \chi(H)\).
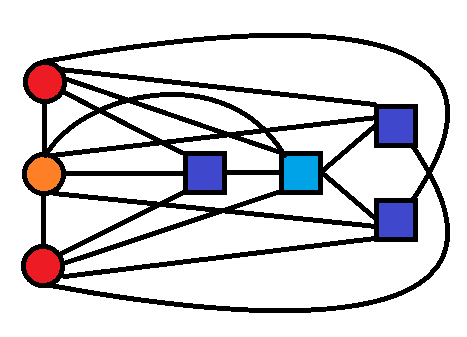Färbt man den einen Graphen in Rottönen und den anderen in Blautönen, sieht man, dass seine chromatische Zahl genau die Summe der Chromatischen Zahlen der einzelnen Bestandteile ist.
(eigene Abb.)
Bei der chromatischen Zahl des Tensorproduktes gestaltet sich die Situation schwieriger. Was klar ist: Wenn eine Färbung für den einen Faktorgraphen valide ist, so auch für das Tensorprodukt. Es gilt also \(\chi(G \otimes H) \leq \min{ \{\chi(G),\ \chi(H)\}}\).
Hat man eine valide Färbung eines Faktorgraphen, kann man sofort eine valide Färbung des Tensorproduktes erhalten.
(eigene Abb.)
Ja, so die Vermutung von Hedetniemi, zumindest für Graphen mit endlich vielen Knoten. Der Graphentheoretiker vermutete im Jahre 1966, dass die chromatische Zahl des Tensorproduktes stets gleich dem Minimum der chromatischen Zahlen der Faktorgraphen ist. Und in der Tat ist es bis vor kurzem niemanden gelungen, ein solches Gegenbeispiel zu konstruieren, was für Laien oft als Indiz für die Richtigkeit einer mathematische Vermutung missgedeutet wird. Doch abseits des Fehlens von Gegenbeispielen hatte die Vermutung von Hedetniemi auch mathematische Indizien: Es ist nicht unvernünftig, anzunehmen, dass in der Konstruktion des Tensorproduktes zweier Graphen die Komponenten der Knoten zu wenig „miteinander zu tun“ haben, als dass sie einen Graphen erzeugen könnten, der die chromatische Zahl der Faktoren unterbietet – Das Verbinden von Knoten durch Kanten wird schließlich komponentenweise auf die Faktorgraphen zurückgeführt.
Für die Konstruktion seines Gegenbeispiels griff Shitov wesentlich auf den Begriff des Exponentialgraphen zurück, einem Graphen, bei dem Graphenfärbungen selber als Knoten betrachtet werden. Mit Hilfe des Exponentialgraphen (und weiterer komplizierter Hilfsmittel wie der rationalen chromatischen Zahl, einer Verallgemeinerung des oben definierten Begriffes der chromatischen Zahl auf rationale Zahlen) gelingt es Shitov in seinem lediglich drei Seiten langen Publikation zwei Graphen zu konstruieren, von denen er zeigen kannonnte, dass die chromatische Zahl ihres Tensorproduktes echt kleiner sein muss als das Minimum der chromatischen Zahlen ihrer Faktoren: Die Vermutung von Hedetniemi ist demnach falsch.
Dass sich eine Vermutung in der Graphentheorie sich als falsch herausstellt, ist übrigens keine Seltenheit: 1946 konnte Tutte eine 1884 von P.T. Tait aufgestellte Vermutung über sogenannte kubische Graphen, das sind Graphen, bei denen jeder Knoten auf drei Kanten trifft, widerlegen. 1979 gelang dem US-Amerikaner Paul Catin ein Gegenbeispiel für die Vermutung von Hajos zu konstruieren, die Aussagen über gewisse Unterstrukturen von Graphen mit chromatischer Zahl \(k\) machen.
Dennoch gelten derartige Gegenbeispiele in der Fachwelt oft als Sensationen – halten sie uns doch vor Augen, dass Dinge, die wahr erscheinen, nicht notwendigerweise wahr sein müssen, und dass, auf dem Pfad der mathematischen Erkenntnis, Erfahrung und Intuition manchmal nicht die idealen Wegweiser sind, die sie zu sein scheinen. Insofern lehren sie uns, wie im echten Leben, aufmerksam zu sein und bei der Suche nach Wahrheit nach Antworten zu suchen und nicht bloß auf Indizien und Anhaltspunkte zu vertrauen.
Konrad Krug