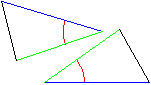
Mathematik zwischen Strenge und Verständlichkeit. Wir besprechen weiter David Ruelle's Buch "Wie Mathematiker ticken": Auch im zweiten Kapitel geht es erstmal nur um Grundlagen, nämlich darum, was Mathematik ist, genauer: was Beweise sind. (Hatten wir hier schon mal diskutiert.) Er beginnt mit einer offensichtlichen geometrischen Tatsache, dem Kongruenzsatz SWS (Dreiecke sind kongruent, wenn zwei Seiten und der eingeschlossene Winkel gleich sind): ellroth den er in aller Ausführlichkeit erläutert.

Tatsächlich werden ihnen diese Überlegungen, sobald Sie verstanden haben, was genau gemeint ist, vermutlich furchtbar trivial und offensichtlich erscheinen. [...] Tatsächlich aber lassen sich aus ziemlich offensichtlichen Behauptungen wie dieser mit unfehlbarer Logik interessante Ergebnisse wie der Satz von Pythagoras ableiten:

Am linken Bild sieht man (durch Berechnen der Flächeninhalte): <br>(a+b)²=c²+4ab/2, woraus sich der Pythagoras direkt ergibt. Der SWS steckt hier implizit im Beweis: man benutzt, daß die gelben Dreiecke alle denselben Flächeninhalt ab/2 haben. (<a href="https://de.wikipedia.org/wiki/Hilberts_Axiomensystem_der_euklidischen_Geometrie">Bei Hilbert</a> ist übrigens SWS  tatsächlich ein Axiom. Klassisch bewies man SWS, indem man zeigte, daß sich ein Dreieck mit Zirkel und Lineal aus den 3 gegebenen Größen konstruieren läßt. Wirklich formal herleiten läßt sich das aus Euklids Axiomen aber nicht, deshalb <a href="https://de.wikipedia.org/wiki/Hilberts_Axiomensystem_der_euklidischen_Geometrie">Hilberts Axiomatisierung</a>.) Es wird dann erklärt, was <strong>Axiome, Theoreme, Definitionen</strong> sind, Gödels Unvollständigkeitssatz kommt kurz vor (später im Buch ausführlicher), es wird klargestellt, daß "Mathematik, wie Mathematiker sie betreiben" nicht nur das Anhäufen von logisch aus den Axiomen abgeleiteten Behauptungen, sondern die Suche nach <em>interessanten</em> Ergebnissen, die sich zu <strong>bedeutungsvollen und natürlichen Strukturen</strong> zusammenfügen, ist, und es wird schließlich diskutiert, daß Mathematiker <strong>im Prinzip auf eine natürliche Sprache verzichten</strong> können: <blockquote>Warum nur im Prinzip und nicht tatsächlich? Weil eine formalisierte Mathematik so unhandlich und undurchsichtig wäre, daß sie in der Praxis vollkommen unbeherrschbar wäre. [...] Mathematische Texte stehen somit in einem ständigen Spannungsfeld: <strong>Die Notwendigkeit der Strenge zwingt zu einem formalisierten Stil, gleichzeitig zwingt die Notwendigkeit, verständlich zu sein, zu einer informellen Erläuterung mit Hilfe der Ausdrucksmittel einer natürlichen Sprache</strong>.</blockquote> Zwei Beispiele für die Spannbreite mathematischer Texte: <blockquote> der <em>Cours d'arithm&eacute;tique</em> von <a href="https://de.wikipedia.org/wiki/Jean-Pierre_Serre">Jean-Pierre Serre</a> und die Rezension "Differentiable dynamical systems" von <a href="https://de.wikipedia.org/wiki/Smale">Steve Smale</a>. In ihrem Stil sind diese beiden Texte sehr unterschiedlich - Serre drückt sich formaler aus, Smale dagegen weniger formal. Smale verwendet handgezeichnete Abbildungen, um seine mathematischen Konstruktionen zu erklären, was Serre vermeiden würde. Trotz der deutlichen stilistischen Unterschiede aber würden wohl die meisten Mathematiker Serres Buch und Smales Artikel als Meisterwerke der schriftlichen Arbeit bezeichnen. Screenshot: Serre: "A course in arithmetic" vs. Smale: "Differentiable dynamical systems" <br> <br> <br><a href="https://www.scienceblogs.de/mathlog/2010/05/ruelle-wie-mathematiker-ticken.php">Ruelle: Wie Mathematiker ticken</a> <a href="https://www.scienceblogs.de/mathlog/2010/05/ruelle-1-wissenschaftliches-denken.php">1 Wissenschaftliches Denken</a> <a href="https://www.scienceblogs.de/mathlog/2010/05/ruelle-2-was-ist-mathematik.php">2 Was ist Mathematik?</a> 3 Das Erlanger Programm 4 Mathematik und Ideologie 5 Die Einheitlichkeit der Mathematik 6 Ein kurzer Blick auf algebraische Geometrie und Arithmetik 7 Mit Alexander Grothendieck nach Nancy 8 Strukturen 9 Die Rechenmaschine und das Gehirn 10 Mathematische Texte 11 Ehrungen 12 Die Unendlichkeit: Nebelwand der Götter 13 Fundamente 14 Strukturen und die Entwicklung von Konzepten 15 Turings Apfel 16 Mathematische Erfindung: Psychologie und Ästhetik 17 Das Kreistheorem und ein unendlich-dimensionales Labyrinth 18 Fehler! 19 Das Lächeln der Mona Lisa 20 „Tinkering" und die Konstruktion mathematischer Theorien 21 Mathematische Erfindung 22 Mathematische Physik und emergentes Verhalten 23 Die Schönheit der Mathematik