Seid umschlungen, Millionen (Schiller) Die Bilder von Jos Leys zeigen eine Kleeblatt-Schlinge (in dunkelgrün) und dann in hellgrün verschiedene Knoten, die die Kleeblatt-Schlinge umschlingen, ganz rechts zwar nicht Millionenfach aber wohl doch einige Hundert mal. In den letzten Wochen hatten wir über Knoten im Lorenz-Attaraktor geschrieben und daß diese Knoten modular sind. Eine Anwendung (dazu nächste Woche) ist die Berechnung der Verschlingungszahl von Knoten im Lorenz-Attraktor. Heute zunächst zur Definition der Verschlingungszahl. Die Verschlingungszahl soll messen, wie verschlungen zwei Knoten miteinander sind. Anschaulich ist es sicher klar, daß im Bild oben die Knoten von links nach rechts eine immer größere Verschlingungszahl mit der Kleeblatt-Schlinge haben.

Verschlingungszahl

Wie definiert man die Verschlingungszahl (engl.: linking number) zweier Knoten? Am einfachsten ist die Verschlingungszahl mit einem unverknoteten Kreis: man denkt sich den unverknoteten Kreis als Rand einer Kreisscheibe und zählt, wie oft der zweite Knoten diese Kreisscheibe schneidet:

linking number 1

linking number 2

linking number 3

Allerdings muß man aufpassen, in welche Richtung der zweite Knoten die Fläche schneidet, ob von oben nach unten oder von unten nach oben. Im folgenden Bild schneidet der zweite (blaue) Knoten die Fläche von oben nach unten und dies zählt als linking number -1: (Warum muß man diese Schnitte negativ zählen? Man kann den zweiten Knoten verformen, ohne seinen topologischen Typ zu ändern, so daß z.B. zwei neue Schnitte mit der Fläche dazukommen, ein positiver und ein negativer. Die Anzahl der ohne Vorzeichen gezählten Schnittpunkte würde also nicht vom topologischen Typ der Knoten abhängen, siehe das Tafelbild weiter unten.) Langer Rede kurzer Sinn: der unverknotete Knoten ist Rand einer Fläche, die zwei Seiten ('oben' und 'unten') hat. Die Verschlingungszahl mit einem zweiten Knoten ist definiert als + plus die Anzahl von dessen Schnittpunkten von 'unten' nach 'oben' - minus die Anzahl von dessen Schnitpunkten von 'oben' nach 'unten' mit dieser Fläche.

Seifert-Flächen

Um das zu verallgemeinern auf verknotete Knoten, benutzt man das man in jeden Knoten eine Fläche einspannen kann, die sogenannte Seifert-Fläche. Daß es eine solche Fläche gibt, suggerieren die folgenden Bilder von Knoten mit eingespannten Flächen Das allgemeine Konstruktionsprinzip ist sehr einfach: Man nimmt eine Projektion des Knotens auf die Ebene, färbt die eingeschlossenen Flächen (in der Ebene) abwechselnd schwarz und weiß: Konstruktion von Seifert-Flächen

dann nimmt man (z.B.) die schwarzen Flächen und klebt sie an den Überkreuzungen mit einem getwisteten Band zusammen. (Die getwisteten Bänder kann man im Bild rechts besonders gut erkennen.) Man muß ein bißchen vorsichtig sein, weil dieses Konstruktionsverfahren evtl. eine einseitige Fläche liefern kann, z.B. ein Möbiusband, und dann läßt sich positive/negative Richtung nicht definieren. Tatsächlich kann man aber das Konstruktionsverfahren noch ein wenig verbessern und immer eine zweiseitige Fläche bekommen, womit sich die Verschlingungszahl dann definieren läßt.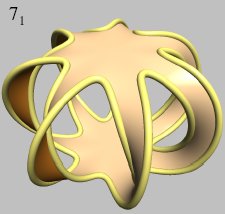

Die Seifert-Fläche eines Knotens ist natürlich nicht eindeutig bestimmt: man kann z.B. an eine Seifert-Fläche noch einige Henkel anhängen (die den Knoten nicht berühren) und bekommt eine andere Seifert-Fläche desselben Knotens.

Wohldefiniertheit

Nachdem man in einen Knoten eine Seifert-Fläche eingespannt, kann man seine Verschlingungszahl mit einem zweiten Knoten definieren: die Verschlingungszahl ist die Anzahl der (je nach Richtung positiv resp. negativ gezählten) Schnittpunkte der Seifert-Fläche mit dem zweiten Knoten. Diese Definition hängt zunächst von einigen 'Wahlen' ab: wir haben eine Seifert-Fläche gewählt (es gibt aber auch andere) und wir haben den zweiten Knoten fest gewählt (man könnte ihn auch verschieben oder irgendwie verformen). Tatsächlich hängt der Wert der Verschlingungszahl aber nicht von diesen beiden 'Wahlen' ab, die Verschlingungszahl ist also "wohldefiniert". Das sieht man am folgenden Bild. Eine Verformung des zweiten Knotens führt entweder zu keinen neuen Schnittpunkten oder (wie im Bild rechts) zu Paaren neuer Schnittpunkte, von denen der eine positiv, der andere negativ gezählt wird. (In der Summe heben sie sich also auf.) Das Anhängen von Henkeln (Bild mitte) and die Fläche ändert die Verschlingungszahl ebenfalls nicht - man kann den zweiten Knoten ja so verschieben, daß er die neuen Henkel gar nicht trifft:

Physikalische Anwendungen

In TvF 22 hatten wir schon mal über den Stromfluß in verschlungenen Drähten geschrieben: man hat zwei Drähte und lasse einen Strom der Stromstärke I durch den ersten Draht fließen, dieser Strom induziert ein Magnetfeld, und damit auch einen Stromfluß im zweiten Draht, mit Stromstärke J. Das Verhältnis J / I der beiden Stromstärken ist dann gerade die Verschlingungszahl der beiden Drähte. Falls man die Verschlingungszahl nicht topologisch definieren will, sondern lieber eine Formel hat, kann man sie mit dem Biot-Savart-Gesetz und dem Ampere-Gesetz berechnen (Gauß 1833):