Calabi-Yau-Mannigfaltigkeiten beschreiben die 6 zusätzlichen Dimensionen in der Stringtheorie. Ein am Mittwoch auf dem ArXiv erschienener Preprint konstruiert nun die 'kleinst-möglichen' Calabi-Yau-Mannigfaltigkeiten. Bekanntlich geht man in der (supersymmetrischen) Stringtheorie von 10 Dimensionen aus: die 4-dimensionale Raum-Zeit und eine 6-dimensionale kompakte Calabi-Yau-Mannigfaltigkeit (das ist eine Kähler-Mannigfaltigkeit mit c₁=0). Es gibt viele Beispiele von Calabi-Yau-Mannigfaltigkeiten, zum Beispiel die Lösungsmenge der Gleichung (in komplexen homogenen Koordinaten, d.h. 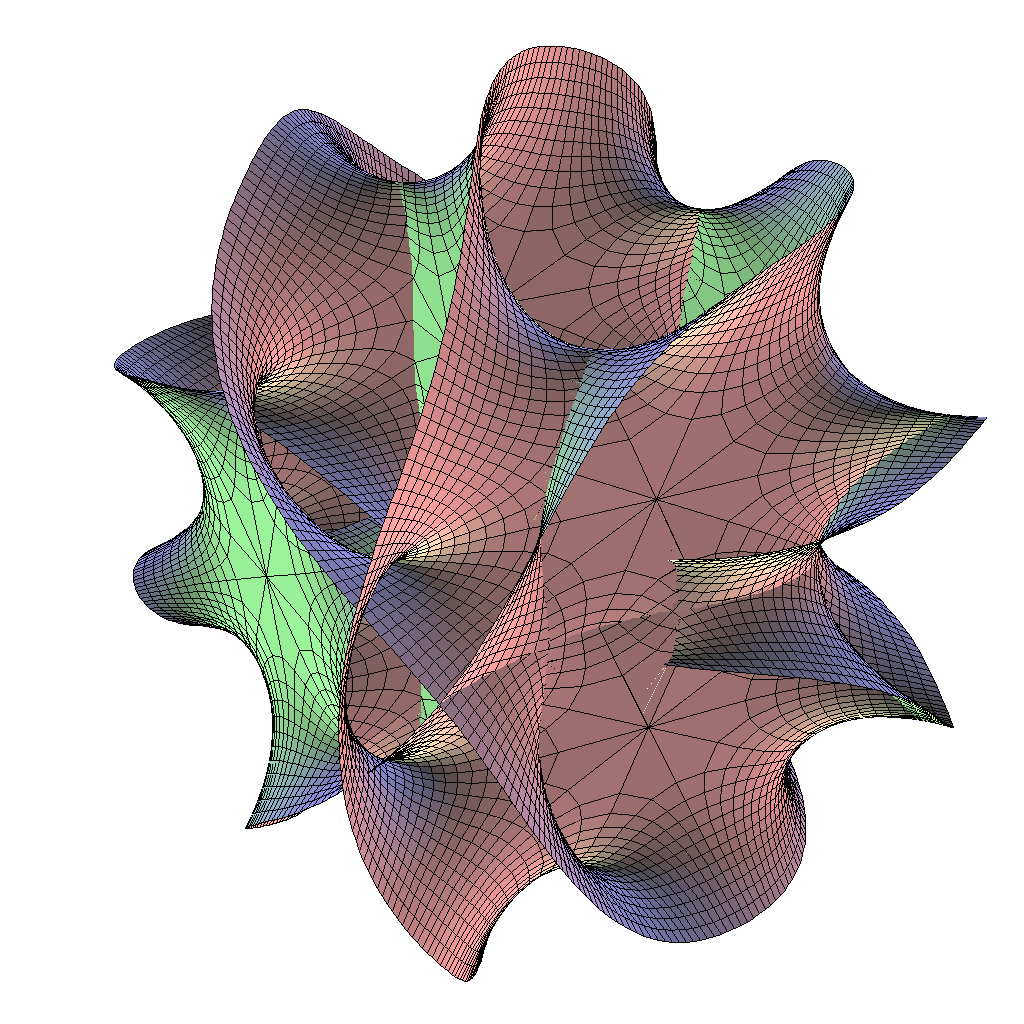im P⁴(C)) z₁⁵+z₂⁵+z₃⁵+z₄⁵+z₅⁵=0: Eine wichtige Invariante von Calabi-Yau-Mannigfaltigkeiten sind ihre Hodge-Zahlen h^p,q. (Nach deRham-Theorie kann man ja die Kohomologie einer differenzierbaren Mannigfaltigkeit mittels Differentialformen berechnen, nach dem Satz von Hodge werden Kohomologieklassen durch eindeutige harmonische Formen repräsentiert, wobei Klassen in der k-ten Kohomologie durch harmonische k-Formen repräsentiert werden. Für Kähler-Mannigfaltigkeiten hat man noch eine zusätzliche Gradierung für harmonische k-Formen: wenn eine Form in pVariablen holomorph und in q Variablen antiholomorph ist (mit p+q=k), dann bezeichnet man sie als (p,q)-Form. Entsprechend kann man die k-te Kohomologie zerlegen in die Summe der (p,q)-Kohomologien mit p+q=k. Die Dimension der (p,q)-Kohomologie heißt die (p,q)-Hodgezahl h^p,q.) Einige Beispiele von Hodge-Zahlen verschiedener Kähler-Mannigfaltigkeiten finden sich in diesem Wikipedia-Artikel (für 4-dimensionale Calabi-Yaus) oder in diesem (für die Quintik). Für die oben abgebildete Quintik sieht der "Hodge-Diamant" so aus:

			1
		0		0
	0		1		0
1		101		101		1
	0		1		0
		0		0
			1

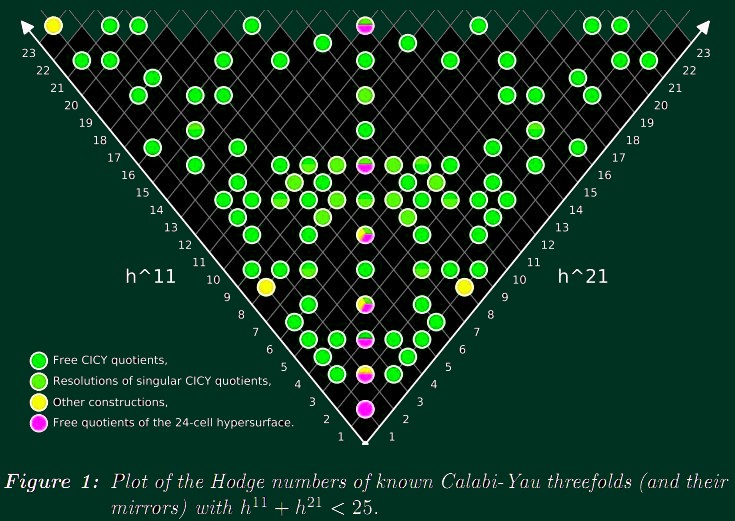
also h^1,1=1 und h^2,1=101. Alle bekannten Calabi-Yau-Mannigfaltigkeiten erfüllen h^1,1+h^2,1≤502. Eine Liste der jetzt bekannten Beispiele für die Werte von h^1,1 und h^2,1 zeigt das Bild unten aus motls.blogspot.com/2011/02/hodge-minimal-calabi-yau-three-fold.html: Die Frage, ob es Calabi-Yau-Mannigfaltigkeiten mit den minimal möglichen Hodge-Zahlen h^1,1=h^2,1=1 gibt, war bisher offen und sie scheint jetzt gelöst zu sein. Am Mittwoch erschien auf dem ArXiv der Preprint The 24-Cell and Calabi-Yau Threefolds with Hodge Numbers (1,1) von Volker Braun (Dublin), in dem drei verschiedene Calabi-Yau-Mannigfaltigkeiten mit jeweils h^1,1=h^2,1=1 konstruiert werd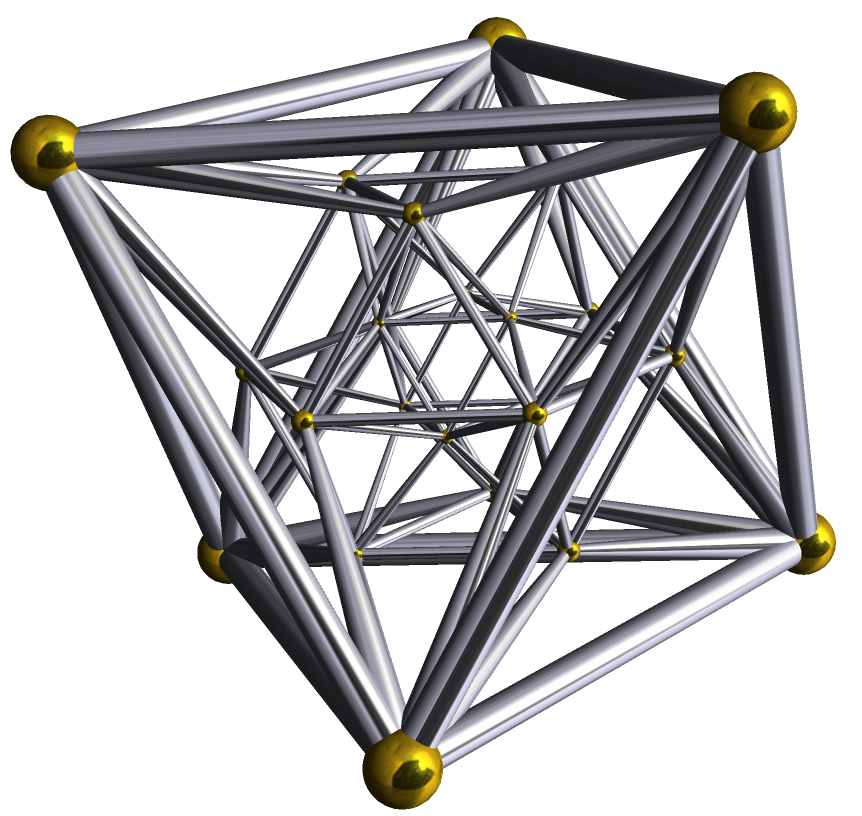en. Die Konstruktion benutzt eine Wirkung von SL(2,Z/3Z) auf dem 24-Zell (einem 4-dimensionalen Polytop, Bild oben) und die entsprechende Wirkung auf einer torischen Varietät. Ein Schnitt des antikanonischen Bündels über der torischen Varietät ist eine Calabi-Yau-Mannigfaltigkeit und deren Quotient bzgl. der SL(2,Z/3Z)-Wirkung hat die gewünschten minimalen Hodge-Zahlen.