Wie im
letzten Beitrag angekündigt heute also der KIAS-Wandkalender vom Mai, wieder in zwei Hälften:
Bei der
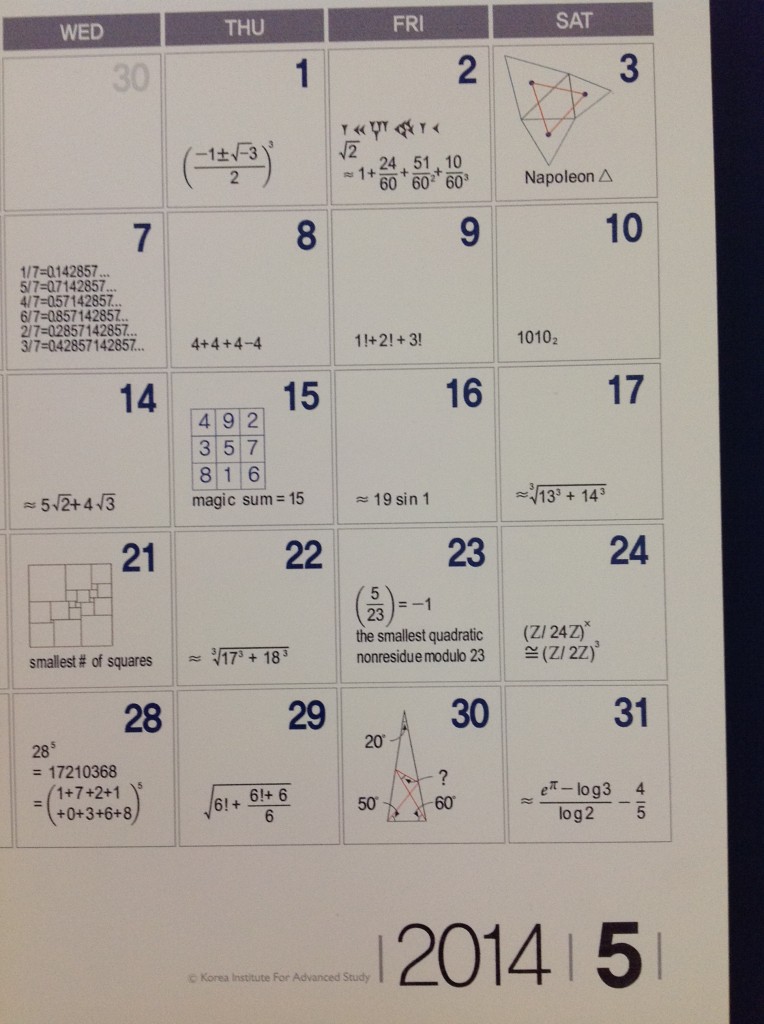
1 (Bild unten) geht es um kubische Einheitswurzeln: die Gleichung \(x^3=1\) hat neben \(x=1\) noch die beiden Lösungen \(x=\frac{-1\pm\sqrt{-3}}{2}\).
Der Eintrag bei der
2 zeigt eine
den Babyloniern vor 3700 Jahren bekannte Approximation der Quadratwurzel aus 2, der Eintrag bei der
3 das
Napoleon-Dreieck: die Schwerpunkte der nach außen aufgetragenen gleichseitigen Dreiecke bilden ihrerseits ein gleichseitiges Dreieck.
Der Eintrag bei der
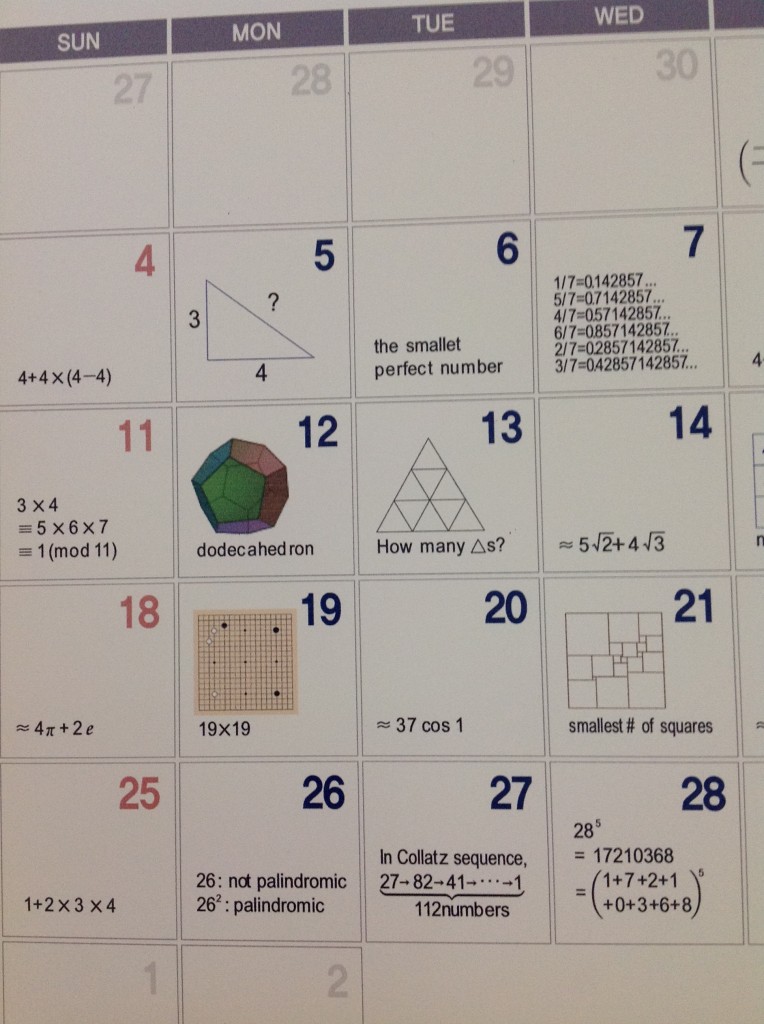
5 ist das kleinste
pythagoreische Tripel und die
6 die kleinste
vollkommene Zahl (so nennt man Zahlen, die gleich der Summe ihrer echten Teiler sind).
Der Eintrag bei der
17 ist kein Gegenbeispiel zur
Fermatschen Vermutung (ebensowenig wie der bei
22),
Go (das auf Koreanisch übrigens "Baduk" heißt) wird auf einem
19x19-Brett gespielt, der Eintrag bei der
21 zeigt das kleinste Quadrat, welches in Quadrate ganzzahliger Kantenlänge zerlegt werden kann (
"squaring the square") und der Eintrag bei
23 bedeutet, dass die Gleichung \(x^2\equiv 5\ mod\ 23\) keine Lösung besitzt (siehe
Legendre-Symbol).
Bei der
24 geht es um die
Einheitengruppe des Rings \({\mathbb Z}/24{\mathbb Z}\), also die Gruppe der invertierbaren Reste modulo 24: diese hat 8 Elemente, die (bis auf die 1) alle Ordnung 2 haben. Das Quadrat von
26 ist ein Palindrom, nämlich 676 und bei der
27 kommt der Collatz-Algorithmus erst nach 112 Schritten bei der 1 an. (Über die Collatz-Folgen und die 3n+1-Vermutung hatten wir
hier mal geschrieben.)
 Bei der 1 (Bild unten) geht es um kubische Einheitswurzeln: die Gleichung \(x^3=1\) hat neben \(x=1\) noch die beiden Lösungen \(x=\frac{-1\pm\sqrt{-3}}{2}\).
Der Eintrag bei der 2 zeigt eine den Babyloniern vor 3700 Jahren bekannte Approximation der Quadratwurzel aus 2, der Eintrag bei der 3 das Napoleon-Dreieck: die Schwerpunkte der nach außen aufgetragenen gleichseitigen Dreiecke bilden ihrerseits ein gleichseitiges Dreieck.
Der Eintrag bei der 5 ist das kleinste pythagoreische Tripel und die 6 die kleinste vollkommene Zahl (so nennt man Zahlen, die gleich der Summe ihrer echten Teiler sind).
Der Eintrag bei der 17 ist kein Gegenbeispiel zur Fermatschen Vermutung (ebensowenig wie der bei 22), Go (das auf Koreanisch übrigens "Baduk" heißt) wird auf einem 19x19-Brett gespielt, der Eintrag bei der 21 zeigt das kleinste Quadrat, welches in Quadrate ganzzahliger Kantenlänge zerlegt werden kann ("squaring the square") und der Eintrag bei 23 bedeutet, dass die Gleichung \(x^2\equiv 5\ mod\ 23\) keine Lösung besitzt (siehe Legendre-Symbol).
Bei der 24 geht es um die Einheitengruppe des Rings \({\mathbb Z}/24{\mathbb Z}\), also die Gruppe der invertierbaren Reste modulo 24: diese hat 8 Elemente, die (bis auf die 1) alle Ordnung 2 haben. Das Quadrat von 26 ist ein Palindrom, nämlich 676 und bei der 27 kommt der Collatz-Algorithmus erst nach 112 Schritten bei der 1 an. (Über die Collatz-Folgen und die 3n+1-Vermutung hatten wir hier mal geschrieben.)
Bei der 1 (Bild unten) geht es um kubische Einheitswurzeln: die Gleichung \(x^3=1\) hat neben \(x=1\) noch die beiden Lösungen \(x=\frac{-1\pm\sqrt{-3}}{2}\).
Der Eintrag bei der 2 zeigt eine den Babyloniern vor 3700 Jahren bekannte Approximation der Quadratwurzel aus 2, der Eintrag bei der 3 das Napoleon-Dreieck: die Schwerpunkte der nach außen aufgetragenen gleichseitigen Dreiecke bilden ihrerseits ein gleichseitiges Dreieck.
Der Eintrag bei der 5 ist das kleinste pythagoreische Tripel und die 6 die kleinste vollkommene Zahl (so nennt man Zahlen, die gleich der Summe ihrer echten Teiler sind).
Der Eintrag bei der 17 ist kein Gegenbeispiel zur Fermatschen Vermutung (ebensowenig wie der bei 22), Go (das auf Koreanisch übrigens "Baduk" heißt) wird auf einem 19x19-Brett gespielt, der Eintrag bei der 21 zeigt das kleinste Quadrat, welches in Quadrate ganzzahliger Kantenlänge zerlegt werden kann ("squaring the square") und der Eintrag bei 23 bedeutet, dass die Gleichung \(x^2\equiv 5\ mod\ 23\) keine Lösung besitzt (siehe Legendre-Symbol).
Bei der 24 geht es um die Einheitengruppe des Rings \({\mathbb Z}/24{\mathbb Z}\), also die Gruppe der invertierbaren Reste modulo 24: diese hat 8 Elemente, die (bis auf die 1) alle Ordnung 2 haben. Das Quadrat von 26 ist ein Palindrom, nämlich 676 und bei der 27 kommt der Collatz-Algorithmus erst nach 112 Schritten bei der 1 an. (Über die Collatz-Folgen und die 3n+1-Vermutung hatten wir hier mal geschrieben.)

