1 - 2 + 3 - 4 + - ... = 1/4 (Eulers paradoxe Gleichung) ist einer der Einträge im aktuellen Kalenderblatt. (Die Bilder lassen sich durch Anklicken vergrößern.) Die Formel bei der 2 ergibt sich per vollständiger Induktion aus der Gleichung \(\cos(\frac{x}{2})=\sqrt{\frac{\cos(x)+1}{2}} \). Es gibt nur 3 regelmäßige Pflasterungen der euklidischen Ebene, nämlich durch gleichseitige Dreiecke, Quadrate und regelmäße Sechsecke. 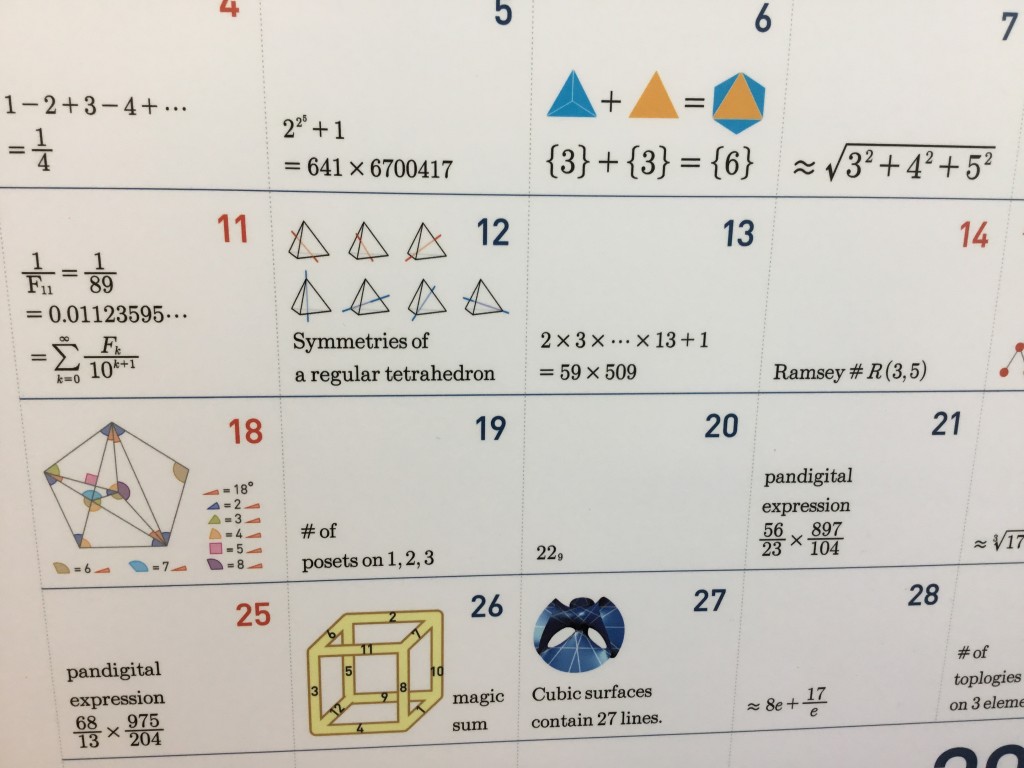(Viel mehr regelmäßige Pflasterungen hat man in der hyperbolischen Geometrie, siehe TvF 59.) Die 4 (Bild unten) zeigt die Reihe 1-2+3-4+-..., welche ein Spezialfall der Reihe \(1-2x+3x^2-4x^3+-\ldots=\frac{1}{(1+x)^2} \) ist, aus der man durch Einsetzen von x=1 das Ergebnis \(1-2+3-4+-\ldots=\frac{1}{4} \) erhält. Die englische Wikipedia hat zu dieser Reihe einen eigenen Artikel. Die 5 zeigt Eulers Gegenbeispiel zu einer Vermutung von Fermat, dass alle Zahlen der Form \(2^{2^n}+1 \) Primzahlen sind. Das Symbol bei der 8 finde ich nicht einmal mit Detexify. Die 11 zeigt eine Identität für Fibonacci-Zahlen, die ich vor 2 Jahren mal im Jahresendrätsel gestellt hatte. (Ebenso wie den Eintrag bei der 2 übrigens, die Auflösungen sind hier.) Jeder rot und blau kantengefärbte vollständige Graph auf 14 Knoten hat mindestens einen vollständig roten Teilgraphen auf 3 Knoten oder vollständig blauen Teilgraphen auf 5 Knoten. Ähnlich bei der 23. Ein pandigitaler Ausdruck wie bei der 21 oder 25 ist einer, der jede der 10 Ziffern genau einmal verwendet. Es gibt 8 invertierbare Elemente modulo 24. Magische Summen kennt man sonst aus magischen Quadraten. Bei der 26 geht es aber um einen Würfel, dessen Seitenflächen alle dieselbe Kantensumme haben. Die 27 Geraden auf einer kubischen Fläche sind ein beliebtes Thema für Bachelor- und Master-Arbeiten. Die Bernoulli-Zahlen B₄ und B₈ sind beide 30. Warum man das gerade auf diese Weise mit dieser Gleichung ausdrückt verstehe ich nicht.