Eine Arbeit von Altschuler und Philipps, veröffentlicht in Musical Times und populärwissenschaftlich aufbereitet in der Feature Column der AMS (Teil 1, Teil 2) interpretiert Musikwerke mittels der Topologie von Flächen. Für ein 2-dimensionales Koordinatensystem hat man die Zeit und die Tonhöhe - so ergibt jedes Musikstück einen Graphen in der 2-dimensionalen Ebene. Doch manchmal kommen zusätzliche Besonderheiten ins Spiel, wegen derer man statt der Ebene besser kompliziertere Flächen betrachten sollte. Die Autorem wenden das auf zwei der vierzehn Bachschen Kanons (BVW 1087) an, nämlich auf Kanon 3 (im Video ab 3:05) und Kanon 5 (im Video ab 4:28). 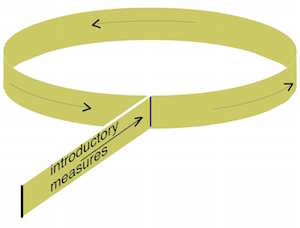https://youtu.be/6h6AabkLvEE Kanon 3 hat wie alle Bachschen Kanons die Struktur, dass das Stück nach einer Einleitung periodisch wird, also sich dann auf einem Zylinder bewegt: Kanon 5 hingegen hat die Besonderheit, dass das Notenbild eine Gleitspiegelung aufweist: Man bewegt sich also auf einem Möbiusband: Den selben Effekt hatte man auch beim Krabbenkanon: https://youtu.be/xUHQ2ybTejU Und wenn man noch die Tonalität berücksichtigt, also dass das hohe und das tiefe C in gewisser Weise derselbe Ton sind, dann bewegen sich die Musikstücke natürlich nicht mehr auf einem Zylinder oder Möbiusband, sondern auf einem Torus oder einer Kleinschen Flasche: 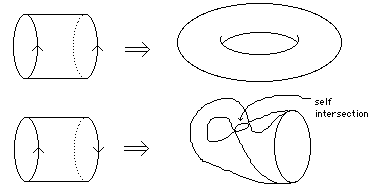Berechnen kann man damit natürlich nichts, es dient nur der Visualisierung.