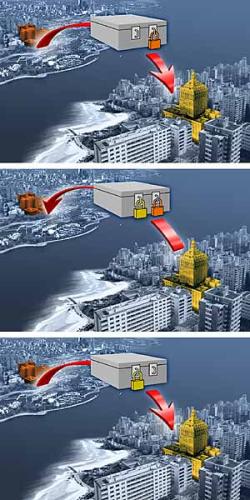
Alice will eine verschlossene Kiste mit einer Nachricht, aber ohne Schlüssel versenden. Dafür sichert sie die Kiste mit einem Vorhängeschloß, behält den Schlüssel, und schickt Bob die verschlossene Kiste. Bob kann die Kiste zwar nicht öffnen, aber sichert sie mit einem zweiten Vorhängeschloß, behält ebenfalls den Schlüssel, und schickt die doppelt gesicherte Kiste zurück zu Alice. Alice öffnet ihr Schloß mit ihrem Schlüssel, schickt die immer noch mit Bob's Vorhängeschloß gesicherte Kiste wieder an Bob und der kann sie jetzt mit seinem eigenen Schlüssel öffnen. Quelle So funktionieren heutige Verschlüsselungsverfahren, wie das auf der Unmöglichkeit einer effektiven Primzahlzerlegung beruhende RSA. Wenn man als Kunde eine Online-Verbindung zu einem Online-Kaufhaus herstellt, erstellt der Kaufhaus-Computer zwei zufällige große Primzahlen, erzeugt aus ihnen einen geheimen und einen öffentlicher Schlüssel, und sendet den öffentlichen Schlüssel und das Produkt der beiden Primzahlen an den Computer des Kunden. Er behält den geheimen Schlüssel und das Produkt der beiden Primzahlen, die Primzahlen selbst werden “vernichtet”. Mit dem öffentlichen Schlüssel erfolgt dann (ebenfalls automatisch ohne Zutun des Kunden) der Schlüsselaustausch zwischen Kundencomputer und Kaufhauscomputer. Und mit den ausgetauschten Schlüsseln wiederum läuft dann das AES-Verfahren, das die eigentlichen Daten (Kreditkartennummer etc.) verschlüsselt. Für die Sicherheit dieses Schlüsselaustausches ist es natürlich essentiell, dass es keine guten Algorithmen zur Faktorisierung großer Zahlen in Primzahlen gibt. Sehr viel einfacher als die Primfaktorzerlegung ganzer Zahlen zu finden ist die Zerlegung von Polynomen in "irreduzible" (unzerlegbare) Polynome - für diese gibt es in polynomieller Zeit arbeitende Algorithmen. Nun kann man ganze Zahlen auf vielerlei Weise als spezielle Werte von Polynomen darstellen. Zum Beispiel ist 513 der Wert von 5x²+x+3 an der Stelle x=10 oder der Wert von x⁹+1 an der Stelle x=2. Wegen x⁹+1=(x+1)(x⁸-x⁷+...-x+1) bekommt man daraus sofort die Zerlegung 513=3x171 (und kann dann versuchen 171 weiter zu zerlegen). Das Problem ist natürlich, dass nicht jedes Polynom sich genauso faktorisieren läßt wie seine Werte an einzelnen Stellen. Zum Beispiel wird es im obigen Beispiel nicht gelingen, das Polynom 5x²+x+3 in Faktoren zu zerlegen. Das Polynom ist irreduzibel, obwohl sich sein Wert bei x=10 ja weiter in Primfaktoren zerlegen ließ. (Und auch wenn sich jedes Polynom zerlegen ließe, wäre das kein wirklich praktikables Verfahren.) Aber trotzdem ist es ja eine zumindest theoretisch interessante Frage, ob solch ein Verfahren im Grundsatz funktionieren könnte, also ob die meisten Polynome sich faktorisieren lassen (in Polynome mit ganzzahligen Koeffizienten). Eine im Oktober auf dem ArXiv erschienene Arbeit von Emmanuel Breuillard und Peter Varju zeigt, dass das nicht der Fall ist: für Polynome mit Koeffizienten 0 und 1 und großem Grad (d.h. großem höchstem Exponenten) geht die Wahrscheinlichkeit, sich nicht zerlegen zu lassen, gegen 1. Ihr Beweis benutzt allerdings als Voraussetzung die noch unbewiesene Riemann-Vermutung für bestimmte Zahlkörper, nämlich für Q und Q(a), wobei a eine Nullstelle des Polynoms ist. Die Riemann-Vermutung besagt, dass für die Zetafunktion dieser Körper die Nullstellen auf der Geraden 1/2+iR liegen. Die Zetafunktion ist definiert durch analytische Fortsetzung der für Re(s)>1 durch die Summe der Werte 1/N(p)^s über alle Primideale p des Ganzheitsringes von Q(a) definierten konvergenten Reihe. N(p) ist die Norm des Ideals. Unter dieser Voraussetzung beweisen Breuillard und Varju dann, dass für eine Wahrscheinlichkeit 1-o(d) das Polynom ein Produkt eines irreduziblen Polynoms mit Polynomen der Form x^m und zyklotomischen Polynomen ist. Der Beweis läßt sich mittels Reduktion des Polynoms modulo einer Primzahl p darauf zurückführen, das Mischungsverhalten von Irrfahrten in der endlichen Gruppe Z/pZ zu untersuchen. Sie betrachten die Irrfahrt, die sich im j-ten Schritt um A_ja_j bewegt. (A_j sind die Koeffizienten und a_j die Nullstellen des zufällig gewählten Polynoms.) Sie berechnen, dass für einen festen Startwert a, die Wahrscheinlichkeit am Ende in 0 zu landen, ungefähr 1/p ist. Man landet aber gerade dann in 0, wenn a eine Nullstelle ist, und damit ist die Wahrscheinlichkeit für a eine Nullstelle zu sein ebenfalls ungefähr 1/p. Der Erwartungswert für die Anzahl der Nullstellen ist also 1. Aus Sätzen der analytischen Zahlentheorie folgt aber, dass in Z/pZ für eine geeignete Randomisierung der Erwartungswert für die Anzahl der Wurzeln zufällig gewählter Polynome gegen den Erwartungswert für die Anzahl irreduzibler Faktoren konvergiert. Also hat man mit hoher Wahrscheinlichkeit nur einen irreduziblen Faktor, d.h. Unzerlegbarkeit. Emmanuel Breuillard, Péter P. Varjú (2018). Irreducibility of random polynomials of large degree ArXiv Link