"Fläche mit einem dünnen Elektrizität leitenden Material bedeckt. Stationärer Strom auf der Fläche durch Verbindung zweier mit beliebigen Punkten der Fläche verbundenen Pole elektrischer Batterien. Das Potential des Stroms ist die Lösung eines Randwertproblems, das man aus einem Variationsproblem erhält. Suche unter allen möglichen Flüssen den mit der geringsten Wärme. Aus der Existenz der minimalen Funktion folgen die Existenzsätze der Funktionentheorie." So begründete Felix Klein in einem seiner Lehrbücher physikalisch die Existenz von Lösungen der Gleichung \(\frac{\partial^2f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}=0 \) auf einem Gebiet D, mit vorgegebenen Randwerten der Funktion f auf dem Rand des Gebietes D. Wenn man den Rand als eine Spule auffaßt, durch den ein Strom fließt, dessen Stromstärke den gegebenen Randwerten entspricht, dann bildet sich ein elektrisches Potential aus, das gerade eine Lösung dieser Gleichung ist. Mathematiker (einschließlich Klein selbst) waren mit solchen physikalischen Argumenten nicht zufrieden. Explizite Lösung für die Kreisscheibe und andere Gebiete mit glattem Rand gehen auf George Green zurück. Bernhard Riemann hatte das Problem umformuliert, indem er zeigte, dass die Lösungen der Gleichung sich als Minima eines bestimmten Funktionals ergeben. Weil das Funktional nur positive Werte annimmt, bewies das für ihn die Existenz einer Lösung, was er für den Beweis des Riemannschen Abbildungssatzes benutzte. Karl Weierstraß fand dann aber Beispiele (anderer) Funktionale, die nur positive Werte annehmen und trotzdem kein Minimum haben. David Hilbert bewies schließlich am Ende des 19. Jahrhunderts, dass (unter milden Voraussetzungen an den Rand) dieses spezielle Funktional immer ein Minimum und die Gleichung \(\frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2}=0 \) zu vorgegebenen Randwerten immer eine Lösung hat. Beispiele harmonischer Funktionen sind natürlich lineare Funktionen ax+by+c und viel allgemeiner Real- und Imaginärteile holomorpher Funktionen. So sind e^xcos(y) und e^xsin(y) als Real- und Imaginärteil der holomorphen Funktion e^z jeweils harmonische Funktionen. Das Maximumprinzip (Satz von Liouville) besagt, dass harmonische Funktionen auf kompakten Gebieten ihr Maximum auf dem Rand annehmen. Insbesondere gibt es keine nicht-konstanten, beschränkten, harmonischen Funktionen auf der Ebene.

Harmonische Funktionen auf Riemannschen Mannigfaltigkeiten

Den Operator \(\Delta f= \frac{\partial^2f}{\partial x^2}+\frac{\partial^2f}{\partial y^2} \) kann man auch interpretieren als \(\Delta f= - div(grad f) \) und diese Definition läßt sich verallgemeinern auf Riemannsche Mannigfaltigkeiten. Beispielsweise kann man für die hyperbolische Ebene dann zu jeder vorgegebenen Funktion auf dem Rand im Unendlichen eine harmonische Funktion finden, deren Grenzwerte im Unendlichen gerade die vorgegebene Funktion sind. Insbesondere findet man auf der hyperbolischen Ebene viele beschränkte, harmonische Funktionen. Dieser Unterschied zwischen euklidischer und hyperbolischer Ebene manifestiert sich auch im Allgemeinen: auf einfach zusammenhängenden Mannigfaltigkeiten negativer Krümmung gibt es nicht-konstante, beschränkte, harmonische Funktionen, während es auf einfach zusammenhängenden Mannigfaltigkeiten nichtnegativer Krümmung solche Funktionen nicht gibt.

Wachstum der Fundamentalgruppe und harmonische Funktionen

Seit den 70er Jahren betrachtet man in der Geometrie Eigenschaften, die nur von der "Grob-Geometrie" eines Raumes abhängen, die aber doch oft zumindest qualitativ Einfluß auf die Analysis auf dem Raum haben. So ist die universelle Überlagerung einer kompakten Mannigfaltigkeit quasi-isometrisch zur Fundamentalgruppe, womit qualitative Eigenschaften oft nur von der Fundamentalgruppe abhängen. Beispielsweise ist das Volumenwachstum in der universellen Überlagerung asymptotisch dasselbe wie das Wachstum der Fundamentalgruppe. 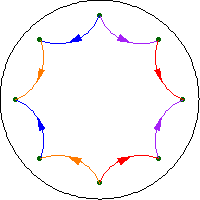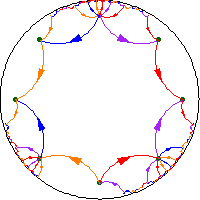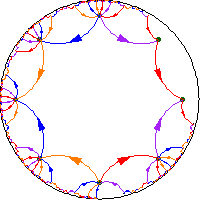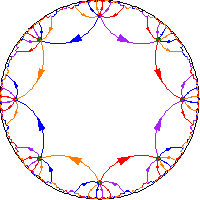Für eine negativ gekrümmte (einfach zusammenhängende) Mannigfaltigkeit ist das Volumenwachstum exponentiell, während für eine flache oder nichtnegativ gekrümmte Mannigfaltigkeit das Volumenwachstum polynomiell ist. In TvF 87 hatten wir mal über den Zusammenhang zwischen dem Wachstum der Fundamentalgruppe und der Rückkehrwahrscheinlichkeit von Irrfahrten geschrieben. Und auch die Existenz beschränkter harmonischer Funktionen hängt eng mit den Eigenschaften der Fundamentalgruppe zusammen. Mitte der 80er Jahre bewiesen zunächst Lyons und Sullivan, dass es bei polynomiellem Wachstum der Fundamentalgruppe keine nicht-konstanten, beschränkten, harmonischen Funktionen geben kann. Kaimanowitsch verbesserte das dann noch auf subexponentielles Wachstum. (Damit bekommt man zum Beispiel universelle Überlagerungen von Mannigfaltigkeiten nichtnegativer Krümmung.) Umgekehrt wußte man bisher (aus der Arbeit von Lyons und Sullivan), dass es bei nicht-mittelbaren Fundamentalgruppen stets nicht-konstante, beschränkte, harmonische Funktionen gibt. (Damit bekommt man zum Beispiel universelle Überlagerungen von Mannigfaltigkeiten negativer Krümmung.) Dieses Resultat wird nun in einem letzte Woche erschienenen Preprint von P. Polymerakis (MPI Bonn) verbessert: bei exponentiellem Wachstum der Fundamentalgruppe gibt es stets nicht-konstante, positive, harmonische Funktionen. Das bestätigt die entsprechende 1984 von Lyons und Sullivan aufgestellte Vermutung. Panagiotis Polymerakis. (2019) Positive harmonic functions on covering spaces. arXiv: 1906.11723v1