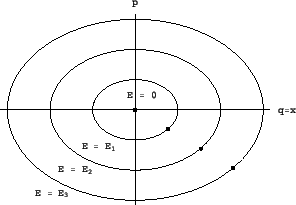
Stabilitätstheorie von Differentialgleichungen fragt, wie die Störung der Anfangswerte eines Systems sich auf die weitere Entwicklung auswirkt, beispielsweise ob in einer Umgebung eines Gleichgewichtspunktes von x'=f(x) die Bahnen in einer (eventuell etwas größeren) Umgebung des Gleichgewichtspunktes verbleiben oder sogar gegen den Gleichgewichtspunkt konvergieren. Im ersten Fall spricht man von einem stabilen Gleichgewicht, im zweiten von einem asymptotisch stabilen Gleichgewicht. Zwei Beispiele: Der harmonische Oszillator, also das Differentialgleichungssystem x‘=v mv‘+kx=0 hat einen Gleichgewichtspunkt in (0,0). Weil die Energie mv2/2+kx2/2 konstant ist, bewegen sich die Bahnen auf Ellipsen um den Gleichgewichtspunkt, woraus die Stabilität des Gleichgewichts folgt.
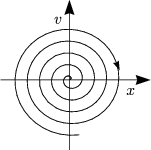
Für den gedämpften Oszillator, der durch das Differentialgleichungssystem x‘=v mv‘+2mγx‘+kx=0 beschrieben wird, ist (0,0) ebenfalls ein Gleichgewichtspunkt und für γ>0 nimmt die Energie monoton ab. Daraus folgt, dass alle Bahnen in das Minimum der Energie, also in den Gleichgewichtspunkt (0,0) streben. Der Gleichgewichtspunkt ist also asymptotisch stabil.
Im 19. Jahrhundert benutzte man meist Linearisierungen im Gleichgewichtspunkt, um Stabilität zu untersuchen. (Im Stile des Satzes von Hartman-Grobman, der in seiner Allgemeinheit freilich erst viel später bewiesen wurde.) Erst Ljapunow in seiner 1892 eingereichten Habilitationsschrift Общая задача об устойчивости движения hatte die eigentlich sehr einfache Idee, dass man statt der Energiefunktion auch beliebige andere Funktionen V betrachten kann, solange sie im Gleichgewichtspunkt ein striktes Minumum haben und entlang der Bahnen abnehmen. Er bewies Stabilität, falls V‘≤0 entlang Bahnen, und asymptotische Stabilität, falls V‘<0 entlang der Bahnen.
Ljapunow hatte in seiner Habilitationsschrift zwei unterschiedliche Methoden zur Untersuchung von Stabilitätsfragen entwickelt, neben den Ljapunowfunktionen noch den Ljapunowexponenten
\(L(x)=\lim_{t\to\infty}\log\vert \frac{d\Phi(x,t)}{dt}\vert \) für den Fluß Φ(x,t) einer gewöhnlichen Differentialgleichung. Ein Gleichgewichtspunkt x0 ist stabil, wenn L(x0)≤0, und asymptotisch stabil, wenn L(x0)<0.
Ljapunows Arbeit wurde erst 16 Jahre später ins Französische (und erst zum hundertjährigen Jubiläum ins Englische) übersetzt und es dauerte lange, bis sie im Westen größere Aufmerksamkeit fand. Ljapunow selbst hatte den Ljapunowexponenten für das wichtigere der beiden Konzepte gehalten, tatsächlich wurde dann aber die Verwendung von Ljapunowfunktionen zur Standardmethode in der Stabilitätstheorie. Erst mit dem 1965 von Oseledez bewiesenen multiplikativen Ergodensatz wurde auch der Ljapunowexponent revitalisiert. Bild: https://commons.wikimedia.org/wiki/File:Alexander_Ljapunow_jung.jpg