In Émile Borels 1894 eingereichter Dissertation „Sur quelques points de la théorie des fonctions“ ging es eigentlich um eine Verallgemeinerung der Methode der analytischen Fortsetzung. Als Hilfsmittel bewies er dabei aber auch einen Satz, von dem er meinte, dass er „von unabhängigem Interesse“ sein dürfte: wenn man das abgeschlossene Intervall [a,b] durch (unendlich viele) offene Intervalle überdeckt, dann kann man endlich viele dieser Intervalle auswählen, die bereits ganz [a,b] überdecken. Borel bewies eigentlich einen etwas schwächeren Satz: Jede abzählbare Überdeckung eines abgeschlossenen Intervalls durch offene Mengen hat bereits eine endliche Teilüberdeckung. Die Abzählbarkeit ist hier aber nicht notwendig. Heute bezeichnet man als Satz von Heine-Borel meist folgende Verallgemeinerung: eine Teilmenge des Rⁿ ist genau dann abgeschlossen und beschränkt, wenn jede Überdeckung durch offene Mengen bereits eine endliche Teilüberdeckung hat. 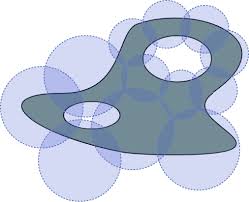Das Bild oben zeigt eine offene Überdeckung einer abgeschlossenen und beschränkten Menge. Im Bild besteht diese offene Überdeckung bereits aus endlich vielen Mengen, die Folgerung des Satzes ist also trivialerweise erfüllt. Ein nichttriviales Beispiel, wie man den Satz typischerweise anwendet, besteht darin, dass man um jeden Punkt der Menge eine offene Kugel betrachtet. Das ist eine (unendliche) offene Überdeckung der Menge. Egal wie groß (oder klein) die Radien der Kugeln gewählt werden, der Satz besagt, dass man immer endlich viele Kugeln auswählen kann, die bereits die ganze Menge überdecken. Implizit war dieser Satz sowohl von Heine als auch von Dirichlet und Weierstraß bereits verwendet worden. (Heine und auch schon Dirichlet hatten damit die gleichmäßige Stetigkeit stetiger Funktionen auf abgeschlossenen Intervallen bewiesen.) Borel war aber der erste, der ihn formulierte und bewies (für abzählbare Überdeckungen). Fast gleichzeitig mit Borel bewies Pierre Cousin in einer ebenfalls funktionentheoretischen Arbeit im Wesentlichen denselben Satz (für Teilmengen der Ebene und nicht notwendig abzählbare Überdeckungen). Den heute üblichen Beweis (für Intervalle) fand Lebesgue 1904: er betrachtete zu einem mit offenen Intervallen überdeckten Intervall [a,b] die Menge der Punkte x, für die es keine endliche Menge an offenen Intervallen gibt, welche [a,x] bereits überdecken. Diese Menge hat eine größte untere Schranke x₀. Dieser Punkt liegt aber in einem offenen Intervall, so dass man einen Widerspruch zur Maximalität von x₀ bekommt. Mengen, die die Schlußfolgerung des Überdeckungssatzes erfüllen, bezeichnet man heute als kompakte Mengen. Einige der elementaren (im Sinne von für die Mathematik lebensnotwendigen) Anwendungen von Kompaktheit: - stetige Funktionen sind beschränkt und nehmen ihr Maximum und Minimum an, - alle Folgen haben Häufungspunkte, - und ganz allgemein kann man lokale Kontrolle in globale Kontrolle verwandeln. Ein Beispiel für letzteres Phänomen ist natürlich die gleichmäßige Stetigkeit stetiger Funktionen auf kompakten Mengen, bei deren Beweis sich das Konzept ursprünglich bei Dirichlet und Heine auf natürliche Weise ergeben hatte. Ein anderes typisches Beispiel ist, dass auf kompakten Mannigfaltigkeiten M die Lösungen einer gewöhnlichen Differentialgleichung für alle Zeiten existieren: nach den bekannten (lokalen) Existenz- und Eindeutigkeitssätzen hat man zu jedem Punkt x eine Umgebung U_x und ein kleines Zeitintervall (-ε_x,ε_x), auf dem eine eindeutige Lösung existiert. Die U_x bilden eine offene Überdeckung, also gibt es endlich viele, die M bereits überdecken. Zu den endlich vielen zu dieser Teilüberdeckung gehörenden ε_x gibt es ein positives Minimum, also eine positive Zahl, bis zu der die Lösung der Differentialgleichung überall existiert, woraus leicht die Existenz der Lösung für alle Zeiten folgt. https://youtu.be/Wmj9ZMHfHNw https://youtu.be/1qqp8XoGL-k