Ursprünglich motiviert von Fragestellungen, die aus der Analysis reeller Funktionen stammen (Ausnahmemengen für die Konvergenz von Fourier-Reihen) und später aus eher metaphysischen Motiven hatte Georg Cantor seit den 1870er Jahren die Theorie der Punktmengen und dann die abstrakte Mengenlehre entwickelt. Felix Hausdorff beschäftigte sich ursprünglich aus philosophischem Interesse mit Cantors Mengenlehre, sein 1914 erschienenes Hauptwerk "Grundzüge der Mengenlehre" war dann aber kein philosophisches, sondern ein mathematisches Buch. Es sollte die Idee befördern, dass viele Sätze über metrische Räume auch in allgemeineren topologischen Räumen richtig sind. Maurice Frechet hatte 1906 in seiner Dissertation bei Hadamard metrische Räume eingeführt (die aber erst von Hausdorff so genannt wurden) und topologische Begriffe wie Kompaktheit und Trennbarkeit definiert. Statt von einer Metrik ging Hausdorff in seinem Buch dann von einer Topologie aus, d.h. einer abstrakten Definition offener Umgebungen mit gewissen Eigenschaften: abzählbare Durchschnitte und beliebige Vereinigungen der von den offenen Umgebungen erzeugten offenen Mengen sollen wieder offen sein, weiter verlangte er ein Trennungsaxiom. Für metrische Räume definieren die offenen Mengen (also diejenigen, wo zu jedem Punkt eine offene metrische Kugel um den Punkt noch in der Menge liegt) eine solche Topologie. Die Rolle offener Umgebungen war kurz zuvor schon in einem Buch von Hermann Weyl über Riemannsche Flächen betont worden, und die Definition topologischer Räume über die Eigenschaften offener Mengen setzte sich letztlich durch, u.a. weil man in vielen Funktionenräumen zwar natürliche Topologien, aber keine kanonischen Metriken hat. Hausdorffs Definition topologischer Räume wurde später noch dahingehend modifiziert, dass man statt offener Umgebungen die offenen Mengen zur Grundlage der Theorie machte, außerdem verzichtete man auf das (später als Hausdorff-Eigenschaft bezeichnete) Trennungsaxiom. Zur Mengenlehre im damaligen Verständnis zählten auch die Theorie der Punktmengen und die Maß- und Integrationstheorie. Auch wenn es ältere Behandlungen des Themas gab, wurde Hausdorffs Werk das Buch, von dem folgende Mathematikergenerationen - allerdings erst die neuen Generationen nach dem Krieg, der vier Monate nach Erscheinen des Buches begann - die Elemente der Mengenlehre und Punktmengentopologie lernen würden. Insbesondere seine einfache Definition von Zusammenhang - die schon andere vor ihm gefunden hatten - als die Unzerlegbarkeit eines Raumes in disjunkte offene Mengen setzte sich durch. Hausdorff benutzt zwar den Wohlordnungssatz, um zu beweisen, dass teilgeordnete Mengen maximale linear geordnete Untermengen enthalten. Sonst vermied er ihn aber weitgehend und bevorzugte transfinite Induktion. Den Übergang von endlicher zu abzählbarer Additivität in der neuen Maß- und Integrationstheorie bezeichnete er als einen der größten Fortschritte der Mathematik, aber das Auswahlaxiom wollte er doch lieber auf abzählbare Auswahlen eingeschränkt wissen. Nachdem Vitali schon 1905 gezeigt hatte, dass aus dem Auswahlaxiom die Existenz nicht-meßbarer Mengen folgt, entdeckte Hausdorff, dass man mit Hilfe des Auswahlaxioms eine Sphäre in Stücke zerlegen kann, die anders zusammengesetzt zwei Kugeln desselben Radius geben. Das wurde später als Banach-Tarski-Paradoxon bekannt. Die Stücke der Zerlegung können nicht meßbar sein, weil man andernfalls eine Verdoppelung des Volumens bewerkstelligt hätte. Wie die meisten Mathematiker setzte Hausdorff statt einer konsequenten Axiomatisierung auf eine pragmatische Mengenlehre, die Problem-Mengen mied. Nach und nach wurde es immer mehr Mathematikern bewusst, dass die Mengenlehre eine unentbehrliche Grundlage für die Strukturierung der Mathematik ist. Das von Zermelo (mit einem weiteren Axiom von Fraenkel) eingeführte System bewährte sich in der Praxis, weshalb es als Basis der modernen Mathematik von der Mehrheit der Mathematiker anerkannt wurde. Von Georg Cantor stammt auch die erste veröffentlichte rigorose Definition der reellen Zahlen als Vervollständigung (durch Grenzwerte von Cauchy-Folgen) der rationalen Zahlen. Im selben Jahr 1872 veröffentlichte auch Eduard Heine eine im Wesentlichen äquivalente Definition. Richard Dedekind hatte bereits 1858 seine Theorie der Dedekind-Schnitte ausgearbeitet, veröffentlichte sie aber erst 1872, als er von Cantors und Heines geplanten Veröffentlichungen erfuhr. 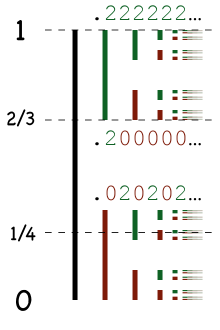Näher an der Intuition und der Schulmathematik ist es natürlich, reelle Zahlen als Dezimalbrüche einzuführen, was Simon Stevin schon 1585 vorgeschlagen hatte. Das Problem mit diesem Ansatz ist, dass unterschiedliche Dezimalbrüche dieselbe Zahl darstellen können: 0,999… ist dasselbe wie 1,000…, und genauso ist dann auch 0,02999… dasselbe wie 0,03 und 1,34999… dasselbe wie 1,35 und so weiter. Das mathematisch korrekt zu formulieren ist letztlich viel umständlicher als reelle Zahlen durch Dedekind-Schnitte oder Cauchy-Folgen zu definieren. Außerdem arbeiten Mathematiker ohnehin mit den Eigenschaften der reellen Zahlen und nicht mit ihrer formalen Definition. Eine neue Sichtweise auf diese Definition der reellen Zahlen wurde von Dustin Clausen und Peter Scholze in ihrer seit 2018 entwickelten „Verdichteten Mathematik“ aufgebracht. Dezimalbrüche ohne die Identifizierungen der Art 0,999…=1 bilden eine Cantor-Menge, also eine kompakte, total unzusammenhängende Menge. Durch die Identifizierungen wird aus der Cantor-Menge ein Kontinuum. Clausen und Scholze sind der Überzeugung, dass dieser Zugang der richtige Ansatz zu einem Neuaufbau der Topologie sei. Statt Hausdorffs klassischer Definition topologischer Räume wollen sie Räume – analog zur Konstruktion reeller Zahlen durch Dezimalbrüche – durch Verklebungen total unzusammenhängender Räume gewinnen. Formal definieren sie “verdichtete Mengen” (engl. “condensed sets”) als Garben auf total unzusammenhängenden Räumen (Stone-Räumen). Beispielsweise können sie so die reelle Funktionalanalysis mit Methoden der Zahlentheorie angehen. (Total unzusammenhängende Räume kamen bisher vor allem in der p-adischen Geometrie vor, einem Gebiet der Zahlentheorie.) Seit dem Ende des 20. Jahrhunderts sind Computerbeweise ein Thema der Mathematik. Dabei gab es einerseits Beweise wie beim Vierfarbenproblem oder der Kepler-Vermutung, wo mit Hilfe eines Computers viele einzelne Fälle abgearbeitet werden konnten, was für Menschen nicht machbar gewesen wäre. Andererseits gab es Formalisierungen bekannter Beweise, die dann mit dem Computer überprüft werden konnten. Der erste war 1986 ein Computerbeweis von Gödels Unvollständigkeitssatz. Es gab dann später auch Formalisierungen der Beweise des Vierfarbenproblem und der Kepler-Vermutung, oder beispielsweise zu Selbergs Beweis des Primzahlsatzes, zum Satz von Feit-Thompson, zum Jordanschen Kurvensatz und zum Brouwerschen Fixpunktsatz. Das meistverwendete Beweisassistent war zu dieser Zeit HOL Light, basierend auf einer Formulierung der Typentheorie. Vor allem Vladimir Voevodsky vertrat seit 2009, dass man Homotopietypentheorie, basierend auf dem Begriff der Modellkategorie, zur Überprüfung von Beweisen etwa in der Algebra verwenden sollte. Der ursprünglich seit 1989 auf Basis klassischer Typentheorie entwickelte Beweisassistent Coq wurde in diesem Sinne erweitert, konnte aber durchaus auch Sachen, die sich mit Voevodskys univalenter Mathematik nicht machen ließen. Die besten Ergebnisse sollte, wie etwa Kevin Buzzard in Vorträgen ab 2019 vertrat, der auf abhängiger Typentheorie basierende Beweisassistent Lean erreichen. Als Reaktion auf diese Debatte schlug Peter Scholze in Buzzards Blog 2020 eine Formalisierung seines nach seiner Aussage für die Algebraisierung der Analysis wichtigsten Theorems vor, einem Satz aus seiner Arbeit mit Dustin Clausen über verdichtete Mathematik, der unter dem Namen Liquid Tensor Experiment bekannt wurde und dann von Lean tatsächlich nach nur einem halben Jahr überprüft werden konnte:

Seien \(0\textless p^\prime\textless p\leq 1\) reelle Zahlen, sei S eine pro-endliche Menge, und sei V ein p-Banach-Raum. Sei \(\mathcal M_{p'}(S)\) der Raum der p'-Maße auf S. Dann ist \(\mathrm{Ext}^i_{\mathrm{Cond}(\mathrm{Ab})}(\mathcal M_{p'}(S),V)=0\) für \(i\geq 1\)

Hier noch einmal alle Artikel der Reihe: Die Klassifikation der einfachen Lie-Algebren. Der Wiederkehrsatz von Poincaré Minkowskis Gitterpunktsatz Ljapunow-Stabilität Hilberts Nullstellensatz Der Überdeckungssatz von Heine-Borel Poincaré-Dualität Der Primzahlsatz Hilberts Produktformel Komponierbarkeit quadratischer Formen Die Widerspruchsfreiheit der euklidischen Geometrie Das Runge-Kutta-Verfahren Lebesgues Satz über dominierte Konvergenz Fortsetzbarkeit von L-Funktionen Die Fredholm-Alternative Der Wohlordnungssatz Schurs Lemma Der Spektralsatz für beschränkte Operatoren Der Satz von Riesz-Fischer Das Ritz-Verfahren Borels Gesetz der großen Zahlen Der algebraische Abschluß von Körpern Invarianz der Dimension Der Abbildungssatz Der Satz vom höchsten Gewicht Die Klassifikation algebraischer Flächen Die Einstein-Hilbert-Wirkung Charakterisierung analytischer Mengen Multiplikativität der Ramanujanschen Tau-Funktion Das Noether-Theorem Kongruenzen der Partitionsfunktion Der Satz von Thue-Siegel Das Lokal-Global-Prinzip Der Banachsche Fixpunktsatz Die Lefschetzsche Fixpunktformel Der Fisher-Test Die Hauptsätze der Werteverteilungstheorie Der Satz von Peter-Weyl Das Artinsche Reziprozitätsgesetz Der Spektralsatz für unbeschränkte Operatoren Der Satz von Mordell-Weil Existenz unendlich vieler Geodätischer Der Ergodensatz Der Satz von Brauer-Hasse-Noether Das Fundamentallemma der mathematischen Statistik Pontrjagin-Dualität Der Satz von Tichonow Der Einbettungssatz von Whitney Der Satz von Winogradow Der Sobolewsche Einbettungssatz Der Satz von Teichmüller Die Riemann-Vermutung für Funktionenkörper Das Hodge-Theorem Siegel-Scheiben Stetiger Funktionalkalkül Der Satz von Chern-Gauß-Bonnet Der Eilenberg-Steenrod-Eindeutigkeitssatz Die Leray-Spektralsequenz Konditionierung linearer Gleichungssysteme Das Simplex-Verfahren Das WKS-Abtasttheorem Adelische Poisson-Summation Der Vergleichssatz von Rauch Die Berechnung des Kobordismusrings Die Endlichkeit der Homotopiegruppen von Sphären Der Einbettungssatz von Nash Serre-Dualität Die Selbergsche Spurformel Bott-Periodizität Der Satz von Grothendieck-Riemann-Roch Der Eichler-Shimura-Isomorphismus Der meßbare Riemannsche Abbildungssatz Der h-Kobordismus-Satz Der Satz von Feit-Thompson Der Atiyah-Singer-Indexsatz Auflösung der Singularitäten Das Prinzip der großen Abweichungen Lusins Vermutung Strukturelle Stabilität hyperbolischer Systeme Das Yoga der Motive Konvergente Differenzenschemata der Navier-Stokes-Gleichung Die Jacquet-Langlands-Korrespondenz NP-Vollständigkeit des SAT-Problems Dualität des BMO-Raums zum Hardy-Raum Die LBB-Bedingung Die Weil-Vermutungen Der Superstarrheitssatz Der Vier-Farben-Satz Die Calabi-Vermutung Thurstons Satz über hyperbolische Dehn-Chirurgie Irrationalität von Zeta(3) Shelahs Main Gap Die Kazhdan-Lusztig-Vermutungen Exotische vierdimensionale Räume Die Mordell-Vermutung Der Satz über wandernde Gebiete Lösung des Wortproblems für hyperbolische Gruppen Das Gaußsche Klassenzahlproblem Die Arnold-Vermutung für monotone symplektische Mannigfaltigkeiten Multiresolutionsanalyse von Wavelets Der Maßstarrheitssatz Die Witten-Vermutung Das eingeschränkte Burnside-Problem Monströser Mondschein Mirrorsymmetrie für Calabi-Yau-Hyperflächen in torischen Varietäten Die Thom-Vermutung Der große Satz von Fermat Die Milnor-Vermutung Das Scheffer-Shnirelman-Paradoxon Die Baum-Connes-Vermutung für kokompakte Gitter in SL(3) Vergleich der Regulatoren von Beilinson und Borel Das Skalierungslimit schleifenbereinigter Irrfahrten Die Langlands-Korrespondenz für Funktionenkörper Die Gromov-Witten-Invarianten der projektiven Gerade Die Poincaré-Vermutung Der Satz von Green-Tao Die Mirzakhani-McShane-Identitäten Die Arnold-Vermutung Serres Modularitätsvermutung Das Fundamentallemma Nichtlineare Landau-Dämpfung Eindeutige Quantenergodizität für SL(2,Z)\H Die Read-Vermutung Die Waldhausen-Vermutung Der Satz über beschränkte Primzahllücken Die Grunewald-Ash-Vermutung Die Yau-Tian-Donaldson-Vermutung Erdős’ Diskrepanz-Problem Optimalität der E8-Kugelpackung Die Hodge-Riemann-Relationen für Matroide Die Onsager-Vermutung Das Liquid Tensor Experiment