"What was that adjective? I liked that." The Volokh Conspiracy zitiert aus den Prozeßakten Briscoe & Cypress v. Virginia:

MR. FRIEDMAN: I think that issue is entirely orthogonal to the issue here because the Commonwealth is acknowledging -
CHIEF JUSTICE ROBERTS: I'm sorry. Entirely what?
MR. FRIEDMAN: Orthogonal. Right angle. Unrelated. Irrelevant.
CHIEF JUSTICE ROBERTS: Oh.
JUSTICE SCALIA: What was that adjective? I liked that.
MR. FRIEDMAN: Orthogonal.
CHIEF JUSTICE ROBERTS: Orthogonal.
MR. FRIEDMAN: Right, right.
JUSTICE SCALIA: Orthogonal, ooh.
(Laughter.)
JUSTICE KENNEDY: I knew this case presented us a problem.
(Laughter.)
MR. FRIEDMAN: I should have -- I probably should have said -
JUSTICE SCALIA: I think we should use that in the opinion.
(Laughter.)
MR. FRIEDMAN: I thought -- I thought I had seen it before.
JUSTICE SCALIA: Or the dissent.
(Laughter.)
MR. FRIEDMAN: That is a bit of professorship creeping in, I suppose.

(via God plays dice) Es geht übrigens um diese Petition zur Umsetzung der Confrontation Clause. Der Topologe Peter Shalen kommentiert auf The Volokh Conspiracy

Professor Friedman's use of "orthogonal" is correct. It's refreshing to see a mathematical term used correctly for a change. Recent years have brought us fashionable misuses of "lowest common denominator" and "parameters," and just the other day Tom Friedman misused "point of inflection."

In der Statistik werden unabhängige (unkorrelierte) Variablen manchmal als "orthogonal" bezeichnet. 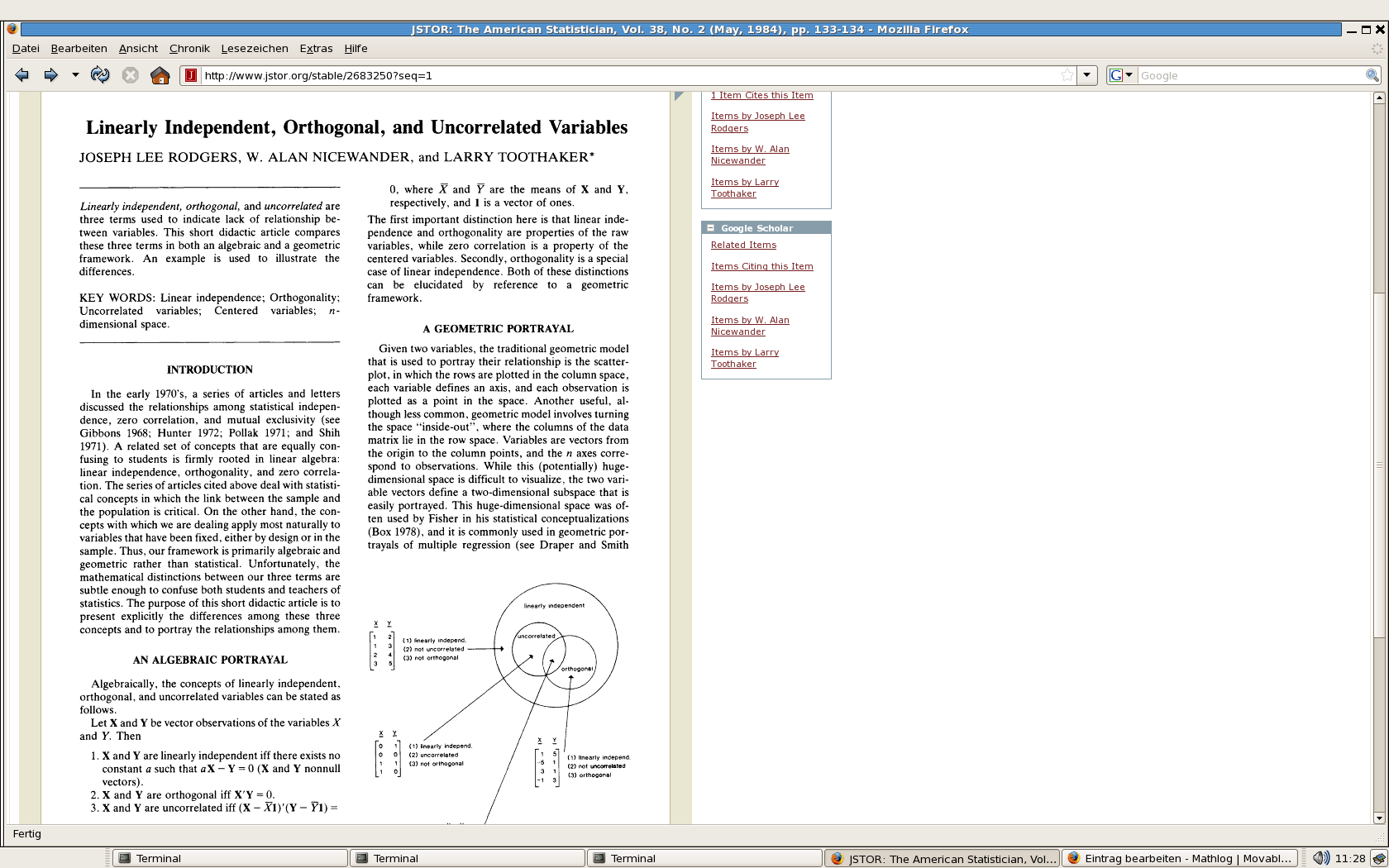https://www.jstor.org/pss/2683250?seq=1 Weiß jemand, warum unkorrelierte Variablen "orthogonal" genannt werden? Entsprechen unkorrelierte Variablen vielleicht orthogonalen Vektoren in irgendeinem Hilbertraum?