Im Mathematik-Test für die vor einigen Wochen veröffentlichte PISA-Studie gab es auch eine Aufgabe zur Geometrie metrischer Räume. Man findet die Aufgabenbeispiele hier (ganz unten), es handelt sich um Beispiel 6: Navigation. “Diese Aufgabe veranschaulicht mathematisches Argumentieren in einem geometrischen Kontext und die Möglichkeiten des computerbasierten Testens.“

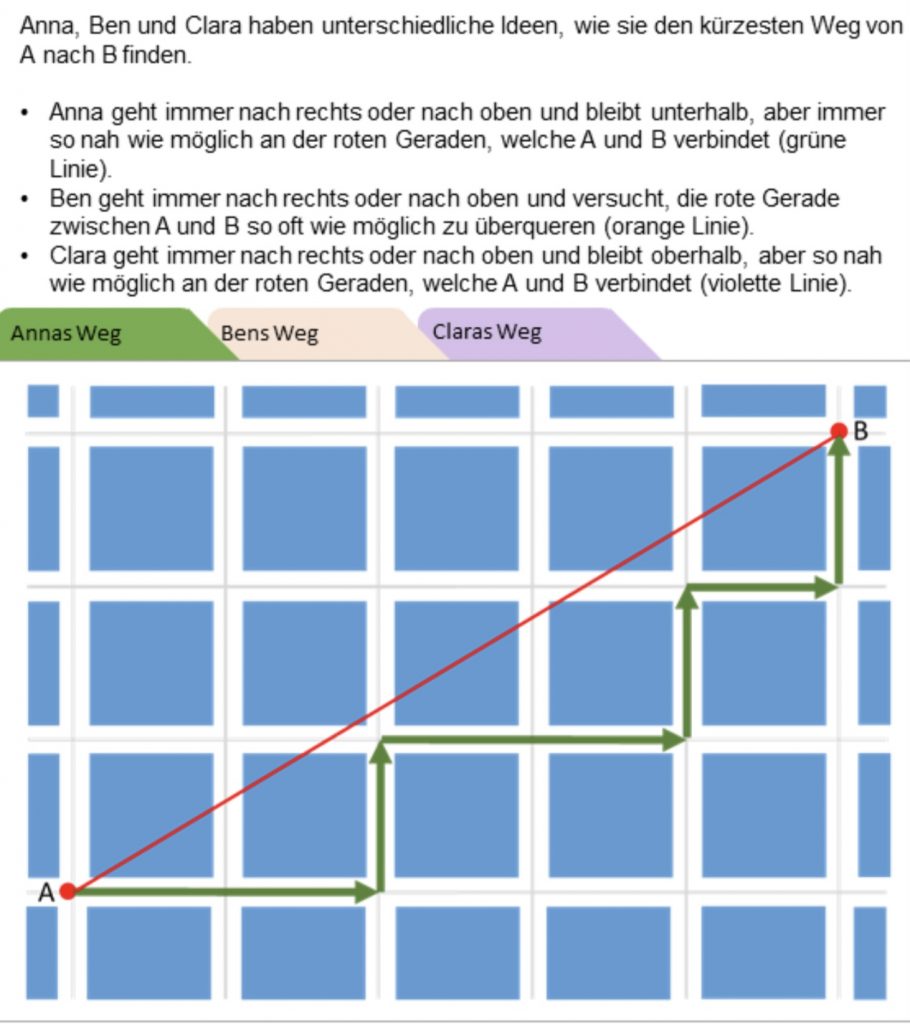
Man muss dann weiterklicken, um auch Bens und Claras Weg angezeigt zu bekommen.

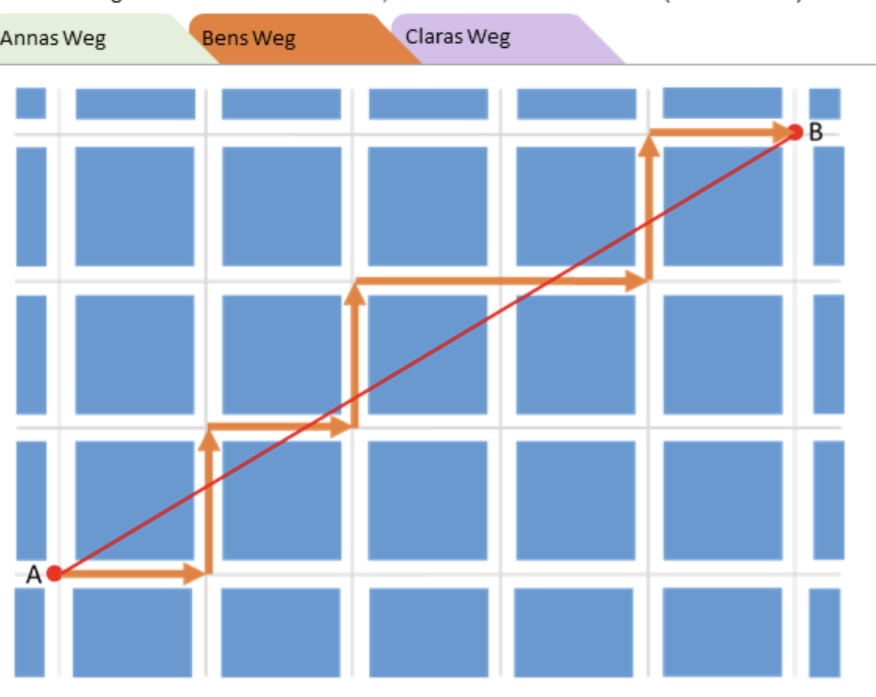
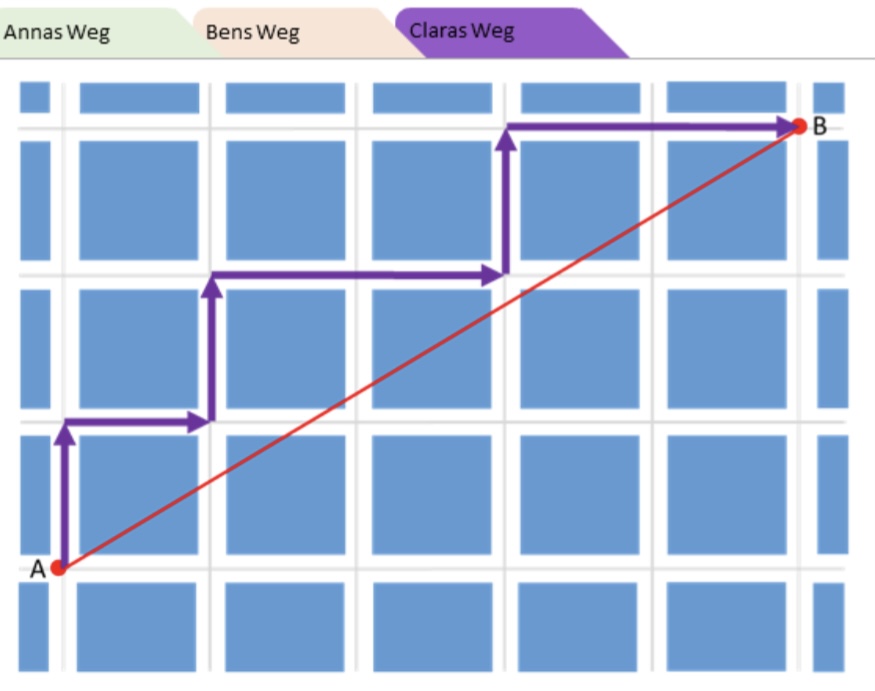
Mit Computerhilfe soll man dann feststellen, dass alle drei Wege gleich lang sind, und das soll man dann aber noch begründen.

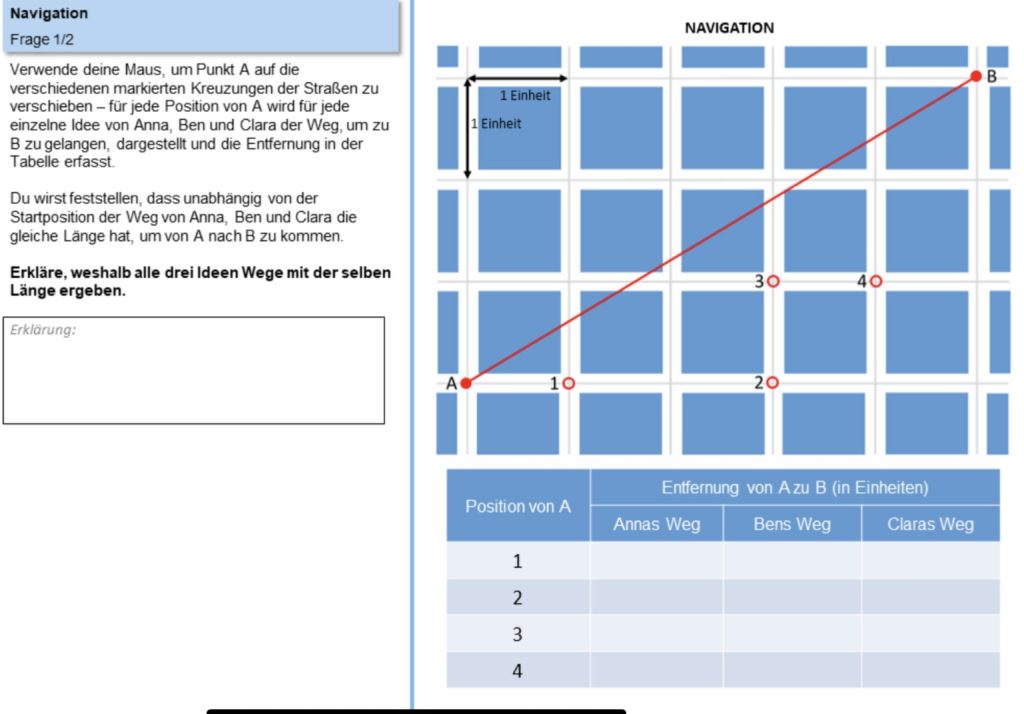
Schließlich soll man noch entscheiden, welche Diagonalen einen Weg abkürzen oder nicht.

Die zweidimensionale Ebene faßt man seit Descartes auf als die Menge der Zahlenpaare (x₁ , x_2.) Der Abstand zwischen zwei Punkten läßt sich nach dem Satz des Pythagoras berechnen als Quadratwurzel aus der Summe der Differenzquadrate..

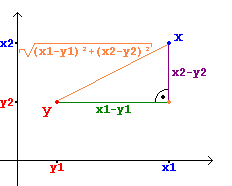
Dieser Abstand, der sogenannte euklidische Abstand, mißt also die Entfernung per Luftlinie zwischen zwei Punkten in einer flachen Ebene. Wenn man Abstände zwischen zwei Punkten auf der Erde messen will, muß man eigentlich noch die Erdkrümmung berücksichtigen. Bei geringen Entfernungen macht das keinen nennenswerten Unterschied.

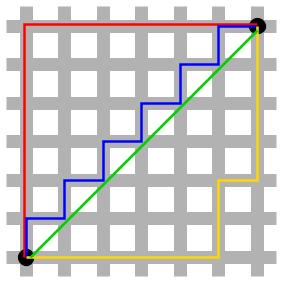
Wenn man sich aber in einer Stadt zwischen den beiden Punkten bewegen will, kann man nicht die Luftlinie nehmen, sondern muß sich entlang des Straßennetzes bewegen. Wenn zum Beispiel, wie in Manhattan oder Mannheim, die Straßen alle rechtwinklig zueinander sind, erhält man dann als Abstand die Summe der Differenzbeträge. Um diesen Abstand ging es in der Aufgabe aus dem PISA-Test ging, und der größer ist als der euklidische Abstand.

Ein anderes Beispiel ist die SNCF-Metrik. (SNCF ist die französische Eisenbahngesellschaft). Hier wird der Abstand zwischen zwei Punkten so berechnet, daß man zunächst den Abstand (in Luftlinie) des ersten Punktes nach Paris mißt, dann den Abstand von Paris zum zweiten Punkt, und die Summe bildet. 

Es gibt also verschiedene Möglichkeiten, Abstände zu messen. Alle diese Abstände haben mathematisch ähnliche Eigenschaften, weshalb man sie unter dem Begriff des Metrischen Raumes zusammenfaßt. Dies ist, per Definition, eine Punktmenge, auf der eine Abstandsfunktion definiert ist mit folgenden Eigenschaften:
1. je zwei unterschiedliche Punkte haben positiven Abstand (und der Abstand eines Punktes zu sich selbst ist 0)
2. der Abstand von x nach y ist genau so groß wie der Abstand von y nach x
3. die Dreiecksungleichung gilt (d.h. der Abstand von x nach y ist höchstens so groß, als wenn man erst den Abstand von x zu einem dritten Punkt z, dann den Abstand von z nach y mißt, und die Summe bildet)

Punkt 2. bedeutet natürlich wieder einmal eine Vereinfachung, weil man zum Beispiel Einbahnstraßen nicht in Betracht zieht.

Es ist eine beliebte Hausaufgabe für Analysis I-Vorlesungen, nachrechnen zu lassen, dass die Manhattan-Metrik und die SNCF-Metrik die 3 Axiome erfüllen. Der einzige schwierige Teil ist dabei das Nachrechnen der Dreiecksungleichung.

Eine sehr skurille (aber völlig ernstgemeinte) Anwendung metrischer Räume auf juristische Probleme des Drogenhandels in Manhattan wurde am 23. November 2005 in der New York Times vorgestellt.

Im Court of Appeals war der Fall von James R. verhandelt worden, der im März 2002 Drogen im Abstand von weniger als 1000 Feet von einer Schule verkauft hatte - was eine deutlich höhere Strafe impliziert als eine Entfernung von mehr als 1000 Feet. James R. war in Manhattan an der Kreuzung von Eighth Avenue und 40th Street beim Verkauf an einen Undercover-Polizisten verhaftet worden, die nächstgelegene Schule war Holy Cross an der 43rd Street zwischen Eighth und Ninth Avenue.
"Law enforcement officials calculated the straight-line distance using the Pythagorean theorem (a²+b²=c² ) measuring the distance up Eighth Avenue (764 feet) as one side of a right triangle, and the distance to the church along 43rd Street (490 feet) as another, to find that the length of the hypotenuse was – 907.63 feet."
Mißt man die Entfernung entlang der rechtwinklig verlaufenden Straßen wie in der PISA-Aufgabe, dann ist der Abstand natürlich 764+490=1254 Feet, und so argumentierte auch R.s Anwalt. Richter und Jury ließen sich davon freilich nicht beeindrucken und lehnten die Berufung einstimmig ab.
"Pythagoras won his day in court on Tuesday."
kommentierte Michael Cooper in der New York Times. Ein Richter in meinem (früheren) Schachverein meinte dazu, sonst könne man ja auch gleich Einbahnstraßen und Baustellen auf Bürgersteigen geltend machen.