
Mathematische Seitensprünge
Ein unbeschwerter Ausflug in das Wunderland zwischen Mathematik und Literatur
Alexander Mehlmann
Vieweg, 2007, 172 Seiten, 24,90 €
ISBN: 3-834-80175-5
Dachten Sie bei Goethes Faust bisher an Mathematik? Nein? Vielleicht bei Dantes Göttlicher Komödie oder Flauberts Madame Bovary? Auch nicht?
Nun, damit sind Sie wahrscheinlich nicht allein. Alexander Mehlmann stellt da wohl eher eine Ausnahme dar, doch ist er mit seinem Buch Mathematische Seitensprünge auf einem guten Weg, dies ein wenig zu ändern. Einen "unbeschwerten Ausflug in das Wunderland zwischen Mathematik und Literatur" verspricht er uns im Untertitel und erfüllt dieses Versprechen auch auf ganzer Linie.
Es geht dabei nicht nur darum, in klassischen Werken der Literatur mathematische Momente aufzuspüren, wie etwa der Vermessung der Höllenstreifen in Dantes bereits angesprochener Göttlichen Komödie, sondern es wird auch der Weg von der Mathematik zur Literatur eingeschlagen. So finden sich im 6. Kapitel eine Vielzahl mathematischer Gedichte des Autors, über deren lyrische Qualität an dieser Stelle nicht geurteilt werden soll, phantasievoll und faszinierend sind sie in jedem Fall.
Der Autor selbst, Alexander Mehlmann, ist Professor am Institut für Wirtschaftsmathematik der Technischen Universität in Wien, lehrt und forscht auf dem Gebiet der Spieltheorie und hat in diesem Zusammenhang bereits Goethes Faust und die Legende vom Wahnsinn des Odysseus als mathematische Spiele modelliert.
Das vorliegende Buch richtet sich an "ein Publikum, welches bereit ist, literarische Motive aus dem Blickwinkel der Mathematik zu betrachten und sich andererseits auch auf poetischem Weg der Faszination Mathematik zu nähern."
Um noch einmal auf Dante zurückzukommen, so ergibt sich durch Verhältnisrechnungen seiner Angaben übrigens eine Körpergröße Luzifers von 1,5 km.
Nicht alles in diesem Buch, wenn man ehrlich ist sogar eher wenig, ist absolut ernst zu nehmen, und zum Teil wird auch mit der auf Außenstehende (d.h. in diesem Fall Nichtmathematiker) häufig so kompliziert wirkenden Abstraktion und der Möglichkeit, einfache Alltagserkenntnisse in komplexe Formelsprache zu übersetzen, versucht ,Erstaunen oder Eindruck hervorzurufen.
So lässt sich beispielsweise der jeweilige Nutzen der Abmachung zwischen Mephisto und Faust in Abhänigigkeit der Zeit in tollen Formeln
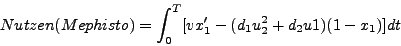
und
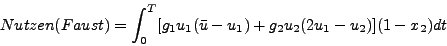
darstellen, wobei die einzelnen Variablen für Funktionen, wie die jeweilige Erwartung an den Zeitpunkt des Inkrafttreten des Pakts (x1 und x2) oder das momentane Reuempfinden von Faust (u2), stehen.
Andere tolle Formeln beschreiben die optimale Strategie des Blutsaugens für dynamische Vampire in nichtlinearen Differentialgleichungen, in welchen unter anderem die Wachstumsrate der Bevölkerung oder die Ausfallrate von Vampiren durch direkten Kontakt mit Sonnenstrahlen, Knoblauch oder ähnlich wirkenden Substanzen berücksichtigt werden müssen. Mehlmann kann aufgrund seiner Berechnungen sogar eine Typologie von Vampiren in "asymptotisch sättigbare", "blutmaximierende" und "unersättliche" Vampire erstellen.
Ein weiterer schöner Vorschlag ist, der Begriff der Hydronacci-Zahlen. Hierbei handelt es sich im Grunde zwar nur um die bereits bekannten Fibonacci-Zahlen, doch motiviert Mehlmann deren Definition über den Verlauf der Anzahl der Köpfe der Hydra, wenn diese Herakles mit einem (sozusagen einem Startkopf) gegenübertritt und dieser im Verlaufe seines Kampfes diese Köpfe unter Einhaltung einer gewissen, festgelegten Regel abschlägt.
Falls Sie immer noch nicht davon überzeugt sind, wie eng Mathematik und Literatur miteinander verbunden sind, so werden Sie während der Lektüre noch Petrarca, Odysseus, Puschkin und vielen anderen Literaten und literarischen Figuren begegnen.
Wie angekündigt, sind die Mathematischen Seitensprünge ein "faszinierender Spaziergang zwischen Mathematik und Literatur."
(Rezension: Joerg Beyer)



