Nach dem
Rätsel vorletzte Woche wurde in den Kommentaren angefragt, auch die anderen Teile des KIAS-Wandkalenders hier mal vorzustellen. Das werde ich in dann in Zukunft jeweils Anfang des Monats machen, heute zunächst noch als Nachtrag die Kalenderblätter von März und April 2014.
Der März:
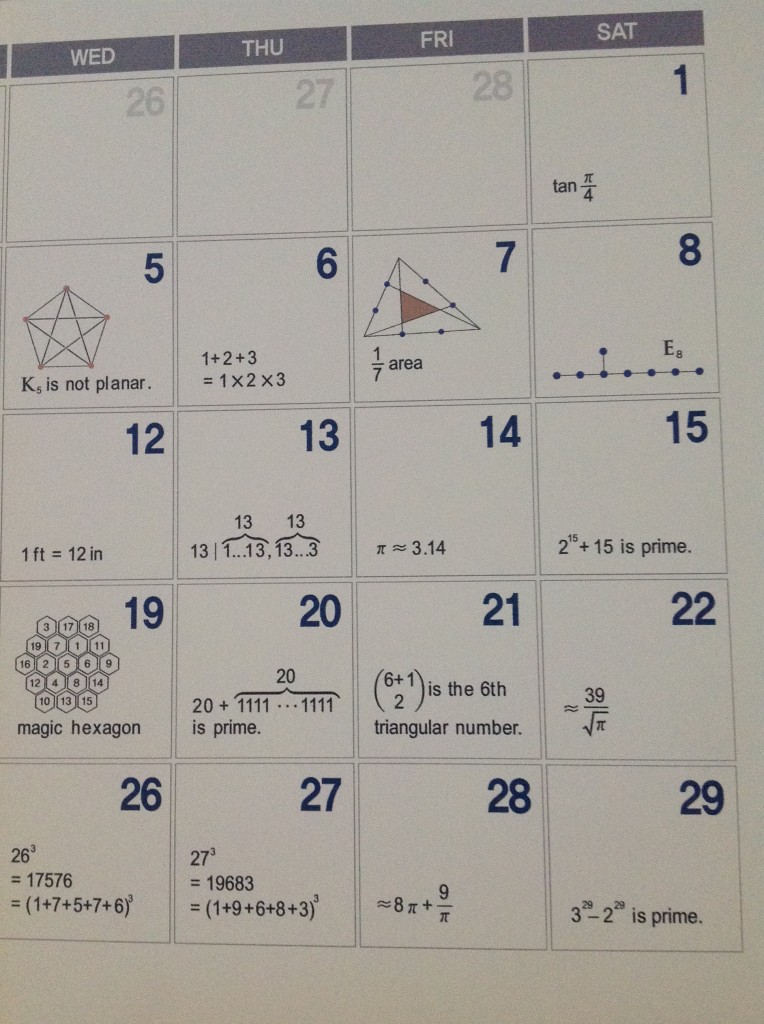
(Die abgeschnittenen Tage kommen unten noch mal.) Vieles ist wohl selbsterklärend, zum Beispiel die
4 ergibt sich aus \(tan(\frac{\pi}{4})=1\) und bei der
5 bedeutet \(K_5\) den vollständigen Graph mit 5 Ecken (also: jede Ecke ist mit jeder anderen verbunden) der sich nicht ohne Überkreuzungen in der Ebene zeichnen läßt - ein Spezialfall des
Satzes von Kuratowski.
Die
7 zeigt einen Spezialfall des
Satz von Routh, bei der
8 steht \(E_8\) für das
Dynkin-Diagramm \(E_8\), über dessen Anwendungen man einen eigenen Artikel schreiben könnte,
21 ist eine Dreieckszahl, weil man sie als Summe \(1+\ldots+6\) erhält, die bei
25 erwähnte Shapiro-Ungleichung besagt, dass für ungerade Zahlen \(n<25\) (oder für gerade Zahlen \(n<14\)) alle n-Tupel positive Zahlen die Ungleichung \(\sum_{i=1}^n\frac{x_i}{x_{i+1}=x_{i+2}}\ge\frac{n}{2}\) erfüllen.
Unklar ist mir noch, wie man die Prim-Eigenschaft von \(3^{29}-2^{29}\) beweist. Durch Nachrechnen wohl eher nicht.
Und der April:
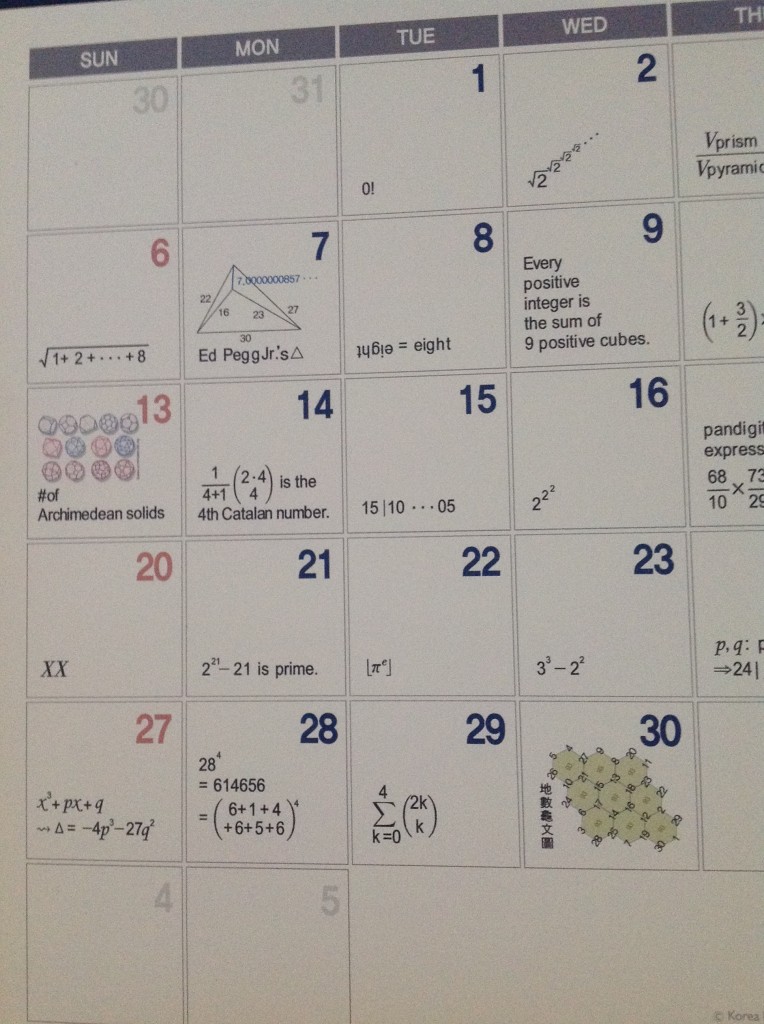
Die
9 beschreibt einen Spezialfall des
Waringschen Problems,
13 ist die Anzahl
archimedischer Körper (konvexe Körper mit regelmäßen Seitenflächen und transitiv auf den Ecken operierender Symmetriegruppe),
14 ist eine
Catalan-Zahl, nämlich die Anzahl der Triangulierungen eines Sechsecks,
19 ist die Anzahl der
partiellen Ordnungen auf einer drei-elementigen Menge, die Primzahleigenschaft bei der
21 habe ich ebenfalls nicht nachrechnen wollen,
27 zeigt einen Teil der
Lösungsformel für kubische Gleichungen (wobei die 4 und die 27 m.E. im Nenner stehen sollten) und bei der
30 haben alle Sechsecke die selbe Summe.
Nachtrag: Wegen einer Frage in den Kommentaren hier noch ein Gesamtbild:
(Die abgeschnittenen Tage kommen unten noch mal.) Vieles ist wohl selbsterklärend, zum Beispiel die 4 ergibt sich aus \(tan(\frac{\pi}{4})=1\) und bei der 5 bedeutet \(K_5\) den vollständigen Graph mit 5 Ecken (also: jede Ecke ist mit jeder anderen verbunden) der sich nicht ohne Überkreuzungen in der Ebene zeichnen läßt - ein Spezialfall des Satzes von Kuratowski.
Die 7 zeigt einen Spezialfall des Satz von Routh, bei der 8 steht \(E_8\) für das Dynkin-Diagramm \(E_8\), über dessen Anwendungen man einen eigenen Artikel schreiben könnte, 21 ist eine Dreieckszahl, weil man sie als Summe \(1+\ldots+6\) erhält, die bei 25 erwähnte Shapiro-Ungleichung besagt, dass für ungerade Zahlen \(n<25\) (oder für gerade Zahlen \(n<14\)) alle n-Tupel positive Zahlen die Ungleichung \(\sum_{i=1}^n\frac{x_i}{x_{i+1}=x_{i+2}}\ge\frac{n}{2}\) erfüllen.
Unklar ist mir noch, wie man die Prim-Eigenschaft von \(3^{29}-2^{29}\) beweist. Durch Nachrechnen wohl eher nicht.
Und der April:
Die 9 beschreibt einen Spezialfall des Waringschen Problems, 13 ist die Anzahl archimedischer Körper (konvexe Körper mit regelmäßen Seitenflächen und transitiv auf den Ecken operierender Symmetriegruppe), 14 ist eine Catalan-Zahl, nämlich die Anzahl der Triangulierungen eines Sechsecks, 19 ist die Anzahl der partiellen Ordnungen auf einer drei-elementigen Menge, die Primzahleigenschaft bei der 21 habe ich ebenfalls nicht nachrechnen wollen, 27 zeigt einen Teil der Lösungsformel für kubische Gleichungen (wobei die 4 und die 27 m.E. im Nenner stehen sollten) und bei der 30 haben alle Sechsecke die selbe Summe.
Nachtrag: Wegen einer Frage in den Kommentaren hier noch ein Gesamtbild:
