Im neuen SPIEGEL findet sich ein äußerst überschwänglich geschriebener Artikel zur (nicht ganz neuen) Datenbank LMFDB (L-functions and Modular Forms Database).
Was sind
L-Funktionen? Das einfachste Beispiel ist die
Riemannsche ζ-Funktion, die für Re(s)>1 durch \(\zeta(s) = \sum_{n=1}^\infty\frac1{n^s}=1+\frac1{2^s}+\frac1{3^s}+\frac1{4^s}+\frac1{5^s}+\frac1{6^s}+\frac1{7^s}+\ldots\) definiert und dann durch analytische Fortsetzung auf der restlichen komplexen Zahlenebene definiert wird. Riemann hatte sie in Zusammenhang mit der Berechnung der relativen Anzahl von Primzahlen betrachtet: wenn die Riemannsche Vermutung über die Nullstellen seiner Zeta-Funktion zutrifft, dann läßt sich die Fehlerabschätzung im
Primzahlsatz nicht weiter verbessern.
Allgemeiner kann man L-Funktionen beispielsweise für Darstellungen zyklischer Gruppen (
Dirichletsche L-Funktion), für Zahlkörper (
Dedekindsche L-Funktion), für elliptische Kurven, für Modulformen (Heckesche L-Funktion), für automorphe Formen (
automorphe L-Funktion), für Galois-Darstellungen (
Artinsche L-Funktion) etc.pp. definieren. Alle diese Funktionen haben ähnliche Eigenschaften, etwa bestimmte Funktionalgleichungen und die spezielle Lage von Null- und Polstellen.
Das
Langlands-Programm stellt Zusammenhänge zwischen unterschiedlich definierten L-Funktionen her und fast alles, was heutzutage in der Zahlentheorie gemacht und bewiesen wird, beruht in irgendeiner Form auf diesen L-Funktionen. Trotzdem ist das Gerede von einer 'Weltformel der Mathematik' (im neuen SPIEGEL und auch anderswo) natürlich ziemlich übertrieben; zum Verständnis bspw. von Differentialgleichungen tragen L-Funktionen eher wenig bei.
Die neue Datenbank liefert nun Millionen Datensätze mit denen man die aus unterschiedlichen Gebieten stammenden L-Funktionen untersuchen und vergleichen kann. Ein paar Musterbeispiele:
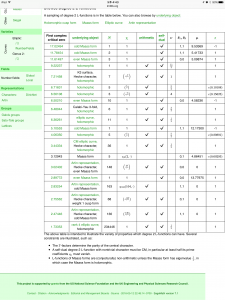
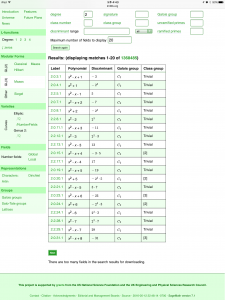
Link zur Datenbank
Was sind L-Funktionen? Das einfachste Beispiel ist die Riemannsche ζ-Funktion, die für Re(s)>1 durch \(\zeta(s) = \sum_{n=1}^\infty\frac1{n^s}=1+\frac1{2^s}+\frac1{3^s}+\frac1{4^s}+\frac1{5^s}+\frac1{6^s}+\frac1{7^s}+\ldots\) definiert und dann durch analytische Fortsetzung auf der restlichen komplexen Zahlenebene definiert wird. Riemann hatte sie in Zusammenhang mit der Berechnung der relativen Anzahl von Primzahlen betrachtet: wenn die Riemannsche Vermutung über die Nullstellen seiner Zeta-Funktion zutrifft, dann läßt sich die Fehlerabschätzung im Primzahlsatz nicht weiter verbessern.
Allgemeiner kann man L-Funktionen beispielsweise für Darstellungen zyklischer Gruppen (Dirichletsche L-Funktion), für Zahlkörper (Dedekindsche L-Funktion), für elliptische Kurven, für Modulformen (Heckesche L-Funktion), für automorphe Formen (automorphe L-Funktion), für Galois-Darstellungen (Artinsche L-Funktion) etc.pp. definieren. Alle diese Funktionen haben ähnliche Eigenschaften, etwa bestimmte Funktionalgleichungen und die spezielle Lage von Null- und Polstellen.
Das Langlands-Programm stellt Zusammenhänge zwischen unterschiedlich definierten L-Funktionen her und fast alles, was heutzutage in der Zahlentheorie gemacht und bewiesen wird, beruht in irgendeiner Form auf diesen L-Funktionen. Trotzdem ist das Gerede von einer 'Weltformel der Mathematik' (im neuen SPIEGEL und auch anderswo) natürlich ziemlich übertrieben; zum Verständnis bspw. von Differentialgleichungen tragen L-Funktionen eher wenig bei.
Die neue Datenbank liefert nun Millionen Datensätze mit denen man die aus unterschiedlichen Gebieten stammenden L-Funktionen untersuchen und vergleichen kann. Ein paar Musterbeispiele:
Link zur Datenbank