„Hier kann Mathematik helfen, die Demokratie selbst zu stärken“
Fair sind demokratische Wahlen nur bei gleich großen Wahlkreisen. Wandern Wähler zu oder ab, müssen die Kreise angepasst werden – eine komplexe und politisch kontroverse Aufgabe. Ein neues mathematisches Verfahren findet schnell ausgewogene Wahlkreise.
Wer wählt geht davon aus, dass seine Stimme genauso viel Einfluss hat wie jede andere. Deshalb sollten die Wahlkreise, gemessen an der Zahl der Wahlberechtigten, möglichst gleich groß sein. Sonst stünde es schlecht um die Akzeptanz der Wahl. Die Folge: Ändern sich Einwohnerzahlen, müssen Wahlkreise angepasst werden. Die Entscheidung, wie das zu tun ist, überlässt man besser nicht politischen Parteien.
Die Mathematik kann helfen: Forscher um Peter Gritzmann von der Technischen Universtität München, entwickelten eine neue Methode, mit der sich der optimale Zuschnitt von Wahlkreisen politisch neutral berechnen lässt. Diese sei effizienter als bisherige Methoden. Dafür verwendeten sie ein in der Arbeitsgruppe entwickeltes mathematisches Modell: Das „Geometric Clustering“ gruppiert die Gemeinden zu Clustern, den optimierten Wahlkreisen. Rechnerisch ist das ein beträchtlicher Aufwand. „Es gibt mehr Möglichkeiten, die Gemeinden in Deutschland zu Wahlkreisen zusammenzufassen, als Atome im bekannten Universum“, sagt Gritzmann.
Getestet haben die Mathematiker ihr Verfahren am Beispiel der derzeit 299 Wahlkreise für den deutschen Bundestag. Laut Bundeswahlgesetz soll deren Bevölkerungszahl nicht mehr als 15 Prozent von der Durchschnittsgröße abweichen, bei mehr als 25 Prozent muss ein Wahlkreis zwingend neu festgelegt werden. Außerdem muss die Berechnung zusammenhängende Gebiete ergeben und die Grenzen der Bundesländer, Landkreise und Kommunen sollen eingehalten werden. „Mit unserem Modell können wir dennoch effizient Lösungen finden, bei denen alle Kreise annähernd die gleiche Zahl von Stimmberechtigten aufweisen – und das sogar, ‚minimalinvasiv’, ohne dass auch nur ein einziger Wahlberechtigter seinen Stimmbezirk wechseln muss“, findet Gritzmann.
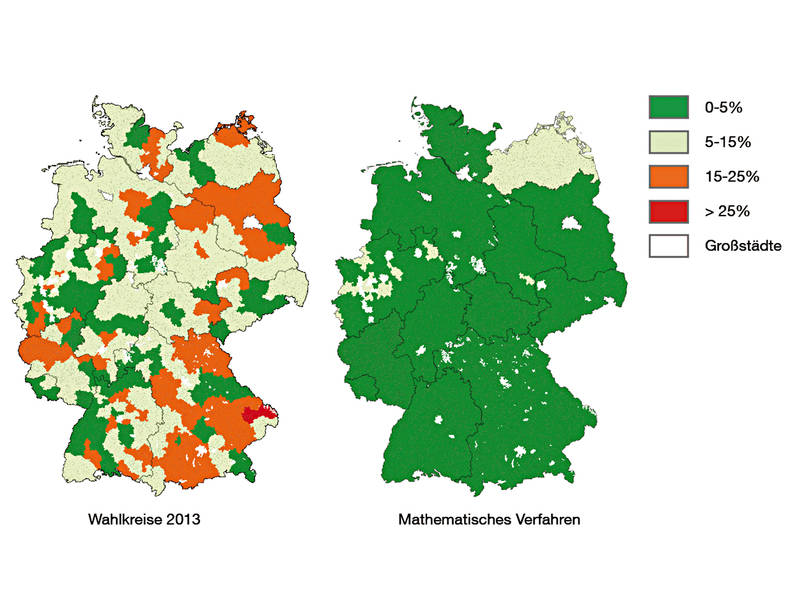 In einzelnen der 2012 für die kommende Wahl neu zugeschnittenen Wahlkreise ergaben sich durch Zu- und Wegzug schon im Wahljahr 2013 Abweichungen (links), die über dem angestrebten Maximalwert liegen. Mit der mathematischen Methode werden deutlich geringere Abweichungen erzielt. Sie bietet damit eine größere Toleranz gegenüber Bevölkerungsveränderungen in der Zeit bis zur Wahl. (Bild: F. Klemm/ TUM)
In einzelnen der 2012 für die kommende Wahl neu zugeschnittenen Wahlkreise ergaben sich durch Zu- und Wegzug schon im Wahljahr 2013 Abweichungen (links), die über dem angestrebten Maximalwert liegen. Mit der mathematischen Methode werden deutlich geringere Abweichungen erzielt. Sie bietet damit eine größere Toleranz gegenüber Bevölkerungsveränderungen in der Zeit bis zur Wahl. (Bild: F. Klemm/ TUM)
Die Methode lasse sich auch auf andere Staaten anwenden. Weiterhin könnten damit und im adäquater Tarifgruppen für Versicherungen bestimmt oder hybride Materialien modelliert werden. „Die Wahlkreiseinteilung ist jedoch eine ganz besondere Anwendung, denn hier kann Mathematik helfen, die Demokratie selbst zu stärken“, resümiert Gritzmann.
Karte der optimierten Wahlkreise: www-m9.ma.tum.de/material/districting/
Quelle: www.tum.de/die-tum/aktuelles/pressemitte...etail/article/33968/
Paper: www.sciencedirect.com/science/article/pii/S037722171730351X
Links zum Thema Gerrymandering mit Beispielen aus den Deutschland und den USA
- Modellansatz Podcast mit Prof. Marco Lübbecke www.math.kit.edu/ianm4/seite/ma-operations-research/de
- www.nature.com/news/the-mathematicians-w...ureNews&sf86024060=1
- www.quantamagazine.org/the-mathematics-b...rymandering-20170404



