Die Geometrie gab es schon vor der Erschaffung der Welt. Johannnes Kepler
Räumliche Distanzierung
Drei Semester lang sollte man einen Mindestabstand von d=1,5 Metern einhalten. Wie sollten sich Studenten unter dieser Vorgabe optimal aufstellen? Diese naheliegende Frage griff Andrés Navas im Juni 2020 auf Images des Mathématiques auf. Wenig überraschend ist für eine Gruppe von 4 Personen das Quadrat optimal. Das aus zwei gleichseitigen Dreiecken gebildete Parallelogramm hätte zwei Ecken mit größerem Abstand als die gegenüberliegenden Ecken im Quadrat: der Maximalabstand zwischen zwei Personen ist im Quadrat \(\sqrt{2}d\), im 60-Grad-Parallelogramm \(\sqrt{3}d\). Tatsächlich kann man beweisen: wenn sich vier Personen mit paarweisem Mindestabstand d aufstellen, dann gibt es mindestens ein Paar mit Abstand mindestens \(\sqrt{2}d\). Im dreidimensionalen Raum kann man vier Personen sogar so anordnen, dass alle jeweils den Abstand d voneinander haben: man setzt sie auf die Ecken eines regelmäßigen Tetraeders. Das ist freilich unpraktikabel; obwohl wir von räumlicher Distanzierung sprechen, meinen wir doch die Aufstellung in einer Ebene. Wie sieht es aus, wenn man mehr als 4 Personen anordnen will? Dann ist die optimale Anordnung in der Ebene nicht die Aufstellung auf den Ecken eines Quadratgitters. Stattdessen ist es effektiver, die Menschen auf den Ecken eines aus regelmäigen Dreiecken bestehenden Gitters aufzustellen, wie Navas in einem weiteren Artikel im August 2020 diskutierte. Äquivalent kann man die Menschen auch auf die Mittelpunkte eines Sechseckgitters stellen, man erhält so dieselbe Anordnung.
In Chile, wo ja im Juni Winter ist, wütete Corona (wie in ganz Südamerika und Südafrika) im Sommer 2020 besonders stark. Navas, der in Santiago de Chile arbeitet, erwähnte in seinem Artikel, dass man in diesen Tagen an manchen Orten auf den Boden gemalte Sechsecke zur räumlichen Distanzierung sah, wie auf diesem Foto aus seiner Heimatstadt:
Wenn Menschen sich in die Mittelpunkte dieser Sechsecke stellen, erreichen sie die geforderte räumliche Distanzierung bei minimalem Flächenverbrauch. Auch manche Pariser U-Bahnhöfe (z.B. der Gare du Nord) zeichneten auf einem Dreiecksgitter liegende Kreise auf den Boden, andere (z.B. der Gare de Saint-Denis) ordneten die Kreise auf einem Quadratgitter an.
Minkowski-Summen
Abstandsregeln gab es auch schon vor Corona. In Bayern fanden im März 2020 Kommunalwahlen statt. Für den Wahlkampf hatte sich die AfD in Augsburg am 29. Februar den strategisch günstigsten Platz am Königsplatz gesichert: wegen des Bundesligaspiels kommen dort am Samstagnachmittag Tausende Fußballfans vorbei, um mit der Tram zur WWK-Arena zu fahren. (Im Nachhinein war das für lange Zeit das letzte Wochenende, an dem man solche Veranstaltungen durchführen konnte, aber das war damals natürlich noch nicht abzusehen.) Anscheinend gibt es eine Regel, dass Gegendemonstranten einen Mindestabstand zum Wahlkampfstand einhalten müssen. Deshalb wurde der Stand mit einer Kreidezeichnung eingekreist, samt der mit Kreide geschriebenen Aufforderung, die Einkreisung zu umgehen.
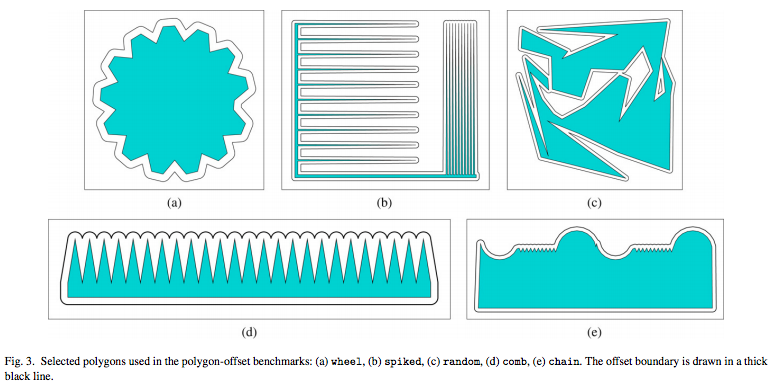
Das wirft natürlich eine geometrische Frage auf: was ist die minimale Umgebung, die zu einem gegebenen Rechteck überall den vorgegebenen Abstand einhält? Man denkt spontan an eine Ellipse und die Fotos legen das vielleicht auch nahe. In Wirklichkeit ist es aber einfacher. Zu einer gegebenen Menge R (dem Rechteck) und einer positiven Zahl d (dem Mindestabstand) ist die gesuchte Menge \(\left\{x \colon min(d(x,r):r\in R)\le d\right\}\) (per Definition) die "Minkowski-Summe" aus R und dem Kreis vom Radius d. Diese Menge wird auch als „offset polygon“ (deutsch vermutlich „Versatz-Polygon“) bezeichnet. Dieses ist stets ein größeres Polygon mit abgerundeten Ecken, im Falle des Rechtecks also einfach ein größeres Rechteck, bei dem man die Ecken abgerundet hat. Das nächste Bild aus einer Arbeit von Ron Wein zeigt die Offset-Polygone einiger komplizierterer Mengen.
Verschiedene Dimensionen
Räumliche Distanzierung ist ja in Wirklichkeit Distanzierung in der Ebene. Die Optimalität des hexagonalen Gitters für Kreispackungen der Ebene bewies 1940 László Fejes Tóth, die optimale Dichte ist \(\frac{\pi}{\sqrt{12}}\). Das sehr viel schwerere dreidimensionale Problem ist als Kepler-Vermutung bekannt. Deren Geschichte begann Ende des 16. Jahrhunderts, als der englische Seefahrer Walter Raleigh seinen mathematischen Assistenten Thomas Harriot nach einer Formel für die Anzahl der Kanonenkugeln in einem gegeben Stapel fragte. Harriot lieferte diese Formel und fragte sich dann, wie man die Anzahl der Kanonenkugeln im Laderaum eines Schiffes maximiert. Dieses Problem formulierte er in einem Brief an Johannes Kepler, der daraufhin 1611 die Broschüre “Vom sechseckigen Schnee” veröffentlichte mit der vermuteten optimalen Anordnung von Kugeln, deren Dichte \(\frac{\pi}{\sqrt{18}}\) ist. Das und sehr viel mehr zur Geschichte kann man nachlesen in George Szpiros 2011 in deutscher Übersetzung erschienenem Buch Die Keplersche Vermutung.
Die dreidimensionale Kepler-Vermutung wurde bekanntlich von Thomas Hales gelöst. "Was Früchteverkäufer seit Jahrhunderten wissen, hat endlich auch die Mathematik bewiesen: Platzsparender als bei den kunstvoll aufgetürmten Orangen-Pyramiden auf dem Wochenmarkt kann man Kugeln nicht aufeinanderschichten." schrieb die ZEIT im März 1999. Hales' Beweis benutzte umfangreiche Computerrechnungen und die Gutachter meinten seinerzeit, sie seien (nur?) zu 99 Prozent von der Richtigkeit des Beweises überzeugt. Hales startete deshalb 2003 ein Projekt, einen formalen computerlesbaren Beweis zu erstellen, der von HOL überprüft werden kann. Dieses Projekt wurde 2014 zu einem erfolgreichen Abschluß gebracht. Das Resultat war der Satz |- import tame classification \(\wedge\) the nonlinear inequalities \(\Longrightarrow\) the kepler conjecture, wobei the kepler conjecture definiert ist durch
Die Erklärung dazu findet man auf der Webseite des Flyspeck Project (meine Übersetzung): Für jede Packung V (gegeben durch die Mittelpunkte der Kugeln vom Radius 1) gibt es eine den Fehlerterm kontrollierende Konstante c, so dass für jedes \(r\ge 1\) die Anzahl der Kugelmittelpunkte innerhalb eines kugelförmigen Behälters vom Radius r höchstens \(\pi r^3/\sqrt{18}\) plus ein Fehlerterm kleinerer Ordnung ist. Für r gegen unendlich gibt das die Dichte \(\pi / \sqrt{18}= 0.74\ldots\), was die Dichte der flächenzehtrierten kubischen Packung ist. In höheren Dimensionen war lange nichts bekannt. Eine Arbeit von Maryna Viazovska lieferte schließlich im März 2016 die optimale Dichte \(\frac{\pi^4}{384}\) in Dimension 8. Bemerkenswerterweise hatte diese Lösung der 8-dimensionalen Version der Kepler-Vermutung einen viel kürzeren Beweis als das 3-dimensionale Problem. Viazovskas Arbeit "The sphere packing problem in dimension 8" bewies die Optimalität der durch das E8-Gitter gegebenen 8-dimensionalen Kugelpackung auf nur 22 Seiten (von denen ein Teil expositorisch ist, z.B. erhielt der Leser nebenbei noch eine Einführung in die Theorie der Modulformen). Der Beweis baute noch auf einer älteren Arbeit von Cohn und Elkies auf, die aber auch nur 25 Seiten lang war. Neben der Kürze überraschte am Beweis vor allem die Methodik: wichtigstes Werkzeug im Beweis sind Modulformen, sonst eigentlich ein unverzichtbares Werkzeug der Zahlentheorie. Das Schlagwort E8 wird vielen aus der Physik bekannt sein, nicht zuletzt durch die Ende der Nuller Jahre diskutierte Exceptionally Simple Theory of Everything, die die größte exzeptionelle Lie-Gruppe E8 benutzte. Die Lie-Algebra dieser Lie-Gruppe wird durch ein Wurzelsystem aus 240 Wurzeln im R8 beschrieben, welches (nach Projektion in den dreidimensionalen Raum) so aussieht:
Dieses Gitter im 8-dimensionalen Raum wird durch eine einfache Formel beschrieben:
\(\left\{(x_1,\ldots,x_8)\in Z^8\cup(Z+\frac{1}{2})^8: x_1+\ldots+x_8 = 0\ mod\ 2\right\}\).
Die 8-dimensionalen Kugeln vom Radius 1 um diese Gitterpunkte liefern eine Kugelpackung der Dichte \(\frac{\pi^4}{384}\). Cohn und Elkies hatten in einer 2003 veröffentlichten Arbeit gezeigt, dass man mittels der Fourier-Transformation \(\widehat{f}(y)=\int_{{\bf R}^n}f(x)e^{-2\pi ix.y}dx\) sogenannter “zulässiger Funktionen” \(f\colon{\bf R}^n\to{\bf R}\) obere Schranken für die Dichte von Kugelpackungen beweisen kann. Die "zulässigen Funktionen" sind Funktionen, für die
\(\vert f(x)\vert \le C(1+\vert x\vert)^{-n-\delta}, \vert\widehat{f}(y)\vert\le C(1+\vert y\vert)^{-n-\delta}\)
mit geeigneten Konstanten C und δ gilt. Für eine beliebige solche Funktion mit \(f(x)\le 0\) für \(\vert x\vert \ge 1\) und \(\widehat{f}(y)\ge 0\) für alle y bewiesen Cohn und Elkies, dass \(\frac{f(0)}{\widehat{f}(0)}\frac{\pi^\frac{n}{2}}{2^n\Gamma(\frac{n}{2}+1)}\) eine obere Schranke für die Dichte jeder n-dimensionalen Kugelpackung liefert. Für n=8 gibt das die obere Schranke \(\frac{f(0)}{\widehat{f}(0)}\frac{1}{16}\frac{\pi^4}{384}\) und um die Optimalit\"at des E8-Gitters zu beweisen musste dann also "nur" noch eine den Ungleichungen genügende zulässige Funktion mit \(\frac{f(0)}{\widehat{f}(0)}=16\) gefunden werden. Viazovskas Konstruktion einer solchen Funktion f benutzte verschiedene Modulformen, nämlich die j-Funktion und die Theta-Funktionen. Der Ausdruck für die gesuchte Funktion war dann ziemlich kompliziert, er besteht aus 8 Summanden, die jeweils Integrale von verschiedenen Kombinationen dieser Funktionen sind, der fünfte Summand sah beispielsweise so aus:
\(\int_{-1}^i 128(\frac{\theta_{00}(z)^4+\theta_{01}(z)^4}{\theta_{10}(z)^8}+ \frac{\theta_{00}(z)^4+\theta_{10}(z)^4}{\theta_{01}(z)^8})e^{\pi i\parallel x\parallel^2z}dz\),
die anderen Summanden waren ähnlich kompliziert. Mittels der Symmetrieeigenschaften und der Abschätzungen für Fourierkoeffizienten von Modulformen wurde in ihrer Arbeit letztlich bewiesen, dass die konstruierte Funktion f die gewünschten Eigenschaften hat und es also nach Cohn-Elkies keine dichteren Kugelpackungen als das E8-Gitter geben kann. Wenige Wochen nach der Lösung des achtdimensionalen Problems bewies Viazovska dann mit Cohn, Kumar, Miller, Radchenko und mit ähnlichen Methoden in einer 17 Seiten langen Arbeit, dass das Leech-Gitter die optimale Kugelpackung im R24 liefert. Viele Mathematiker glauben, dass es in anderen Dimensionen als 8 und 24 keine so eleganten Lösungen geben wird.
Gauß-Vorlesung
Das Leech-Gitter ist ein Gitter im 24-dimensionalen Raum, das man mit Hilfe des in der Informationsübertragung wichtigen Golay-Codes konstruiert und mit dem in den 70er Jahren das Problem gelöst wurde, die maximale Zahl von einander berührenden Einheitssphären (Kusszahl) im 24-dimensionalen Raum zu finden. Es war im Juli 2021 das Thema der Gauß-Vorlesung (der halbjährlichen Veranstaltung der Deutschen Mathematiker-Vereinigung, mit der einer interessierten Öffentlichkeit ein Eindruck von aktueller Mathematik vermittelt werden soll), die an der Universität Augsburg coronabedingt online stattfand. Nach einigen kurzen Ansprachen und einem Eröffnungsvortrag von Jürgen Richter-Gebert über Spaziergänge in der vierten Dimension und speziell den 120-Zell (ein 4-dimensionales Polytop, dessen Rand aus 120 Dodekaedern besteht und als diskretisierte Hopf-Faserung verstanden werden kann) ging es im Hauptvortrag von Maryna Viazovska um das Leech-Gitter, seine Anwendungen auf Kugelpackungen und andere Optimierungsprobleme, und die Beziehungen zu Kodierungstheorie und Gruppentheorie. Trotz der relativ kurzfristigen Ankündigung nahmen mehrere hundert Zuschauer an der Online-Übertragung teil. Natürlich war es ein anderes Format als sonst von Gauß-Vorlesungen gewohnt, aber ein sehr interessanter Vortrag und auch das Programm vor- und nachher und die Diskussion sehr gut gemacht.
Das Video der Gauß-Vorlesung findet man auf https://youtu.be/eOtEgJFpP7w. Ebenfalls auf YouTube findet man einen ähnlichen, aber mehr ins mathematische Detail gehenden Vortrag, den Viazovska auf dem Azat-Miftakhov-Tag gehalten hat. Azat Miftakhov ist ein begabter Nachwuchsmathematiker und linker Aktivist, der von einem Moskauer Gericht wegen konstruierter Vorwürfe zu sechs Jahren Strafarbeit verurteilt wurde. Als Zeichen der Solidarität organisierte ein Unterstützerkomitee am 16. Juni eine online ausgetragene Veranstaltung, für die die aktuell bekanntesten unter den jungen osteuropäischen Mathematikern gewonnen werden konnten. Die Vorträge von Alexander Bufetov, Peter Scholze und Maryna Viazovska findet man auf dem YouTube-Kanal Day Azat Miftakhov.