Kaum eine Periode der Wissenschafts- und Technologiegeschichte war von einem derart radikalen Wandel und Fortschrittsdenken geprägt wie der Übergang vom 19. zum 20. Jahrhundert: Durch Elektrifizierung, Fortschritte im Transport- und Telekommunikationswesen oder die Etablierung der chemischen Industrie als eigenem Industriezweig verstand sich die Menschheit mehr denn je als eine Spezies, die in der Lage ist, ihre Umwelt aktiv zu gestalten und sie schlussendlich zu beherrschen. Der Welthandel florierte, die Absätze in der Industrie, aber auch die Erträge in der Landwirtschaft, die von der Industrialisierung nicht ausgeschlossen war, erhöhten sich um ein Vielfaches und Weltbevölkerung wuchs schneller als je zuvor. Mit London, Paris, Berlin, Wien und New York entstanden Mega-Cities, die in schier unaufhaltsamen Tempo weit über ihre ursprünglichen Stadtgrenzen hinauswuchsen und zu bedeutenden Zentren von Wirtschaft, Kultur und Wissenschaft avancierten.
Führende Industrienationen wie Frankreich, die USA, Deutschland und das Vereinigte Königreich wetteiferten um die ersten Plätze dieser Entwicklung. Die Bühnen dieses Wettstreits waren in jener Zeit die Weltausstellungen, auf denen Austeller aus aller Welt die neuesten technologischen Errungenschaften der breiten Öffentlichkeit vorstellten. Eine der bedeutendsten Weltausstellung war jene im Sommer 1900 in Paris, von deren Pracht heute noch das wohl bekannteste Wahrzeichen der Stadt, der Eiffelturm, zeugt. In diese Zeit fällt auch der zweite Internationale Mathematikerkongress in Paris, auf dem der große Mathematiker und damalige Präsident der Deutschen Mathematiker-Vereinigung, David Hilbert, am 8. August in der Sorbonne eine Rede hielt, die in ihrer Programmatik und ihrem Einfluss auf die Mathematik des 20. Jahrhunderts beispiellos sein sollte: Die Vorstellung der 23 Probleme.
Bei dieser vielzitierten Rede handelte es sich um einen Katalog von 23 Fragestellungen, mit dem Hilbert versuchte nicht nur dem Zeitgeist entsprechend, die Errungenschaften der damaligen Mathematik darzustellen (wie Poincare es drei Jahre zuvor auf dem ersten Internationalen Mathematiker-Kongress in Zürich getan hatte), sondern vor allem einen Blick nach vorne in die zukünftige Entwicklung der Mathematik zu wagen.
Wie viele andere Wissenschaften auch stand die Mathematik zur Jahrhundertwende am Anfang einer nie dagewesenen Entwicklung, die sich durch nahezu alle ihre Teilbereiche ziehen sollte. Den Grundstein dieser Entwicklung legte vor allem der von Hilbert sehr bewunderte Cantor, der mit seiner Mengenlehre die Mathematik erstmals auf ein strenges, formalistisch-logisches Fundament zu heben versuchte. Es ist daher wenig verwunderlich, dass Hilbert die Kontinuumshypothese, das zu dieser Zeit wichtigste Problem der Mengenlehre, gleich als erstes Problem auf seiner Liste nannte. Aber auch andere moderne Entwicklungen, die zu seiner Zeit noch in den Kinderschuhen steckten, wie die Diskrete Geometrie, zeugten von Hilberts Weitsicht.
Zahlreiche Entwicklungen in verschiedenen Bereichen der modernen Mathematik wurden mittelbar und unmittelbar von Hilberts Liste beeinflusst: Das Reziprozitätsgesetz von Artin etwa, aus dem sich später das Langlandsprogramm, ein bedeutendes Forschungsprogramm in der modernen Zahlentheorie entwickelte, lässt sich als Antwort auf das neunte Problem von Hilberts Liste auffassen.
Des Weiteren steht die Liste der Hilbertschen Probleme auch für eine zunehmende Internationalisierung der Mathematik: Waren zuvor vor allem Deutschland, Frankreich und Russland die führenden Mathematikernationen, arbeiteten an den Hilbertschen Problemen auch Mathematiker*innen aus Ländern, die zuvor keine oder nur wenige Beiträge zur europäisch dominierten mathematischen Forschung leisteten, etwa Japan, China und die USA.
Freilich konnte Hilbert nicht jede Entwicklung in der Mathematik im 20. Jahrhundert vorausahnen: Probleme aus den Gebieten der Graphen-, der Chaos- oder der Komplexitätstheorie, die in ihren Frühformen zu Hilberts Zeiten zwar bereits existierten, aber erst durch den Einsatz von Computern wirklich zu dem wurden, was sie heute sind, fanden in Hilberst Liste keine Beachtung; ebenso wenig die Topologie, die sich erst ca. zehn Jahre nach Hilberts Rede durch Hausdorff und Poincare als eine Hauptdisziplin etablierte. (Einzig das fünfte Problem lässt sich, wenn auch mit etwas Wohlwollen, der Topologie zuordnen). Fragestellungen aus der angewandten Mathematik, mit denen sich Hilbert erst später, beispielsweise mit Arbeiten zur Relativitätstheorie, beschäftigte, sind in der Liste unterrepräsentiert und die Stochastik, die dank der Arbeiten von Laplace, Bernoulli, Bayes, und Tschebycheff durchaus eine florierende Disziplin war (wenngleich erst 33 Jahre später durch Kolmogoroff axiomatisiert) tauchten gar nicht auf. Überraschenderweise fand auch die Fermatsche Vermutung, die seit ihrer Formulierung im 17. Jahrhundert eines der prominentesten offenen Probleme der Mathematik war (und erst in den 1990er Jahren durch Andrew Wiles gelöst wurde), nicht den Weg auf Hilberts Liste.
Eine weitere Entwicklung, die Hilbert nicht vorausahnen konnte, betraf das Wesen mathematischer Erkenntnis an sich: Seine zum geflügelten Wort gewordene Losung, in der Mathematik gebe es kein Ignorabimus (lat.: „wir werden nicht wissen“) [„Diese Überzeugung von der Löslichkeit eines jeden mathematischen Problems ist uns ein kräftiger Ansporn während der Arbeit; wir hören in uns den steten Zuruf: Da ist das Problem, suche die Lösung. Du kannst sie durch reines Denken finden; denn in der Mathematik gibt es kein Ignorabimus!“], mit der Hilbert seiner Überzeugung Ausdruck verleihen wollte, dass jedes in der Mathematik sinnvoll gestellte Problem prinzipiell auch lösbar sei, stellte sich wegen der Arbeiten Gödels zum Unvollständigkeitssatz und Turings zur Unlösbarkeit des Entscheidungsproblems als nicht mehr haltbar heraus.
Gleichwohl war die Liste der 23 Probleme so wegweisend und umfassend, dass die Mathematik heute ohne sie möglicherweise eine andere wäre. Sie ist zweifellos eines der einflussreichsten Stücke der Mathematikgeschichte und bildete, vielleicht neben dem Langlandsprogramm und der Klassifikation der endlichen einfachen Gruppen, eines der umfangreichsten Forschungsprogramme der neuzeitlichen Mathematik.
Ein von Hilbert nicht veröffentlichtes, aber für die ursprüngliche Liste vorgesehenes 24. Problem wurde im Jahr 2000 von dem Mathematikhistoriker Rüdiger Thiele von der Universität Leipzig in Hilberts Nachlass entdeckt. Es beschäftigt sich mit Beweistheorie, einem Teilgebiet der mathematischen Logik, bei der mathematische Sätze und vor allem ihre Beweise selbst Gegenstand der Forschung sind, siehe unten.
Zum 130. Jubiläum des Gründungstages der Deutschen Mathematiker-Vereinigung, herbeigeführt von Georg Cantor und David Hilbert, haben wir es uns zur Aufgabe gemacht, die Hilbertschen Probleme aufzuarbeiten und darzustellen. Wir haben dabei den Spagat versucht, einen Mittelweg zwischen allgemeiner Verständlichkeit und fachlicher Korrektheit zu finden. Wir wünschen viel Vergnügen bei der Lektüre.
Konrad Krug, DMV-Medienbüro
Problem 1: Gibt es eine Menge, die in ihrer Mächtigkeit größer als die natürlichen Zahlen, aber kleiner als die reellen Zahlen ist? ( Stichwort „Kontinuumshypothese“)
Antwort: Weder die Existenz noch die Nichtexistenz einer solchen Menge steht im Widerspruch zu den Standardaxiomen der Mengenlehre.
Die Mächtigkeit einer Menge ist eine Art Ausweitung des Begriffes der Anzahl der Elemente einer Menge auf unendliche Mengen. Zwei Mengen heißen dabei gleichmächtig, wenn man eine Eins-zu-Eins-Beziehung zwischen ihnen herstellen kann (endliche Mengen haben in diesem Falle gleichviele Elemente): Nach Cantors Diagonalargumenten haben die rationalen Zahlen beispielsweise zwar die gleiche Mächtigkeit wie die natürlichen Zahlen, aber eine kleinere als die reellen Zahlen.
 Die natürlichen, die rationalen und die reellen Zalen sind jeweils Teilmengen voneinander. Doch nur, weil eine Menge Teilmenge einer anderen ist, heißt das nicht, dass diese Mengen nicht in einer Eins-zu-Eins-Beziehung stehen können,…
Die natürlichen, die rationalen und die reellen Zalen sind jeweils Teilmengen voneinander. Doch nur, weil eine Menge Teilmenge einer anderen ist, heißt das nicht, dass diese Mengen nicht in einer Eins-zu-Eins-Beziehung stehen können,…
1938 konnte Gödel zeigen, dass die Annahme der Existenz einer solchen Menge nicht im Widerspruch zum ZFC genannten Axiomensystem der Mengenlehre steht – allerdings zeigte Cohen 1963 mit der sogenannten Forcing-Methode, dass auch die Annahme der Nichtexistenz einer derartigen Menge nicht zu Widersprüchen führt, eine Leistung, die später mit der Fields-Medaille gewürdigt wurde.
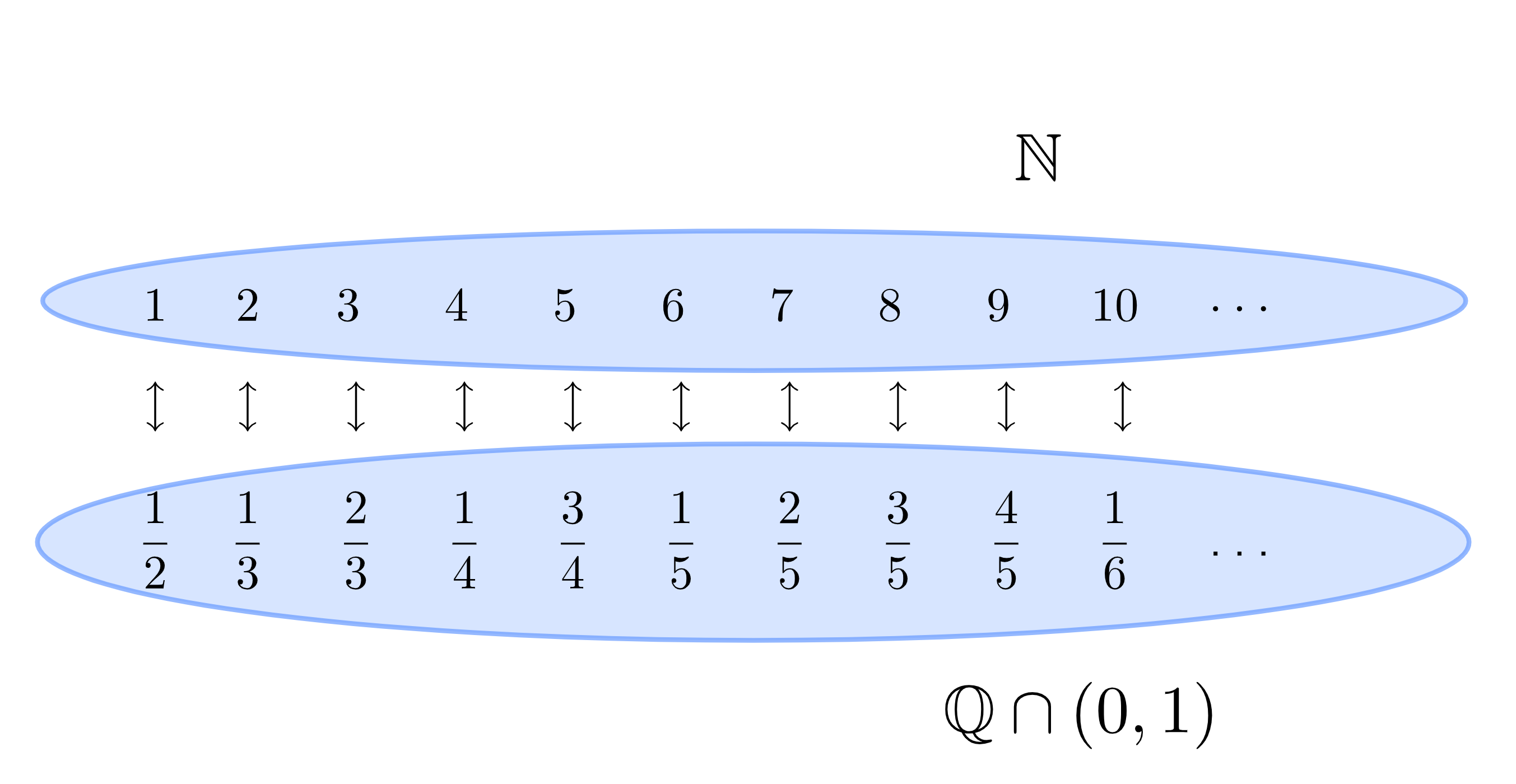 ,… wie Cantors erstes Diagonalargument zeigt: Die rationalen Zahlen (zwischen 0 und 1, das ist aber keine wesentliche Einschränkung der Aussage) und die natürlichen Zahlen stehen in einer Eins-zu-Eins-Beziehung.
,… wie Cantors erstes Diagonalargument zeigt: Die rationalen Zahlen (zwischen 0 und 1, das ist aber keine wesentliche Einschränkung der Aussage) und die natürlichen Zahlen stehen in einer Eins-zu-Eins-Beziehung.
Damit ist die Kontinuumshypothese ein prominentes Beispiel für den Gödelschen Unvollständigkeitssatz, nach dem es in der Mathematik immer Aussagen geben wird, die weder beweisbar, noch widerlegbar sind.
 Kurt Gödel, (* 28. April 1906 in Brünn, Österreich-Ungarn, heute Tschechien; † 14. Januar 1978 in Princeton, New Jersey, Vereinigte Staaten)
Kurt Gödel, (* 28. April 1906 in Brünn, Österreich-Ungarn, heute Tschechien; † 14. Januar 1978 in Princeton, New Jersey, Vereinigte Staaten)
Problem 2: Sind die Axiome der Arithmetik widerspruchsfrei?
Antwort: Antwort: Die Widerspruchsfreiheit der Axiome der Arithmetik lässt sich nicht innerhalb der Arithmetik beweisen, allerdings ist ein Beweis mit stärkeren Systemen, wie ZFC möglich.
Giuseppe Peano stellte 1889 ein System von Axiomen vor, welches die Menge der natürlichen Zahlen charakterisiert und das Rechnen mit ihnen in einem streng logischen Rahmen beschreibt – und kommt dabei nur mit den Begriffen Null, Nachfolger und fünf grundlegenden Regeln, die diese Begriffe in Beziehung setzen aus (eine davon ist zum Beispiel „Null ist kein Nachfolger“). Addition und Multiplikation werden dann über den Begriff des Nachfolgers definiert.
 Giuseppe Peano (* 27. August 1858 in Spinetta, heute Teil von Cuneo, Piemont; † 20. April 1932 in Turin)
Giuseppe Peano (* 27. August 1858 in Spinetta, heute Teil von Cuneo, Piemont; † 20. April 1932 in Turin)
Auf diese Weise entsteht ein ungeahnt mächtiges System, das in der Lage ist, eine Fülle von Aussagen der Arithmetik zu beweisen, wie zum Beispiel auch die Existenz und Eindeutigkeit der Primfaktorzerlegung.
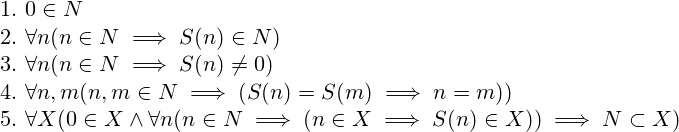 Die fünf Peano-Axiome: 1. 0 ist eine natürliche Zahl, 2. Zu jeder natürlichen Zahl gibt es eine „Nachfolger“ genannte Zahl, 3. 0 ist nicht Nachfolger einer natürlichen Zahl. 4. Wenn zwei natürliche Zalen den gleichen Nachfolger haben, sind sie gleich. 5. Eine Menge, die 0 enthält und mit jeder natürlichen Zahl auch ihren Nachfolger, enthält alle natürlichen Zahlen; dieses Axiom stellt sicher, dass die Beweismethode der vollständigen Induktion anwendbar ist.
Die fünf Peano-Axiome: 1. 0 ist eine natürliche Zahl, 2. Zu jeder natürlichen Zahl gibt es eine „Nachfolger“ genannte Zahl, 3. 0 ist nicht Nachfolger einer natürlichen Zahl. 4. Wenn zwei natürliche Zalen den gleichen Nachfolger haben, sind sie gleich. 5. Eine Menge, die 0 enthält und mit jeder natürlichen Zahl auch ihren Nachfolger, enthält alle natürlichen Zahlen; dieses Axiom stellt sicher, dass die Beweismethode der vollständigen Induktion anwendbar ist.
Hilberts zweites Problem fragt nun danach, ob innerhalb der Peanoarithmetik das Herleiten von Widersprüchen ausgeschlossen werden kann. Gödel zeigte mit seinem Unvollständigkeitssatz, dass der Beweis einer solchen Widerspruchsfreiheit im Rahmen der Peanoaxiome nicht möglich ist. 1936 zeigte Gentzen aber mit seinem Konsistenzsatz, dass die Peanoarithmetik innerhalb des wesentlich stärkeren ZFC, dem heutigen Standardaxiomensystem der Mengenlehre, keine Widersprüche hervorruft. Die Zermelo-Fraenkel-Mengenlehre (ZFC) ist eine verbreitete axiomatische Mengenlehre, die nach Ernst Zermelo und Abraham Adolf Fraenkel benannt ist.
Hilberts zweites Problem ist, ähnlich wie bereits das erste, ein Beispiel dafür, dass der Wahrheitsgehalt mathematischer Aussagen davon abhängen können, welche Grundannahmen (Axiome) man beim Beweis eines Theorems zu Grunde legt: Sätze, die in dem einen Axiomensystem falsch oder nicht entscheidbar sind, können mit zusätzlichen Annahmen entscheidbar und sogar wahr sein.
Problem 3: Sind zwei Körper (genauer: Polyeder), zum Beispiel ein Würfel und ein Tetraeder, zerlegungsgleich, wenn Sie das gleiche Volumen besitzen?
Antwort: Nein.
Zwei Körper heißen zerlegungsgleich, wenn man einen der beiden Körper mit geraden Schnitten in endlich viele Teile zerteilen kann und aus diesen Teilen den anderen Körper zusammensetzen kann. Offenbar müssen zerlegungsgleiche Körper das gleiche Volumen haben. Hilberts drittes Problem stellt die Frage, ob diese Bedingung auch hinreichend ist, also ob zwei volumengleiche Körper auch zerlegungsgleich sind. In zwei Dimensionen ist die Aussage wahr, das heißt, dass flächengleiche Figuren mit Zerschneiden, Drehen und Bewegen stets ineinander überführbar sind.
 Wenn zwei Figuren in der Ebene den gleichen Flächeninhalt haben, kann man sie immer durch Schneiden und neu Anordnen ineinander überführen. Das ist aber alles andere als klar.
Wenn zwei Figuren in der Ebene den gleichen Flächeninhalt haben, kann man sie immer durch Schneiden und neu Anordnen ineinander überführen. Das ist aber alles andere als klar.
Bei drei und höheren Dimensionen ist eine Zerlegungsgleichheit bei gleichem Volumen im Allgemeinen allerdings nicht mehr gegeben. Der deutsche Mathematiker Max Dehn zeigte bereits 1901, also ein Jahr nach Hilberts berühmter Rede, dass Würfel und Tetraeder nicht zerlegungsgleich sind. Dafür definierte Dehn die nach ihm benannte Dehninvariante eines Körpers, eine Größe, die sich bei einer Zerlegung und Neuanordnung eines Körpers nicht ändert und zeigte dann, dass Tetraeder und Würfel unterschiedliche Dehninvarianten haben, also nicht zerlegungsgleich sein können.
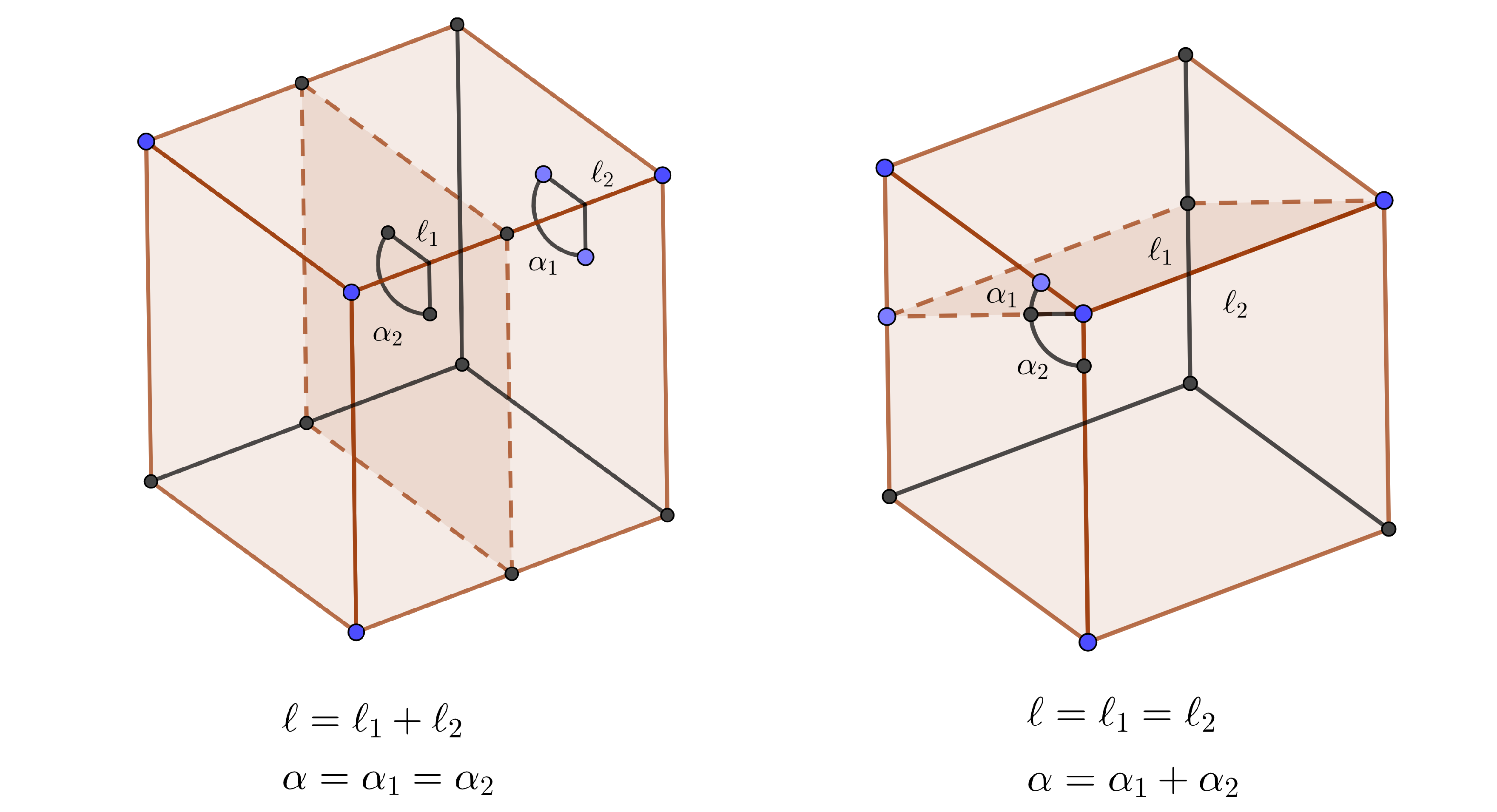 Dehn erkannte, dass es nur zwei verschiedene Arten der Zerlegung von Körpern gibt: Solche, bei denen die Winkel und die Summe der Kantenlängen gleichbleiben und solche, bei denen die Kantenlängen und die Summe der Winkel gleichbleiben. Aus diesen Daten konstruierte er dann eine Größe, die unter jedem Schnitt gleichbleibt.
Dehn erkannte, dass es nur zwei verschiedene Arten der Zerlegung von Körpern gibt: Solche, bei denen die Winkel und die Summe der Kantenlängen gleichbleiben und solche, bei denen die Kantenlängen und die Summe der Winkel gleichbleiben. Aus diesen Daten konstruierte er dann eine Größe, die unter jedem Schnitt gleichbleibt.
1963 zeigte Sydler, dass Volumen und Dehninvariante zerlegungsgleiche Körper vollständig charakterisieren: Körper, die volumengleich sind und eine gleiche Dehninvariante haben, sind demnach stets zerlegungsgleich.
Problem 4: Wie lassen sich Metriken charakterisieren, in denen alle Geraden Geodäten sind?
Antwort: Das Problem ist zu vage gestellt, als dass es eine zufriedenstellende Antwort geben kann.
Über 2000 Jahre war die euklidische Geometrie, also die klassische Geometrie, in der insbesondere das Parallelenpostulat, nach dem es zu jeder Gerade und jedem Punkt, der nicht auf diese Gerade liegt stets genau eine zu dieser Geraden parallele Gerade gibt, die den gegebenen Punkt enthält, der Inbegriff der Geometrie. Bis schließlich Anfang des 19. Jahrhunderts die Mathematiker János Bolyai, Nikolai Lobatschewski und Carl Friedrich Gauß begannen, eine nichteuklidische Geometrie zu entwickeln, also eine, in der das Parallelenpostulat nicht gilt, wie beispielsweise die Geometrie auf der Oberfläche einer Kugel, die keine Parallelen kennt.
 Auf der Oberfläche einer Kugel übernehmen Großkreise, also Kreise deren Mittelpunkte der Mittelpunkt der Kugel sind. Hier gibt es keine paralalle Geraden (Abb.: Freie Lizenz)
Auf der Oberfläche einer Kugel übernehmen Großkreise, also Kreise deren Mittelpunkte der Mittelpunkt der Kugel sind. Hier gibt es keine paralalle Geraden (Abb.: Freie Lizenz)
Dies war eine Anfangsstunde der modernen Geometrie, die in der Folgezeit eine gleichberechtigte und eigenständige Disziplin neben der Analysis und der Algebra werden sollte. Insbesondere entwickelten unter anderem Jacob Steiner und Hilbert Ende des 19. Jahrhunderts die synthetische Geometrie, die versucht, Begriffe wie Punkte und Geraden, und ihre Beziehungen zueinander rein axiomatisch zu begründen, ohne dabei auf den Anschauungsraum Bezug zu nehmen. Hilbert soll einmal zu seinem Axiomensystem der euklidischen Geometrie bemerkt haben, dass man anstelle der Begriffe Gerade, Punkt und Ebene genauso gut auch Tische, Stühle und Bierseidel verwenden könne.
 In der Hyperbolischen Geometrie, wie sie etwa auf der Oberfläche von Kartoffelchips existiert, gibt es zu jeder Gerade und jedem Punkt unendlich viele Parallelen, die durch den Punkt verlaufen (Abb. Freie Lizenz).
In der Hyperbolischen Geometrie, wie sie etwa auf der Oberfläche von Kartoffelchips existiert, gibt es zu jeder Gerade und jedem Punkt unendlich viele Parallelen, die durch den Punkt verlaufen (Abb. Freie Lizenz).
Die kürzesten Verbindungen zwischen zwei Punkten in einem Raum nennt man Geodäten; in der euklidischen Geometrie sind die Geodäten genau die Geradenstücke zwischen Punkten; eine Tatsache, die auch in manchen nichteuklidischen Geometrien Bestand hat, wie beispielsweise auf der oben erwähnten Kugeloberfläche, bei der die Geraden die Kreise um den Kugelmittelpunkt darstellen. Das 4. Hilbertsche Problem stellt die Frage, in welchen Geometrien, insbesondere abgesehen von der euklidischen Geometrie, diese Feststellung immer noch gilt.
 Georg Hamel (* 12. September 1877 in Düren; † 4. Oktober 1954 in Landshut)
Georg Hamel (* 12. September 1877 in Düren; † 4. Oktober 1954 in Landshut)
In seiner 1903 veröffentlichten Dissertation gelang es Hamel, einem Schüler von Hilbert, eine Vielzahl solcher Geometrien anzugeben; da Hamel aber Methoden der Variationsrechnung, also Methoden der Analysis, benutzte, galt das Ergebnis im Sinne der synthetischen Geometrie als nicht zufriedenstellend. Mit dem Problem beschäftigten sich danach unter anderem Herbert Buseman und der Russe Alexei Wassiljewitsch Pogorelow, der 1979 eine Monographie über das vierte Problem veröffentlichte.
Problem 5: Ist eine lokal euklidische, topologische Gruppe eine Lie-Gruppe, bei der also die Gruppenoperationen auch differenzierbar sind?
Antwort: Ja.
Gruppen beschreiben in der Mathematik Symmetrien – oder, genauer – Symmetrieoperationen, wie Spiegeln, Verschieben oder Drehen. Dabei können viele derartige Operationen selbst als geometrische Objekte aufgefasst werden: Die Menge aller Drehungen um eine Achse kann zum Beispiel mit einem Kreis identifiziert werden, während die Menge aller Verschiebungen in eine feste Richtung einer Geraden entspricht.
 Den Symmetrieoperationen eines Kegels (also Drehungen) entsprechen einem Kreis.
Den Symmetrieoperationen eines Kegels (also Drehungen) entsprechen einem Kreis.
Gruppen, die in dieser Art selbst als geometrische Objekte aufgefasst werden können, nennt man lokaleuklidisch, sie sehen lokal stets so aus wie der endlichdimensionale euklidische Anschauungsraum. Die typischsten Vertreter der Klasse der lokaleuklidischen Gruppen haben eine glatte Oberfläche in dem Sinne, dass sie keine Knicke aufweisen und dass die Hintereinanderausführung der Operationen auch hinreichend glatt ist; solche Gruppen heißen Lie-Gruppen, benannt nach dem norwegischen Mathematiker Sophus Lie. Hilberts fünftes Problem fragt nun danach, ob alle lokaleuklidischen Gruppen bereits Lie-gruppen sind, das heißt, grob gesprochen, dass aus der Stetigkeit der betrachteten Symmetrieoperation auch folgt, dass diese Symmetrieoperationen glatt verlaufen. Nachdem zuvor nur Spezialfälle, wie der Fall, bei dem die Symetrieoperationen vertauschbar sind, gelöst wurden, gelang es Andrew Gleason, Deane Montgomery und Leo Zippin in den 1950er Jahren die endgültige Klärung des Problems.
 Andrew Gleason (* 4. November 1921 in Fresno, Kalifornien; † 17. Oktober 2008 in Cambridge (Massachusetts))
Andrew Gleason (* 4. November 1921 in Fresno, Kalifornien; † 17. Oktober 2008 in Cambridge (Massachusetts))
Durch die Entwicklung der abstrakten Harmonischen Analysis durch die Einführung des Haar-Integrals und der Sätze von Pontryargin und Peter-Weyl rückte eine weitere wichtige Teilklasse der topologischen Gruppen in den Blick: Die Klasse der lokalkompakten Gruppen: topologische Gruppen, die eine in einem gewissen Sinne überschaubare (kompakte) Umgebung haben; insbesondere ist jede Lie-Gruppe eine lokalkompakte Gruppe. Viele Konzepte aus der Analysis und der Funktionalanalysis, darunter auch die Theorie der Fourieranalyse (die zu Fouriers Zeiten eine Art Zerlegungstheorie von Schwingungen war), lassen sich auf lokalkompakte Gruppen ausdehnen. Für lokaleuklidische Gruppen bewies der Japaner Hidehiko Yamabe 1953, dass es zwar lokalkompakte Gruppen gibt, die keine Lie-Gruppen sind, jedoch aber jede lokalkompakte Gruppe "in guter Näherung" eine Lie-Gruppe ist (jede lokalkompakte Gruppe ist projektiver Limes von Lie-Gruppen).
 Leo Zippin (* 25. Januar 1905 in New York City; † 11. Mai 1995 ebenda)
Leo Zippin (* 25. Januar 1905 in New York City; † 11. Mai 1995 ebenda)
Lokaleuklidische (oder allgemeiner: topologische) Gruppen sind auch heute noch Forschungsgegenstand in vielen Teilen der Mathematik. Bemerkenswert ist dabei die Vielfalt der Methoden, die zum Studium topologischer Gruppen benutzt wird und die Vielfalt der Perspektiven, unter denen man sie betrachtet: Ist man etwa in der Differentialgeometrie daran interessiert, sie als geometrische Objekte zu verstehen, betrachtet man sie in der Topologie hingegen oftmals bezüglich ihrer Wirkungen auf Räume. In der harmonischen Analysis studiert man topologische Gruppen wiederum, indem man die Funktionen auf ihnen untersucht, um dadurch gegebenenfalls Rückschlüsse auf ihre Struktur zu ziehen. Topologische Gruppen gehören daher zu den Brückenelementen, über die unterschiedliche Bereiche der Mathematik miteinander verbunden werden können.
Problem 6: Wie kann die Physik axiomatisiert werden?
Antwort: Die Physik hat mit der Entwicklung der Quantenmechanik und der allgemeinen Relativitätstheorie gewaltige Fortschritte gemacht; vor diesem Hintergrund ist der Versuch einer Axiomatisierung der gesamten Physik weder zweckmäßig noch sinnvoll.
Die rasante Entwicklung und Mathematisierung der spätklassischen Physik beschäftigte auch Hilbert, den die Arbeiten von Mach, Hertz und insbesondere Boltzmann, dem es erstmals gelang, die Thermodynamik rein nach den Lehren der klassischen Mechanik zu beschreiben, tief beeindruckten. Zur Jahrhundertwende waren die Phänomene der klassischen Physik (also die Physik ohne Relativitätstheorie und Quantenmechanik) gut untersucht und konnten in der Mechanik durch Newton und Lagrange, in der Elektrodynamik durch Maxwell und in der Thermodynamik durch Boltzmann in geschlossener Form durch mathematische Gleichungen beschrieben werden.
 Ludwig Boltzmann (* 20. Februar 1844 in Wien; † 5. September 1906 in Duino, Österreich-Ungarn)
Ludwig Boltzmann (* 20. Februar 1844 in Wien; † 5. September 1906 in Duino, Österreich-Ungarn)
Hilbert, dem Mathematiker und vor allem Formalisten, genügte die Beschreibung der physikalischen Phänomene durch mathematische Gleichungen allerdings nicht; ihm schwebte eine Physik ganz im Sinne seiner Axiomatisierung der euklidischen Geometrie vor, deren Gesetze sich rein logisch und widerspruchsfrei aus Grundannahmen herleiten ließen. Hilbert konnte zum Zeitpunkt seiner Rede noch nicht wissen, dass die Physik wenige Jahrzehnte später durch die Relativitätstheorie und die Quantenmechanik eine Revolution erleben würde, die vermutlich in ihrer Geschichte einmalig ist. Dennoch findet Hilberts Ansinnen auch in der neuen, nichtklassischen Physik, wenn auch unter deutlich erschwerten Umständen, seinen Platz: So gab und gibt es in der Quantenmechanik Versuche der Axiomatisierung, wie das Beispiel der Whiteman- oder der Osterwalder-Schrader-Axiome zeigt.
Problem 7: Ist die Potenz \(\alpha ^\beta\) immer transzendent, wenn \(\alpha\) algebraisch \(\alpha \neq 0,\alpha \neq 1\) und \(\beta\) irrational und algebraisch ist?
In der Algebra und in der alebraischen Zahlentheorie ist die Frage nach der Transzendenz einer Zahl von herausragender Bedeutung. Eine Zahl heißt transzendent, wenn sie nicht algebraisch ist, also nicht als Lösung einer Polynomialgleichung darstellbar ist. Transzendenz ist ein schärferer Begriff als Irrationalität, jede transzendente Zahl ist irrational, aber nicht jede irrationale Zahl ist transzendent. Beispielsweise ist \(\sqrt {2}\) als Lösung der Gleichung \(x^ 2- 2=0\) zwar irrational, aber nicht transzendent.
 Die Konstanten e, \pi und \sqrt{2}. Die ersten beiden sind transzendent, \sqrt{2} ist zwar irrational, aber algebraisch.
Die Konstanten e, \pi und \sqrt{2}. Die ersten beiden sind transzendent, \sqrt{2} ist zwar irrational, aber algebraisch.
Cantor bewies mit einer Variation seines zweiten Diagonalarguments zwar, dass nur abzählbar viele algebraische Zahlen überabzählbar vielen transzendenten Zahlen gegenüber stehen müssen, allerdings war es bis dahin (und ist es auch heute) bei vielen Zahlen unbekannt, ob sie transzendent oder algebraisch sind. Zwar konstruierte Liouville 1844 erstmals eine transzendente Zahl, (die nach ihm benannte Liouville-Zahl) und Lindemann zeigte 1882 die Transzendenz für \(e\) und \(\pi\). Ein Verfahren aber, mit dem man nach Belieben eine große Menge neuer transzendenter Zahlen, die sich in ihrer Konstruktion wesentlich unterschieden, liefern konnte, fehlte.
 Joseph Liouville (* 24. März 1809 in Saint-Omer; † 8. September 1882 in Paris)
Joseph Liouville (* 24. März 1809 in Saint-Omer; † 8. September 1882 in Paris)
Mit dem Beweis des siebten Problems durch Alexander Gelfond hatte man nun eine Vielzahl von Beispielen für transzendente Zahlen zur Hand. Dennoch weiß man bei vielen Zahlen bis heute nicht, ob sie transzendent sind oder nicht. Prominente Beispiele hierfür wären \(e+\pi\), \(e\cdot \pi\) und \(\zeta(3)\), wobei \(\zeta\) die Riemannsche Zeta-Funktion ist. Dadurch gehören Transzendenzvermutungen auch heute noch zu jenen offenen Fragen, die auch mathematischen Laien zugängig sind.
 Theodor Schneider (* 7. Mai 1911 in Frankfurt am Main; † 31. Oktober 1988 in Freiburg im Breisgau)
Theodor Schneider (* 7. Mai 1911 in Frankfurt am Main; † 31. Oktober 1988 in Freiburg im Breisgau)
Problem 8: Besitzen alle nichttrivialen Nullstellen der Riemannschen Zetafunktion den Realteil \(\frac{1}{2}\)?
Antwort: unbekannt
Das achte Problem auf Hilberts Liste ist die berühmte Riemannsche Vermutung; sie ist das einzige Problem, das auch in der Liste der Milleniumsprobleme auftaucht und gilt vielen als der heilige Gral der Mathematik. Sie ist bis heute ungelöst. Die Riemannsche Vermutung fragt nach den Nullstellen der Riemannschen Zeta-Funktion, das ist die Funktion \(\zeta(s)=\sum_{n=1}^\infty \frac{1}{n^s}\), ausgeweitet auf den Bereich der komplexen Zahlen. Die Riemann-Vermutung (auch Riemann-Hypothese genannt) besagt, dass alle Nullstellen, deren Realteil zwischen 0 und 1 liegt, den Realteil \(\frac{1}{2}\) haben. Hinter dieser willkürlich wirkenden Behauptung verbirgt sich eines der größten Rätsel der Mathematik – die Verteilung der Primzahlen.
 Graphische Darstellung der Zeta-Funktion. Die Nullstellen, deren Realteil nicht 0 ist, scheinen alle auf einer vertikalen Geraden zu liegen. Aber ob dem auch wirklich so ist, ist unbekannt.
Graphische Darstellung der Zeta-Funktion. Die Nullstellen, deren Realteil nicht 0 ist, scheinen alle auf einer vertikalen Geraden zu liegen. Aber ob dem auch wirklich so ist, ist unbekannt.
Bereits Euler hat mit dem Beweis des sog. Eulerproduktes einen tiefen Zusammenhang zwischen den Primzahlen auf der einen und der Zeta-Funktion auf der anderen Seite gefunden, der von Riemann in seinem wegweisenden Aufsatz über die Verteilung der Primzahlen unter einer gegebenen Größe noch erweitert wurde. Er verknüpfte dabei Resultate aus der Funktionentheorie und der Zahlentheorie auf ungeahnte Weise, indem er einen Zusammenhang zwischen der Verteilung der Primzahlen und den Nullstellen der Zetafunktionen aufzeigte.
 Auszug aus Riemanns wegweisender Arbeit. Auf dieser Seite ist die Riemannhypothese formuliert ([…]hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrlich schien […])
Auszug aus Riemanns wegweisender Arbeit. Auf dieser Seite ist die Riemannhypothese formuliert ([…]hiervon wäre allerdings ein strenger Beweis zu wünschen; ich habe indess die Aufsuchung desselben nach einigen flüchtigen vergeblichen Versuchen vorläufig bei Seite gelassen, da er für den nächsten Zweck meiner Untersuchung entbehrlich schien […])
Das daraus entstandene Fachgebiet heißt, in Abgrenzung zur algebraischen Zahlentheorie, analytische Zahlentheorie. Die Riemannsche Vermutung ist dabei so fundamental, dass zahlreiche Sätze der analytischen Zahlentheorie nur unter Voraussetzung der Riemann-Hypothese wahr sind, das heißt, dass diese Sätze mit dem Passus „unter Voraussetzung der Riemann-Hypothese gilt:“ beginnen. Von diesen Sätzen gibt es wiederum viele, die sogar äquivalent zur Riemann-Hypothese sind, wie zum Beispiel die Vermutung von Koch, die, sollte die Riemann-Hypothese wahr sein, eine sehr präzise Abschätzung der Verteilung der Primzahlen erlaubt. Ein Beweis der Riemann-Hypothese würde daher nicht nur Licht ins Dunkel der Verteilung der Primzahlen bringen, sondern würde auch zahlreiche Probleme auf einen Schlag lösen. Bis heute ist die Riemann-Vermutung trotz zahlloser Beweisversuche ungelöst.
 Bernhard Riemann (* 17. September 1826 in Breselenz bei Dannenberg (Elbe); † 20. Juli 1866 in Selasca bei Verbania am Lago Maggiore)
Bernhard Riemann (* 17. September 1826 in Breselenz bei Dannenberg (Elbe); † 20. Juli 1866 in Selasca bei Verbania am Lago Maggiore)
Es gibt zahlreiche Verallgemeinerungen und Analoga der Riemann-Hypothese, von denen vermutlich die Weil-Vermutungen, die, grob gesagt, das Analogon der Riemann-Hypothese für endliche Körper darstellen, zu den wichtigsten gehören. Die Weil-Vermutungen wurden in der zweiten Hälfte des zwanzigsten Jahrhunderts von der Mathematikerschule um Alexander Grothendieck bewiesen und gelten als eines der wichtigsten Resultate der arithmetischen Geometrie.
Problem 9: Wie kann das quadratische Reziprozitätsgesetz verallgemeinert werden?
Antwort: Das Reziprozitätsgesetz von Artin gilt als weitreichende Verallgemeinerung, das Problem ist allerdings zu vage gestellt.
Das quadratische Reziprozitätsgesetz ist ein Verfahren, mit dem man, vereinfacht gesagt, bestimmen kann, ob der Rest einer Division eine Quadratzahl ist oder nicht. Bereits Gauß ahnte, dass das quadratische Reziprozitätsgesetz, das er Aureum Theorema, das goldene Theorem, nannte, wesentlich für die zukünftige Zahlentheorie werden sollte. Mit dieser Einschätzung sollte Gauß Recht behalten – das Wesen des quadratischen Reziprozitätsgesetzes liegt in der Primfaktorzerlegung von Kreisteilungskörpern, speziellen Erweiterungen der rationalen Zahlen.
 Deckblatt von Disquisitiones Arithmeticae von Gauß. Das Schlüsselwerk Gauß‘ gilt als eine der ersten rein zahlentheoretischen Arbeiten der Neuzeit und ist in seiner Tiefe und seinem Abstraktionsgrad seiner Zeit weit voraus. Hier gibt Gauß unter anderem mehrere Beweise für das quadratische Reziprozitätsgesetz an.
Deckblatt von Disquisitiones Arithmeticae von Gauß. Das Schlüsselwerk Gauß‘ gilt als eine der ersten rein zahlentheoretischen Arbeiten der Neuzeit und ist in seiner Tiefe und seinem Abstraktionsgrad seiner Zeit weit voraus. Hier gibt Gauß unter anderem mehrere Beweise für das quadratische Reziprozitätsgesetz an.
Gauß lieferte mehrere Beweise für das quadratische Reziprozitätsgesetz und formulierte, zusammen mit Eisenstein, Reziprozitätsgesetze höheren Grades. Das quadratische Reziprozitätsgesetz ist eines der grundlegendsten Aussagen der algebraischen Zahlentheorie, die in den Jahrzehnten vor Hilberts Rede unter anderem durch Kummer, Hensel, Frobenius und Kronecker beispielsweise durch die Entdeckung der p-adischen Zahlen oder der Formulierung der Klassenkörpertheorie sowohl im Abstraktionsgrad, als auch in den Resultaten gewaltige Fortschritte machte. Diese Entwicklung machte auch vor dem quadratischen Reziprozitätsgesetz nicht halt, das, unter anderem im Rahmen der Kummertheorie, verallgemeinert wurde; insbesondere beschränkten die Zahlentheoretiker sich nicht mehr nur auf Kreisteilungskörper, sondern auf wesentlich allgemeinere Erweiterungen der rationalen Zahlen. In Hilberts Sinne zufriedenstellend konnte Artin das quadratische Reziprozitätsgesetz verallgemeinern.
 Emil Artin (* 3. März 1898 in Wien; † 20. Dezember 1962 in Hamburg)
Emil Artin (* 3. März 1898 in Wien; † 20. Dezember 1962 in Hamburg)
Das Artin‘sche Reziprozitätsgesetz wiederum ist einer der Ausgangspunkte des sogenannten Langlandsprogramms, ein gewaltiges Forschungsprogramm in der modernen Mathematik, dass die arithmetische Geometrie, wie dieser Teil der Zahlentheorie heute heißt, wesentlich geprägt hat.
Problem 10: Man gebe ein Verfahren an, das für eine beliebige diophantische Gleichung entscheidet, ob sie lösbar ist.
Antwort: Es gibt kein solches Verfahren.
Diophantische Gleichungen sind Polynomialgleichungen, bei denen nur ganzzahlige oder bestenfalls rationale Lösungen zugelassen sind. Diese Zusatzbedingung sorgt dafür, dass die diophantischen Gleichungen und ihre Lösungen ungleich schwerer zu handhaben sind als ihre in der algebraischen Geometrie untersuchten Pendants, die klassischen Polynomialgleichungen. Die wohl bekannteste Menge diophantischer Gleichungen sind diophantischen Gleichungen \(x^n+y^n=z^n\), wobei die Frage nach der Existenz von Lösungen für die Fälle \(n>2\) als Fermatsche Vermutung in die Mathematikgeschichte einging. Die Fermatsche Vermutung blieb über drei Jahrhunderte ungeklärt, bis schließlich Andrew Wiles das Problem im Jahr 1993 lösen konnte.
 Pythagoräische Tripel sind Zahlentripel ganzer Zahlen, \(x,y\) und \(z\), für die \(x^2+y^2=z^2\). Es geht dabei also um Punkte mit ganzzahligen Koordinaten, die auf Kreisen mit ganzzahligen Radius \(z\) liegen. Man erhält alle Pythagoräischen Tripel, indem man für beliebige ganze Zahlen \(a\) und \(b\) berechnet: \(x=a^2-b^2\), \(y=2ab\), und \(z=a^2+b^2\). Für Exponenten größer als 2 gibt es, abgesehen von trivialen Lösungen mit Einsen und Nullen, keine weiteren Lösungen. Dies wurde von Fermat im 17. Jahrhundert vermutet und erst 300 Jahre später bewiesen.
Pythagoräische Tripel sind Zahlentripel ganzer Zahlen, \(x,y\) und \(z\), für die \(x^2+y^2=z^2\). Es geht dabei also um Punkte mit ganzzahligen Koordinaten, die auf Kreisen mit ganzzahligen Radius \(z\) liegen. Man erhält alle Pythagoräischen Tripel, indem man für beliebige ganze Zahlen \(a\) und \(b\) berechnet: \(x=a^2-b^2\), \(y=2ab\), und \(z=a^2+b^2\). Für Exponenten größer als 2 gibt es, abgesehen von trivialen Lösungen mit Einsen und Nullen, keine weiteren Lösungen. Dies wurde von Fermat im 17. Jahrhundert vermutet und erst 300 Jahre später bewiesen.
Wie bei klassischen Polynomialgleichungen ist man innerhalb der Theorie der diophantischen Gleichungen im Wesentlichen an Lösungen interessiert, die es aber, wie das Problem der Fermatschen Vermutung zeigt, in sich haben können.
 Lösungen der Pell’schen Gleichungen \(x^2-dy^2=1\), für d=2,3,5. Die gestrichelten Linien sind die Mengen der Zahlenpaare, die diese Gleichung erfüllen, ganzzahlige Lösungen sind mit Kreuzen markiert.
Lösungen der Pell’schen Gleichungen \(x^2-dy^2=1\), für d=2,3,5. Die gestrichelten Linien sind die Mengen der Zahlenpaare, die diese Gleichung erfüllen, ganzzahlige Lösungen sind mit Kreuzen markiert.
Zu Hilberts Zeiten und bis heute gab es nur wenige Beispiele für Klassen von diophantischen Gleichungen, die eine vollständige Lösungstheorie besitzen. Hilbert hat daher der Entwicklung von Lösungsalgorithmen bzw. dem Beweis der Existenz von Lösungen eine hohe Bedeutung beigemessen. Die Träume von einer positiven Lösung des 10. Problem wurden aber 1970 vom damals 23-jährigen Russen Juri Wladimirowitsch Matijassewitsch zunichte gemacht, als dieser zeigte, dass es keinen Algorithmus geben kann, der zu einer gegebenen diophantischen Gleichung entscheidet, ob sie lösbar ist.
 Juri Wladimirowitsch Matijassewitsch (* 2. März 1947 in Leningrad)
Juri Wladimirowitsch Matijassewitsch (* 2. März 1947 in Leningrad)
Überraschenderweise war das Ergebnis Matijassewitschs eng verknüpft mit Fragen aus der theoretischen Informatik, die seinerzeit noch in ihren Kinderschuhen steckte. Genauer vermutete die Mathematkerin Julia Robinson, nach Vorarbeiten von Martin Davis und Hilary Putnam, dass die Lösungsmengen diophantischer Gleichungen genau die rekursiv aufzählbaren Mengen sind, also Mengen natürlicher Zahlen, für die es einen Algorithmus gibt, der sie aufzählen kann. Robinsons Vermutung wurde dann von Matijassewitsch mit Hilfe eines Systems bestehend aus zehn Gleichungen und 15 Ungleichungen bewiesen.
 Julia Robinson (* 8. Dezember 1919, in St. Louis in Missouri; † 30. Juli 1985 in Oakland, Kalifornien)
Julia Robinson (* 8. Dezember 1919, in St. Louis in Missouri; † 30. Juli 1985 in Oakland, Kalifornien)
Problem 11: Wie kann die Theorie der quadratischen Formen auf beliebige Zahlkörper verallgemeinert werden?
Antwort: Die Theorie wurde im 20 Jahrhundert umfangreich ausgebaut.
Unter einer quadratischen Form versteht man einen Ausdruck der Form \(x^\top A x\), wobei \(x\) ein Vektor und \(A\) eine symmetrische Matrix ist. Eine quadratische Form in zwei Variablen hat also beispielsweise die Darstellung \(q(x,y)=ax^2+bxy+cy^2\). Geometrisch sind quadratische Formen eng verwandt mit den Kegelschnitten (also Kreise, Parabeln, Hyperbeln und Ellipsen) in projektiven Räumen, also Räumen, die durch die Hinzunahme von unendlich fernen Punkten gewonnen werden.
 Kegelschnitte. Abbildung aus einem Lehrbuch des ausgehenden 19. Jahrhunderts.
Kegelschnitte. Abbildung aus einem Lehrbuch des ausgehenden 19. Jahrhunderts.
Erlaubt man als Variablen und Koeffizienten nicht mehr nur reelle oder komplexe Zahlen, sondern beschränkt sich auf rationale Zahlen, gelangt man zu der Theorie der quadratischen Formen über den rationalen Zahlen, die, wegen der fehlenden Vollständigkeit (man kann, anders als im reellen Fall Lösungen nicht mehr annähern), ungleich schwieriger ist. Benutzt man anstelle rationaler Zahlen Zahlkörper, also endliche Erweiterungen der rationalen Zahlen um Nullstellen von Polynomen, befindet man sich in dem für Hilberts elftes Problem relevanten Fall. Die auf Minkowski zurückgehende Lösungstheorie für den Zahlkörperfall war eine der ersten Anwendungen des in der modernen Zahlentheorie wichtigen Lokal-Global-Prinzips.
 Hermann Minkowski (* 22. Juni 1864 in Aleksotas, Russisches Kaiserreich, heute Kaunas, Litauen; † 12. Januar 1909 in Göttingen)
Hermann Minkowski (* 22. Juni 1864 in Aleksotas, Russisches Kaiserreich, heute Kaunas, Litauen; † 12. Januar 1909 in Göttingen)
Bei dieser Beweismethode zeigt man, grob gesprochen, dass eine Gleichung (oder ein System von Gleichungen) dann eine Lösung in einem Zahlkörper hat, wenn das System Lösungen in allen Vervollständigungen des Körpers hat; wobei man sich die Vervollständigung eines Körpers dabei vorstellen kann wie das Stopfen von Löchern, sodass jede Folge, in der sich Folgenglieder beliebig nahe kommen, auch einen Grenzwert hat; nichts anderes geschieht zum Beispiel bei der Konstruktion der reellen Zahlen, bei denen es sich um eine Vervollständigung der rationalen Zahlen handelt. Neben jener klassischen Vervollständigung werden beim Lokal-Global-Prinzip aber auch noch die exotisch anmutenden p-adischen Vervollständigungen verwendet, deren Entdeckung Ende des 19. Jahrhunderts durch Hensel die Zahlentheorie revolutionierte.
 Kurt Hensel (* 29. Dezember 1861 in Königsberg; † 1. Juni 1941 in Marburg)
Kurt Hensel (* 29. Dezember 1861 in Königsberg; † 1. Juni 1941 in Marburg)
Problem 12: Wie lässt sich der Satz von Kronecker-Weber auf beliebige Zahlkörper erweitern?
Antwort: Unbekannt.
Die Geburtsstunde der modernen algebraischen Zahlentheorie und eine der weitreichendsten Neuerungen der Mathematik überhaupt war die Galois-Theorie, die sich, in ihrer ursprünglichen Form, mit den Symmetrien, bzw. Symmetrieoperationen von Nullstellen von Polynomen beschäftigt, und die auf das Ausnahmetalent Evariste Galois zurückgeht. Später formulierten unter anderem Gauß, Eisenstein aber vor allem Dedekind die damalige Theorie endlicher algebraischer Körpererweiterungen um, indem sie statt Nullstellen Zahlenbereiche (Mathematiker reden von Körpern) betrachteten, die entstehen, wenn man die rationalen Zahlen um die Nullstellen von Polynomen erweitert. (solche erweiterten Zahlenbereiche heißen Zahlkörper). Ein Beispiel für eine solche Körpererweiterung ist die Menge \( \mathbb{Q}(\sqrt{2}) =\{a+b\sqrt{2} \ | \ a,b \in \mathbb{Q} \}\), bei der die rationalen Zahlen um die Nullstelle des Polynoms \(x^2-2=0\) erweitert wurde.
 Evariste Galois, (* 25. Oktober 1811 in Bourg-la-Reine; † 31. Mai 1832 in Paris)
Evariste Galois, (* 25. Oktober 1811 in Bourg-la-Reine; † 31. Mai 1832 in Paris)
Körpererweiterungen dieser Art sind die Hauptuntersuchungsgegenstände der algebraischen Zahlentheorie. In der modernen Interpretation der Galoistheorie ist die Galois-Gruppe einer Körpererweiterung, also die Gruppe der Körperautomorphismen, das heißt die Selbstabbildungen des erweiterten Körpers, die Addition und Multiplikation erhalten, und die Elemente des Grundkörpers nicht verändern, von Interesse. Im Falle von \( \mathbb{Q}(\sqrt{2})\) wäre \[a+b\sqrt{2}\longmapsto a-b\sqrt{2}\] ein solcher Körperautomorphismus. Das Schlüsselresultat der Galois-Theorie besagt nun, dass jede algebraische Körpererweiterung durch ihre Galois-Gruppe beschrieben werden kann, genauer: Für jede algebraische Körpererweiterung gibt es eine Eins-zu-Eins-Beziehung zwischen ihrer Galois-Gruppe und den Zwischenkörpern, das heißt den Zahlenbereichen, die zwischen dem Grundkörper und dem Erweiterungskörper stehen.
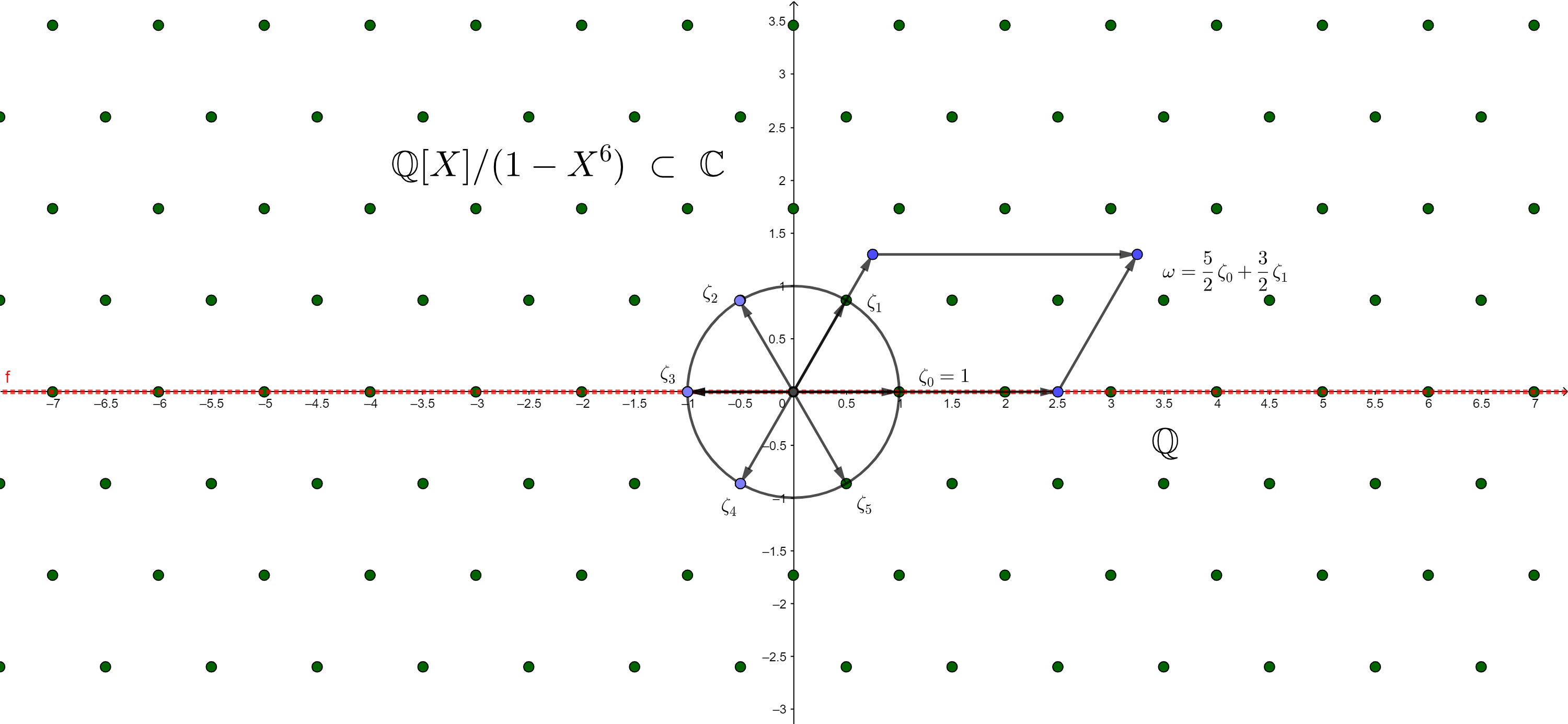 Der Kreisteilungskörper \(\mathbb{Q}[X]\left(1-X^6\right)\) besteht aus den rationalen Zahlen und allen rationalen Kombinationen der sechsten komplexen Einheitswurzeln, die mit gleichem Abstand auf dem Einheitskreis in der komplexen Zahlenebene liegen.
Der Kreisteilungskörper \(\mathbb{Q}[X]\left(1-X^6\right)\) besteht aus den rationalen Zahlen und allen rationalen Kombinationen der sechsten komplexen Einheitswurzeln, die mit gleichem Abstand auf dem Einheitskreis in der komplexen Zahlenebene liegen.
Wenn nun ein Zahlkörper eine endliche abelsche Galois-Gruppe hat, liefert der Satz von Kronecker-Weber eine besonders zufriedenstellende Darstellung des Sachverhalts: Er besagt, dass der Erweiterungskörper dann in einem Kreisteilungskörper enthalten ist. Kreisteilungskörper sind vergleichsweise leicht zu verstehende Körpererweiterungen. Sie entstehen, wenn man zu den rationalen Zahlen die Nullstellen von Polynomen der Form \(x^n-1=0\) hinzufügt (diese Gleichung hat im Komplexen \(n\) Lösungen hat).
 Leopold Kronecker (* 7. Dezember 1823 in Liegnitz; † 29. Dezember 1891 in Berlin)
Leopold Kronecker (* 7. Dezember 1823 in Liegnitz; † 29. Dezember 1891 in Berlin)
Hilberts zwölftes Problem fragt nun danach, ob vergleichbare Beziehungen, also Einbettungen von Körpererweiterungen in leichter zu verstehende Körper auch im deutlich komplizierteren Fall von unendlichen abelschen Körpererweiterungen möglich ist, also die Frage danach, durch die Hinzunahme welcher Elemente beliebige abelsche Erweiterngen der rationalen Zahlen in Gänze beschrieben werden können. Zwar konnten in den sechziger Jahren des zwanzigsten Jahrhunderts die Japaner Gorō Shimura und Yutaka Taniyama mit der Einführung der CM-Körper eine Teillösung des Problems vorstellen, aber von einer endgültigen Lösung des Problems ist man noch weit entfernt.
Problem 13: Kann die Lösung der Gleichung \(x^{7}+ax^{3}+bx^{2}+cx+1=0\) mit Hilfe einer endlichen Anzahl von stetigen Funktionen konstruiert werden, die von zwei Variablen abhängen?
Antwort: Ja.
Seit den Arbeiten von Abel und Galois war bekannt, dass Polynomgleichungen in einer Variablen für Grade größer oder gleich fünf nicht durch Radikale auflösbar sind. Das bedeutet, dass es keine der bekannten pq-Formel vergleichbaren Lösungsformeln für Polynome höheren Grades mehr gibt. Zwar kann man mit geschickten Substitutionen eine Gleichung der Form \[dx^7+ex^6+fx^4+gx^3+hx^2+ix+j=0\] in eine Gleichung der Form \[x^{7}+ax^{3}+bx^{2}+cx+1=0\] umwandeln; zu einer Lösung gelangt man dadurch allerdings nicht. Allerdings ist eine Lösung \(x\) dieser Gleichung nun eine stetige Funktion, die von nur noch drei Variablen \(a\), \(b\) und \(c\) abhängt. Hilberts 13. Problem fragt nun nach der Möglichkeit, diese Funktion mit Hilfe von endlich vielen stetigen Funktionen von zwei Variablen darzustellen, ein Verfahren, das zu Hilberts Zeiten Nomographie genannt wurde. Hilbert konnte zeigen, dass wenn man sich auf algebraische Funktionen (vereinfacht gesprochen, Funktionen, deren Funktionswerte man erhält indem man Nullstellen von Polynomen berechnet; Polynome sind algebraische Funktionen, ebenso aber auch Wurzelfunktionen und rationale Funktionen) beschränkt, das Problem nicht lösbar ist, und fragte daher auf dem Internationalen Mathematikerkongress in Paris, ob man es zumindest mit der wesentlich größeren Klasse der stetigen Funktionen lösen kann. Wesentlich vorangebracht wurde das Problem in seiner stetigen Variante durch den großen sowjetischen Mathematiker Andrei Kolmogorov, der 1956 zeigte, dass sich eine stetige Funktion von mehreren Variablen stets mit Hilfe von Funktionen dreier Variablen darstellen lässt;
 Andrei Nikolajewitsch Kolmogorow (* 12.jul./ 25. April 1903 greg. in Tambow; † 20. Oktober 1987 in Moskau)
Andrei Nikolajewitsch Kolmogorow (* 12.jul./ 25. April 1903 greg. in Tambow; † 20. Oktober 1987 in Moskau)
ein Jahr später zeigte sein damals erst neunzehnjähriger Schüler Wladimir Arnold, dass für das Resultat bereits Funktionen mit zwei Veränderlichen ausreichten und löste damit Hilberts dreizehntes Problem.
Problem 14: Sind Ringe, die im Zusammenhang mit der Invariantentheorie entstehen, endlich erzeugt?
Antwort: Nein.
Eines der am intensivsten beforschten Teilgebiete der Algebra und algebraischen Geometrie des ausgehenden 19. Jahrhunderts war die sogenannte Invariantentheorie, die sich mit der Frage beschäftigt, welche mathematische Struktur Teilmengen von Polynomen haben, deren Gestalt sich nicht ändert (invariant bleibt), wenn Gruppen auf ihnen wirken. Betrachtet man zum Beispiel die Menge \(P\) der Polynome in zwei Veränderlichen \(x\) und \(y\), so wirkt auf ihnen die Gruppe mit den Elementen \(-1\) und \(1\) in folgender Form: \(x \rightarrow -x\) und \(y\rightarrow -y\). Polynome, die unter dieser Wirkung invariant sind, sind dann alle Polynome, die von den Ausdrücken \(x^2,\ y^2\) und \(xy\) erzeugt werden, wie zum Beispiel \(x^2, yx+y^4-3x^2,\) oder \((x+y)^2=x^2+2xy+y^2\) (da "Minus mal Minus" plus ergibt). Betrachtet man statt Polynomen den Körper der rationalen Funktionen, gelangt man zu invarianten Funktionenkörpern, die den Hauptuntersuchungsgegenstand von Hilberts vierzehntem Problem bilden. Es geht dabei um die Frage, ob Ringe, die sowohl rationale invariante Funktionen, als auch Polynome sind, stets endlich erzeugt sind, das heißt, ob es in diesem Fall immer endlich viele Polynome gibt, sodass jede rationale invariante Funktion als Kombination aus solchen Basispolynomen geschrieben werden kann. Hilbert arbeitete selbst länger an diesem Problem und konnte bereits Spezialfälle lösen, und bewies den nach ihm benannten Basissatz, ein wichtiges Hilfsmittel in der Invariantentheorie und der kommutativen Algebra. Oscar Zariski, einer der großen Modernisierer der algebraischen Geometrie formulierte Hilberts vierzehntes Problem in der (moderneren) Sprache der algebraischen Varietäten und algebraischen Gruppen.
 Oscar Zariski (* 24. April 1899, in Kobryn, Weißrussland; † 4. Juli 1986 in Brookline, Massachusetts, USA)
Oscar Zariski (* 24. April 1899, in Kobryn, Weißrussland; † 4. Juli 1986 in Brookline, Massachusetts, USA)
Da mit der Zeit immer mehr Spezialfälle gelöst wurden, unter anderem durch Emmy Noether (für endliche Gruppen), Roland Weitzenböck (für sog. Parametergruppen) und Hermann Weyl (für zusammenhängende Lie-Gruppe) schien ein Beweis des allgemeinen Falls in greifbarer Nähe, bis es dem Japaner Masayoshi Nagata schließlich gelang, die Vermutung mit einem Gegenbeispiel zu widerlegen. Da sich die Aussage aus Hilberts vierzehntem Problem für viele Spezialfälle als richtig erwiesen hat, ist es wenig verwunderlich, dass Nagatas Gegenbeispiel äußerst kompliziert ist: Er benutzt dafür unter anderem Polynome in 32 Veränderlichen und 13-dimensionale Vektorräume und zeigte, dass es Ringe der obigen Gestalt gibt, die nicht endlich erzeugt sind.
 Emmy Noether, (*23. März 1882 in Erlangen; †14. April 1935 in Bryn Mawr, Pennsylvania)
Emmy Noether, (*23. März 1882 in Erlangen; †14. April 1935 in Bryn Mawr, Pennsylvania)
Die klassische algebraische Invariantentheorie ist heute etwas in Vergessenheit geraten. Die aus ihr entwachsenen Disziplinen, wie die geometrische Invariantentheorie nach Mumford, sind aber nach wie vor aktiv beforschte Teilgebiete.
Problem 15: Wie kann der Schubert-Kalkül formalisiert werden?
Antwort: Einige Fragen sind noch offen.
Der Schubert-Kalkül ist eine aus dem Gebiet der abzählenden Geometrie entstandene Disziplin, die sich mit dem Abzählen von Schnittgebilden in projektiven Räumen beschäftigt. Projektive Räume sind Räume, bei denen es neben den üblichen Punkten auch unendlich ferne Punkte gibt, in denen sich bspw. Geraden schneiden, die im klassischen, also affinen, Räumen parallel wären. Eine typische Frage im Schubert-Kalkül ist zum Beispiel: Gegeben sind vier Geraden (im projektiven Raum), von denen sich je zwei schneiden. Wie viele Geraden existieren, die alle vier Geraden schneiden? Man kann zeigen, dass es genau zwei solcher Geraden gibt, nämlich die Gerade durch die Schnittpunkte, sowie die Schnittgerade der von je zwei sich schneidenden Geraden aufgespannten Ebenen.
 Wie viele Geraden gibt es, die alle vier geraden mindestens einmal schneiden? Genau zwei: Die Gerade zwischen den beiden Schnittpunkten (rot) und die Schnittgerade der Ebenen ABCD und EFGH (grün).
Wie viele Geraden gibt es, die alle vier geraden mindestens einmal schneiden? Genau zwei: Die Gerade zwischen den beiden Schnittpunkten (rot) und die Schnittgerade der Ebenen ABCD und EFGH (grün).
Hermann Schubert bemerkte in den 1870er Jahren, dass man mit den geforderten Bedingungen an die geometrischen Objekte in einem gewissen Sinne rechnen kann (daher der Name Kalkül von lat. calculare, berechnen), das heißt, dass man zwei oder mehrere Bedingungen zu einer neuen verknüpfen kann, und man auf diese Weise Abzählungskriterien für Schnittgebilde-Probleme erhält. Es entstand so eine Theorie, der Schubert-Kalkül, die später von italienischen Geometern um Francesco Severi aufgegriffen wurde. Der Schubert-Kalkül wurde allerdings nie, obwohl er stets richtige Vorhersagen machte, als Theorie streng bewiesen, weder von Schubert, noch von der Schule Severi, die für ihre Beweise auch heuristische Stetigkeitsargumente benutzte. Hilbert fragte daher nach einem strengen, algebraischen Beweis für die Behauptungen der Schubert‘schen Theorie.
 Hermann Schubert, (* 22. Mai 1848 in Potsdam; † 20. Juli 1911 in Hamburg)
Hermann Schubert, (* 22. Mai 1848 in Potsdam; † 20. Juli 1911 in Hamburg)
Mit der Weiterentwicklung der algebraischen Geometrie im 20. Jahrhundert entstanden nach und nach mathematische Hilfsmittel wie die Kohomologietheorie und die Theorie der Multiplizitäten von Grothendieck und Samuel zur Verfügung, mit denen Hermann Schuberts Arbeit formalisiert werden konnte. Auch heute noch ist der Schubert-Kalkül, wenn auch, bezogen auf die ursprünglichen Fragen, in deutlich veränderter und abstrahierter Form, Forschungsgegenstand, bei dem noch nicht alle Fragen restlos geklärt sind.
Problem 16: Was kann über die gegenseitige Lage algebraischer Kurven gesagt werden?
Antwort: Es konnten verschiedene Ergebnisse erzielt werden, viele Fragen bleiben aber offen.
Hilberts sechzehntes Problem fragt nach der Anzahl der Teile und ihrer gegenseitigen Lage von reellen algebraischen Kurven, also Kurven, die von reellen Polynomen erzeugt werden. Die einfachsten Beispiele für algebraische Kurven sind Geraden (beschrieben durch Gleichungen der Form \(ax+by=c\)), Geraden (\(ay-x^2=0\)) und Kreise (x^2+y^2=r^2). Teile meint in diesem Kontext die Zusammenhangskomponenten einer Kurve,: beispielsweise besteht die Kurve \(y^2=x^3-2x\) aus zwei Teilen, einem geschlossenen Oval und einer Kurve, deren Enden (im Falle einer projektiven Ebene) im Unendlichen zusammenlaufen.
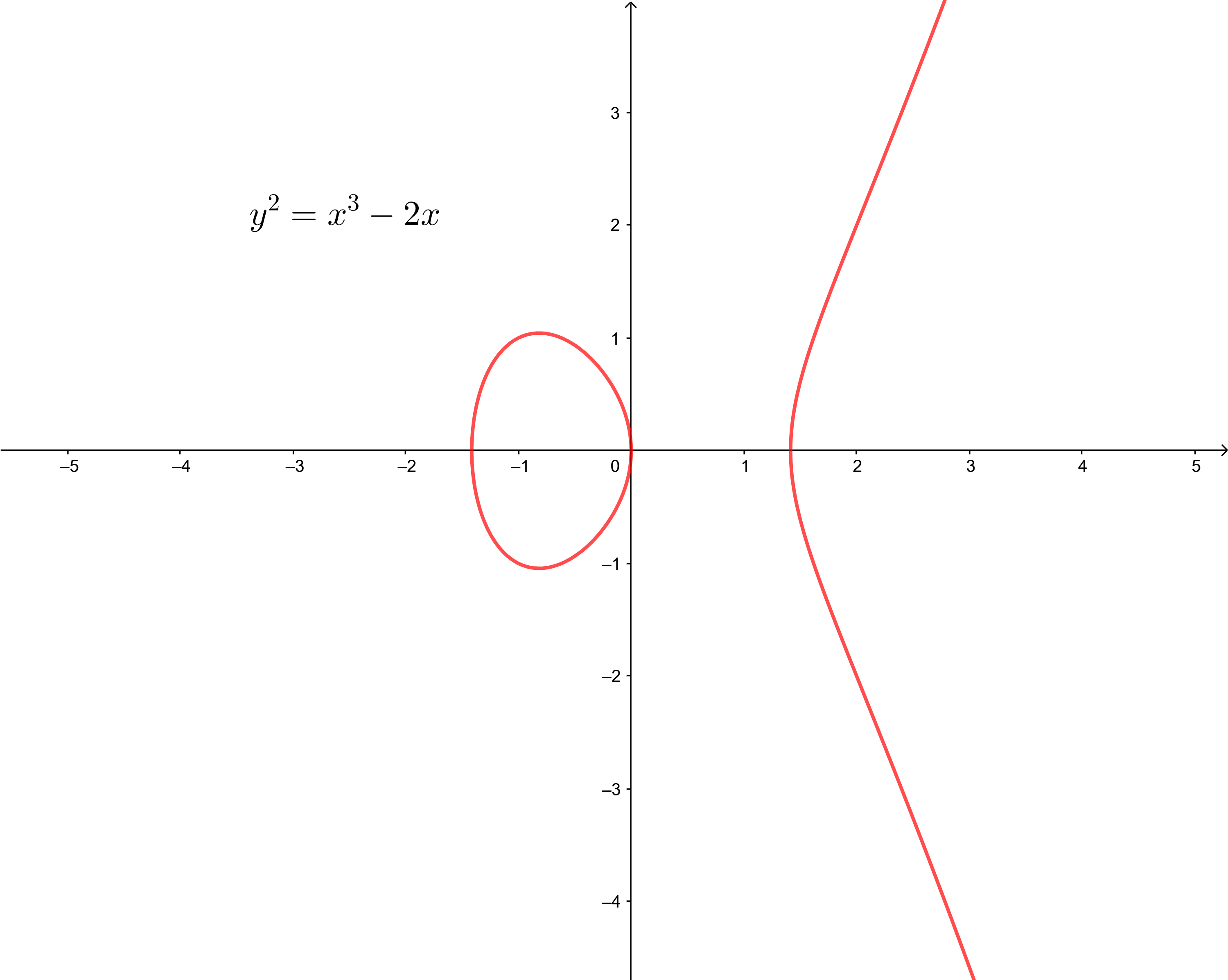 Die Menge aller Punkte (x,y) mit \(y^2=x^3-2x\). sie besteht aus zwei Teilen. Kurven wie diese heißen elliptische Kurven (elliptische Kurven haben mit den namensgebenden Ellipsen nicht (mehr) sehr viel gemein) und spielen in vielen Bereichen der modernen Mathematik, wie der arithmetischen Geometrie, der komplexen Analysis und der Kryptographie eine herausragende Rolle.
Die Menge aller Punkte (x,y) mit \(y^2=x^3-2x\). sie besteht aus zwei Teilen. Kurven wie diese heißen elliptische Kurven (elliptische Kurven haben mit den namensgebenden Ellipsen nicht (mehr) sehr viel gemein) und spielen in vielen Bereichen der modernen Mathematik, wie der arithmetischen Geometrie, der komplexen Analysis und der Kryptographie eine herausragende Rolle.
1876 hat Harnack in einem vielzitierten Aufsatz bewiesen, dass eine algebraische Kurve in der reellen projektiven Ebene aus höchstens \(\frac{n^2-3n+4}{2}\) Teilen besteht und zeigte auch, dass diese Abschätzung scharf ist, indem er sogenannte M-Kurven konstruierte, die über genau diese Anzahl an Teilen verfügen. Als Hilbert sich später selber mit M-Kurven 6. Grades und ihren 11 Teilen beschäftige, fiel ihm auf, dass die Teile nicht beliebig in der Ebene verteilt werden konnten, sondern stets auf bestimmte Weise in einander einbeschrieben waren.
 Die drei möglichen Konfigurationen der maximal möglichen elf Teile algebraischer Kurven sechsten Grades. Die oberste hatte Harnack gefunden, die untere fand Hilbert. Jahrzehnte später bewies Gudkov, dass es auch noch eine dritte mögliche Konfiguration gibt, die mittlere. Er bewies auch, dass es keine andere Konfiguration geben kann. Beachte, dass dies nur schematische Darstellungen sind: insbesondere sind die Teile in Wirklichkeit weder Kreise oder Ellipsen, noch sind sie geradlinig angeordnet.
Die drei möglichen Konfigurationen der maximal möglichen elf Teile algebraischer Kurven sechsten Grades. Die oberste hatte Harnack gefunden, die untere fand Hilbert. Jahrzehnte später bewies Gudkov, dass es auch noch eine dritte mögliche Konfiguration gibt, die mittlere. Er bewies auch, dass es keine andere Konfiguration geben kann. Beachte, dass dies nur schematische Darstellungen sind: insbesondere sind die Teile in Wirklichkeit weder Kreise oder Ellipsen, noch sind sie geradlinig angeordnet.
Er forderte mit seinem sechzehnten Problem, die Struktur dieser gegenseitigen Lage zu untersuchen. Seit den 1930er Jahren beschäftigten sich unter anderen die Russen Iwan Georgijewitsch Petrowski und Olga Oleinik mit dem Problem, die 1948 einen Zusammenhang zwischen M-Kurven und der Eulercharakteristik, einer Invarianten in der kombinatorischen und algebraischen Topologie aufzeigten. Mit der Zeit entstand in der Sowjetunion eine ganze Schule, die an dem Problem arbeitete, der unter anderem D. A. Gudkov, V. M. Kharlamov, Wladimir Arnold und Wladimir Abramowitsch Rochlin angehörten, und die viele wichtige Teilresultate erzielten. Erst in den siebziger Jahren konnte das Problem aber in Gänze gelöst werden.
 Axel Harnack (* 25. April / 7. Mai 1851 Dorpat; † 3. April 1888 in Dresden)
Axel Harnack (* 25. April / 7. Mai 1851 Dorpat; † 3. April 1888 in Dresden)
Problem 17: Kann jede rationale Funktion, die überall dort, wo sie definiert ist, nichtnegative Werte annimmt, immer als Summe von Quadraten dargestellt werden?
Antwort: Ja.
In Ringen und Körpern (Also Mengen, auf denen in sinnvoller Weise Addition, Subtraktion, und, im Falle von Körpern, Division definiert sind), in denen die Begriffe positiv und negativ definiert sind, in dem Sinne, dass unter anderem Summen und Produkte positive Elemente wieder positiv sind, sind Quadratsummen, also Elemente der Form \(x_1^2+...x_n^2\) von besonderem Interesse: Da in solchen Mengen Quadratsummen immer nichtnegativ sind (man denke an ganze oder rationale Zahlen), stellt sich die Frage, ob sich umgekehrt auch jedes nichtnegative Element als Summe von Quadraten schreiben lässt. Dies ist sowohl für die reellen, als auch für die rationalen Zahlen richtig, für reelle Zahlen offensichtlich, bei den rationalen Zahlen folgt das aus dem Lagrange'schen Vier-Quadrate-Satz). Betrachtet man reelle Polynome in \(n\) Variablen (die dann als positiv definiert sind, wenn jedes ihrer Werte positiv, bzw. nichtnegativ, wenn jedes ihrer Werte nichtnegativ ist), stellt man fest, dass es durchaus nichtnegative Polynome geben kann, die nicht die Summe von quadratischen Polynomen sind; das prominenteste Beispiel ist das Motzkin-Polynom \(p(X,Y)=X^4Y^2 + X^2Y^4 − 3X^2Y^2 + 1\), das zwar überall nichtnegative Werte annimmt, aber nicht die Summe von Quadraten von anderen Polynomen ist.
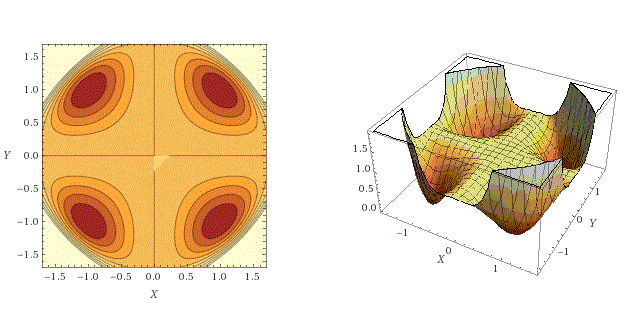 Das Motzkin-Polynom \( p(X,Y)=X^4Y^2 + X^2Y^4 − 3X^2Y^2 + 1\) ist zwar überall nichtnegativ, lässt allerdings nicht als Summe von Quadraten von Polynomen schreiben.
Das Motzkin-Polynom \( p(X,Y)=X^4Y^2 + X^2Y^4 − 3X^2Y^2 + 1\) ist zwar überall nichtnegativ, lässt allerdings nicht als Summe von Quadraten von Polynomen schreiben.
Dass solche Beispiele schwer zu finden sind, zeigt sich daran, dass Hilbert zwar bereits 1888 gezeigt hat, dass solche Polynome existieren müssen, Motzkin sein Beispiel aber erst 1967, also gut 80 Jahre später, vorgestellt hat. Beschränkt man sich hingegen auf rationale Funktionen, also Quotienten von Polynomen, so vermutete Hilbert, sei die Aussage korrekt: Jede rationale Funktion ließe sich als Summe von Quadraten rationaler Funktionen schreiben.
 Graph einer rationalen Funktion (in einer Variablen), der nie unterhalb der x-Achse verläuft. Hilbert vermutete, dass dann die Funktion sich als Summe von Quadraten von rationalen Funktionen schreiben lässt.
Graph einer rationalen Funktion (in einer Variablen), der nie unterhalb der x-Achse verläuft. Hilbert vermutete, dass dann die Funktion sich als Summe von Quadraten von rationalen Funktionen schreiben lässt.
Bewiesen wurde die Aussage 1927 von Emil Artin, mit Hilfe seiner Theorie der reell abgeschlossenen Körper, für die die reellen Zalen den Archetyp darstellen. Hilberts 17. Problem lässt sich auf vielfältige Weise verallgemeinern und spezifizieren, beispielsweise, indem man statt reell abgeschlossener Körper die Teilklasse der geordneten Körper betrachtet (Dubois, 1967) oder nach der kleinstmöglichen Anzahl \(v(d,n)\) rationaler Funktionen fragt, die man benötigt, um ein gegebenes Polynom \(d-\)ten Grades in \(n\) Variablen darzustellen. Pfister zeigte (ebenfalls 1967), dass \(v(d,n) <2^n\) ist; ob es eine bessere Schranke gibt, ist bis heute offen.
Problem 18: Gibt es für jede Dimension nur endlich verschiedene Raumgruppen?
Antwort: Ja.
Hilberts 18. Problem lässt sich der damals noch jungen Disziplin der diskreten Geometrie zuordnen, spezieller der der Kristallographie. In der diskreten Mathematik werden Objekte untersucht, deren geometrische Beschaffenheit durch einzelne, voneinander getrennte Entitäten gegeben sind, wie zum Beispiel Polyeder oder Symmetrieoperationen in Gittern. Raumgruppen sind bestimmte Symmetrieoperationen kristalliner Muster. Unter kristallinen Mustern versteht man Teilmengen des Euklidischen Anschauungsraums, die sich in alle Richtungen des Raums periodisch wiederholen, wie zum Beispiel die Gitter namensgebender Kristalle oder die Menge der ganzen Zahlen als Teilmenge der reellen Zahlen. Kristalline Muster können eine Vielzahl von Symmetrien aufweisen, wie etwa Spiegelsymmetrien, Punktsymmetrien oder diverse Drehsymmetrien. Die Raumgruppe eines kristallinen Musters ist dabei die Menge aller Symmetrieoperationen des kristallinen Musters, die keine Translationen sind. Es war lange bekannt (wurde allerdings erst im späten 19. Jahrhundert bewiesen), dass es nur 17 verschiedene Raumgruppen des zweidimensionalen Raums gibt, drei von ihnen sind in der Abbildung zu sehen. Die oftmals aufgestellte Behauptung, in den Mustern des maurischen Architektur-Meisterwerks Alhambra in Granada finde man alle 17 zweidimensionalen Raumgruppen, ist allerdings unter Wissenschaftler_innen umstritten.
 Die zweidimensionalen Raumgruppen \(P_3\), \(CM\) und \(P_6\) findet man in Ornamenten in der Alhambra. Ob es alle 17 möglichen Raumgruppen dort zu finden gibt, wird kontrovers diskutiert.
Die zweidimensionalen Raumgruppen \(P_3\), \(CM\) und \(P_6\) findet man in Ornamenten in der Alhambra. Ob es alle 17 möglichen Raumgruppen dort zu finden gibt, wird kontrovers diskutiert.
Für den dreidimensionalen Raum befassten sich vor allem die Deutschen Leonhard Sohncke und Arthur Schönfließ, sowie der russische Kristallograf Evgraf Fedorov mit der Klassifizierung der 230 Raumgruppen des dreidimensionalen Raums. Eine systematisierte und vollständige Beschreibung lieferte der englische Amateur-Kristallograf William Barlow 1897.
 Die Kristallstruktur von Diamant (charakteristisch die tetraederförmige Anordnung der Kohlenstoffatome). Nach heutiger Zählung ist die Symmetriegruppe des Diamanten die Gruppe 227 von 230.
Die Kristallstruktur von Diamant (charakteristisch die tetraederförmige Anordnung der Kohlenstoffatome). Nach heutiger Zählung ist die Symmetriegruppe des Diamanten die Gruppe 227 von 230.
Die endliche Anzahl möglicher Raumgruppen für zwei und drei Dimensionen ließ vermuten, dass es auch in höheren Dimensionen nur endlich viele wesentlich verschiedene Raumgruppen gibt. Die Vermutung wurde 1910 von Ludwig Bieberbach gelöst.
 Ludwig Bieberbach (* 4. Dezember 1886 in Goddelau bei Darmstadt; † 1. September 1982 in Oberaudorf in Oberbayern)
Ludwig Bieberbach (* 4. Dezember 1886 in Goddelau bei Darmstadt; † 1. September 1982 in Oberaudorf in Oberbayern)
Später wurde Ludwig Bieberbach Akteur im dunkelsten Kapitel der Geschichte der Mathematik in Deutschland. Bieberbach, SS-Mitglied und glühender Nationalsozialist, war als langjähriger Dekan der Berliner Universität treibende Kraft in der Denunzierung und Verfolgung jüdischer Mathematiker wie Edmund Landau und Issai Schur, mit dem er noch 1928 eine gemeinsame Arbeit veröffentlichte. Er propagierte eine "deutsche Mathematik", die sich gegen den von ihm als "jüdische Mathematik" verstanden Abstraktionsprozess der modernen Mathematik mit Logik, Mengenlehre und der abstrakten Algebra (etwa gegen Cantor und Noether) richtete. Nach der Emigration, Berufsverboten und Suiziden bedeutender jüdischer und nichtjüdischer Mathematiker in Deutschland wie Felix Hausdorff, Emmy Noether, Emil Artin, Issai Schur, Edmund Landau, John von Neumann und Hermann Weyl im Rahmen der nationalsozialistischen „Säuberungspolitik“ verloren Göttingen und Berlin rasch ihren Status als Weltzentren der Mathematik.
Problem 19: Sind alle Lösungen von regulären Variationsproblemen analytisch?
Antwort: Unter gewissen Voraussetzungen, ja.
In der Entwicklung der von Newton angestoßenen Mathematisierung der Physik nahm die Theorie der Differentialgleichungen eine herausragende Stellung ein. Differentialgleichungen sind Gleichungen, bei denen Funktionen gesucht werden, die durch ihre zeitlichen (oder im Falle partieller Differentialgleichungen zeitlichen und örtlichen) Änderungen beschrieben werden. Aus der Newtonschen Mechanik folgt zum Beispiel, dass in einem Federpendel (im Graviations- und reibungsfreien Fall) die Beschleunigung, also die zweite Ableitung der Auslenkung des Pendels, proportional zur Auslenkung des Pendels selbst ist. Dies führt zur Differentialgleichung \[kx +\ddot{x}=0,\] deren Lösungen Funktionen der Form \[A\cos(\sqrt{k}t)+B\sin(\sqrt{k}t),\]
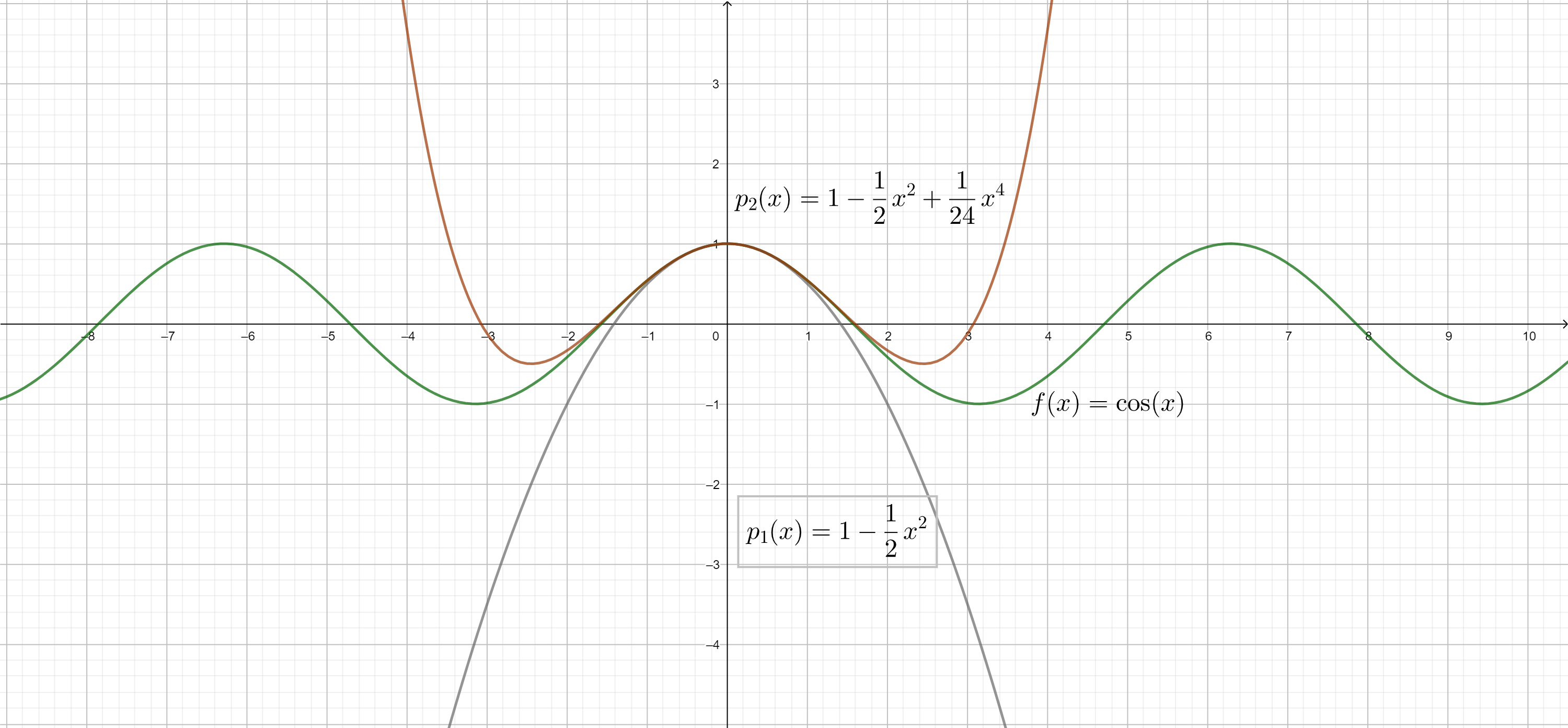 Die Kosinusfunktion lässt sich, wie jede glatte Funktion, durch Polynome mit beliebig hohen Graden annähern. Dass die Funktion allerdings selber als Potenzreihe (sozusagen als Polynom unendlichen Grades) dargestellt werden kann, ist eine besondere Eigenschaft, die nicht auf alle glatten Funktionen zutrifft. Solche Funktionen heißen analytisch.
Die Kosinusfunktion lässt sich, wie jede glatte Funktion, durch Polynome mit beliebig hohen Graden annähern. Dass die Funktion allerdings selber als Potenzreihe (sozusagen als Polynom unendlichen Grades) dargestellt werden kann, ist eine besondere Eigenschaft, die nicht auf alle glatten Funktionen zutrifft. Solche Funktionen heißen analytisch.
also Sinus-Schwingungen sind. Theoretische Physiker und Mathematiker, die sich mit physikalischen Fragestellungen beschäftigten, konnten auf diese Weise zahlreiche Phänomene der klassischen Mechanik, Elektrodynamik und Thermodynamik mathematisch beschreiben. Hilbert bemerkte, dass die Lösungen von (partiellen) Differentialgleichungen in vielen Fällen nicht nur glatt, sondern in einem gewissen Sinne "sehr" glatt waren, nämlich analytisch. Analytisch heißen Funktionen, die sich, zumindest in einer Umgebung eines Punktes, wie Potenzreihen, also wie Funktionen der Form \[f(x)=a_0+a_1 x+a_2x^2+a_3x^3+\dots\] verhalten. Die Exponentialfunktion, Sinus und Kosinus, der Logarithmus, Polynomfunktionen und Wurzelfunktionen (da, wo sie definiert sind) sind alle analytisch, während Funktionen wie die Betragsfunktion (da sie an der Stelle x=0 nicht differenzierbar ist) oder die Funktion \(f(x)= e^{-\frac{1}{x^2}}\) (da sie an der Stelle x=0 schneller gegen Null strebt als jede analytische Funktion, die nicht die Nullfunktion ist) keine analytischen Funktionen sind. Partielle Differentialgleichungen, die von besonderem Interesse für Hilbert waren, waren dabei die in der Variationsrechnung vorkommenden Lagrange-Gleichungen, da er viele Differentialgleichungen, die nur analytische Lösungen zuließen, auf Lagrange-Gleichungen mit gewissen Regularitätsbedingungen zurückführen konnte.
 Sergei Bernstein (* 22. Februar/ 5. März 1880 in Odessa; † 26. Oktober 1968 in Moskau)
Sergei Bernstein (* 22. Februar/ 5. März 1880 in Odessa; † 26. Oktober 1968 in Moskau)
Einen ersten Schritt in Richtung Lösung der ging der russische Mathematiker Sergei Bernstein in seiner Dissertation 1903, indem er die Aussage für den Fall mindestens dreimal differenzierbarer Funktionen bewies. Später konnten unter anderem Leon Lichtenstein, Eberhard Hopf, Ivan Petrovsky und Charles Morrey das Ergebnis verallgemeinern. Eine vollständige Lösung lieferten dann Ennio de Giorgi und John Forbes Nash in den 1950er Jahren.
 Ennio De Giorgio (* 8. Februar 1928 in Lecce; † 25. Oktober 1996 in Pisa)
Ennio De Giorgio (* 8. Februar 1928 in Lecce; † 25. Oktober 1996 in Pisa)
Problem 20: Unter welchen Bedingungen besitzen Randwertprobleme Lösungen?
Antwort: Die Existenz einer Lösung kann nicht in jedem Fall durch eine Beschränkung der Randwerte gesichert werden.
Das 20. Problem in Hilberts Liste ist eng verwandt mit dem 19. und fragt nach Bedingungen, unter denen Randwertprobleme Lösungen besitzen. Randwertprobleme sind typische Problemstellungen in der Theorie der (partiellen) Differentialgleichungen. Ist eine Differentialgleichung gegeben, also eine Gleichung, bei der eine differenzierbare Funktion gesucht ist, deren Ableitungen bestimmte Bedingungen erfüllen müssen, so hat sie im Allgemeinen unendlich viele verschiedene Lösungen; die Gleichung \(\dot{x}=x\) hat zum Beispiel die Lösungen der Form \(x(t)=\lambda e^t\), wobei \(\lambda\) jede beliebige Zahl durchlaufen kann.
 Die Funktionen \(f(x)=\lambda e^x für \lambda=1,2,3,4\). Offenbar erfüllt nur die Funktion \(f(x)=3e^x\) die Anfangsbedingung \(f(0)=3\)
Die Funktionen \(f(x)=\lambda e^x für \lambda=1,2,3,4\). Offenbar erfüllt nur die Funktion \(f(x)=3e^x\) die Anfangsbedingung \(f(0)=3\)
Bei Randwertproblemen wird nun neben dem Erfüllen einer Differentialgleichung auch noch verlangt, dass die Funktion am Rand des untersuchten Gebietes feste, vorgegebene Werte annimmt. Ein Beispiel hierfür ist die Forderung, dass zusätzlich zur oberen Differentialgleichung auch noch \(x(0)=3\) gelten muss; eine Forderung, die offenbar nur die Funkton \(x(t)=3e^t\) erfüllen kann. Aus physikalischer Perspektive werden mit Randwertproblemen physikalische Systeme beschrieben: Die Differentialgleichung beschreibt dabei, wie sich das System verhält, während die Randbedingung die Startkonfiguration festlegt. Ein wichtiger Teilbereich der Theorie der Randwertprobleme ist die Potentialtheorie, bei der gewissen Vektorfeldern sog. Potentiale zugeordnet werden, die man sich als Stammfunktionen differenzierbarer Vektorfelder vorstellen kann. Die Potentialtheorie ist innerhalb der mathematischen Physik aus mehreren Gründen von Bedeutung: Einerseits lassen sich viele Größen in Potentialfeldern leicht berechnen, bspw. können die sonst oft schwer zu berechnenden Wegintegrale, falls ein gegebenes Vektorfeld ein Potential hat, durch Differenzen von Potentialen berechnet werden; andererseits lassen sich viele physikalische Prozesse, darunter die beiden einzigen damals bekannten Wechselwirkungen, die elektromagnetische Wechselwirkung und die Gravitation, durch die Laplace-Gleichung (im Vakuum) und die Poisson-Gleichung (nicht im Vakuum) im Rahmen der Potentialtheorie beschreiben.
 Das Feld \((F_1(x,y),F_2(x,y))=(y^2-x^2,2xy)\). Es ist ein Potentialfeld (das Potential ist durch die roten Linien dargestellt): Das Potential hat dabei die Eigenschaften, dass seine Höhenlinien senkrecht auf den Vektoren des Vektorfeldes stehen und die Länge der Vektoren proportional zum Anstieg des Potentials ist. Felder, die ein Potential haben, haben besonders schöne Eigenschaften, beispielsweise verschwindet entlang eines jeden geschlossenen Pfades das Arbeitsintegral, das heißt, grob gesprochen, dass sich die Pfeile entlang eines geschlossenen Pfades stets „ausgleichen“.
Das Feld \((F_1(x,y),F_2(x,y))=(y^2-x^2,2xy)\). Es ist ein Potentialfeld (das Potential ist durch die roten Linien dargestellt): Das Potential hat dabei die Eigenschaften, dass seine Höhenlinien senkrecht auf den Vektoren des Vektorfeldes stehen und die Länge der Vektoren proportional zum Anstieg des Potentials ist. Felder, die ein Potential haben, haben besonders schöne Eigenschaften, beispielsweise verschwindet entlang eines jeden geschlossenen Pfades das Arbeitsintegral, das heißt, grob gesprochen, dass sich die Pfeile entlang eines geschlossenen Pfades stets „ausgleichen“.
Für eine Lösung einer Poisson-Gleichung wurde das auf Riemann und Dirichlet zurückgehende Dirichletsche Prinzip verwendet, nach dem die Lösung der Poisson-Gleichung eine bestimmte Größe, die Dirichlet-Energie, minimiert. Das Dirichlet-Prinzip war in der damaligen Fachwelt nicht unumstritten, da insbesondere Weierstraß Lücken in der Formulierung des Prinzips fand und Beispiele lieferte, in denen das Dirichletsche Prinzip nicht gilt.
 Stanislaw Zaremba (* 3. Oktober 1863 in Romanówka; † 23. November 1942 in Krakau)
Stanislaw Zaremba (* 3. Oktober 1863 in Romanówka; † 23. November 1942 in Krakau)
Durch die von Hilbert und dem Polen Stanislaw Zaremba eingeführte direkte Methode konnte das Dirichletsche Prinzip mit Methoden der Variationsrechnung rehabilitiert werden. Hilbert fragte nun, ob dem Dirichletschen Prinzip verwandte Methoden zur Sicherstellung der Existenz von Lösungen von Randwertproblemen auch für andere Randwertprobleme, die nicht aus der Potentialtheorie stammen, wie der Theorie der Minimalflächen oder der Theorie der minimalen Gaußschen Krümmung, existiert. Insbesondere fragte er, welche Bedingungen (wie Glattheit, Stetigkeit, Differenzierbarkeit, etc.) in einem gegebenen Randwertproblem erfüllt sein müssen, damit man mit Sicherheit sagen kann, ob eine Lösung existiert. Das Problem erwies sich als äußerst fruchtbar und es gibt umfangreiche Resultate zum Thema, sodass das Problem als gelöst angesehen werden kann. Die ersten wichtigen Schritte zur Lösung kamen wieder von Sergei Bernstein um 1910, weitere Fortschritte unter anderem von Jean Leray (1939).
 Jean Leray (* 7. November 1906 in Chantenay-sur-Loire (heute Teil von Nantes); † 10. November 1998 in La Baule-Escoublac, Département Loire-Atlantique)
Jean Leray (* 7. November 1906 in Chantenay-sur-Loire (heute Teil von Nantes); † 10. November 1998 in La Baule-Escoublac, Département Loire-Atlantique)
Problem 21: Gibt es stets ein System von Fuchsschen Differentialgleichungen bei gegebenen Singularitäten und gegebener Monodromiegruppe?
Antwort: Nein.
Durch die Arbeiten von Riemann, Cauchy und Weierstraß, später aber auch durch Frobenius, Fuchs, Bessel, Liouville und Picard war die Funktionentheorie, die Analysis komplexer Funktionen, eine der am aktivsten beforschten mathematischen Disziplinen. Funktionen, die im Komplexen (oder auf offenen Teilmengen der komplexen Ebene) differenzierbar sind, haben im Vergleich zu ihren reellen Pendants exotische und ungewöhnliche Eigenschaften. Beispielsweise kann man, wenn man die Werte einer komplexwertigen Funktion beim Durchlaufen einer Schlaufe betrachtet, an einen Punkt gelangen, der einen anderen Funktionswert annimmt, als der Punkt, von dem aus man gestartet ist (In Wirklichkeit ist die Theorie komplizierter, man arbeitet hier mit Riemannschen Flächen und Überlagerungen, aber die Vorstellung, dass ein Punkt nach dem Durchlaufen einer Schlaufe einen "neuen" Funktionswert annimmt, ist oftmals nützlich für das Verständnis komplexwertiger Funktionen).
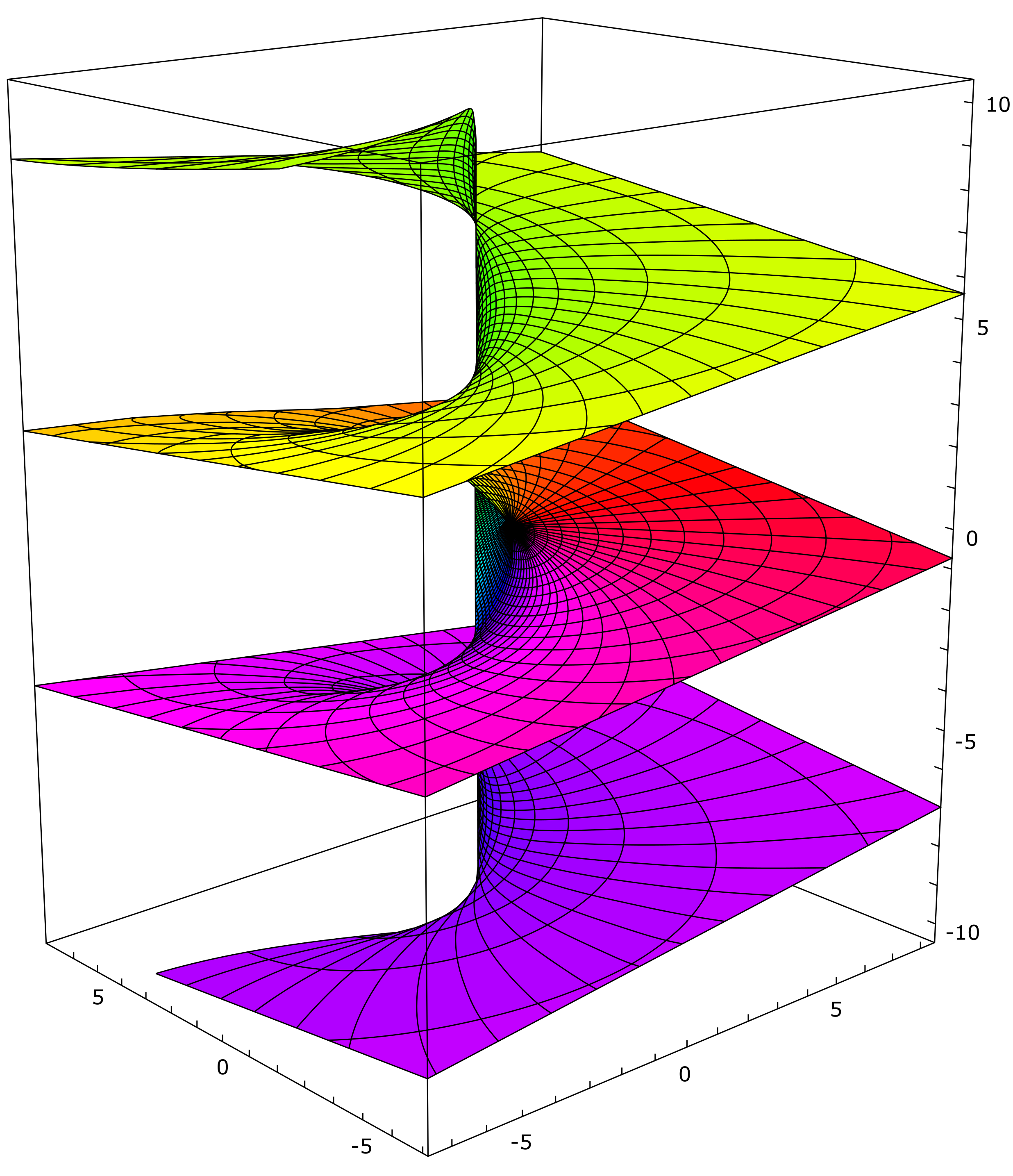 Der Imaginärteil des komplexen Logarithmus. Beschreibt man in der komplexen (horizontalen) Ebene einen Kreis, gelangt man zu einem Funktionswert, dessen Imaginärteil sich um \(2pi\) erhöht hat; Die Monodromiegruppe des komplexen Logarithmus ist daher die Gruppe der ganzen Zahlen.
Der Imaginärteil des komplexen Logarithmus. Beschreibt man in der komplexen (horizontalen) Ebene einen Kreis, gelangt man zu einem Funktionswert, dessen Imaginärteil sich um \(2pi\) erhöht hat; Die Monodromiegruppe des komplexen Logarithmus ist daher die Gruppe der ganzen Zahlen.
Dieses Phänomen wird Monodromie genannt und hat keine Entsprechung in der Theorie der reellwertigen Funktionen; mit einem gewissen Recht sind Monodromien und andere Phänomene, die beim Umlaufen komplexwertiger Funktionen entstehen, der Wesenskern komplexer Funktionen. Die Monodromien wirken auf den Fasern einer Überlagerung; das heißt, dass die Menge der Vertauschungsoperationen, die Punkte durch das Durchlaufen einer Schlaufe erfahren, bilden eine Gruppe, die sogenannte Monodromie-Gruppe. Die Theorie der Differentialgleichungen im Komplexen verfügt ebenfalls über Eigenarten, die der reellen Theorie unbekannt sind. Beispielsweise ist eine Funktion im Komplexen, die mindestens einmal differenzierbar ist, bereits analytisch, das heißt in einer Umgebung eines Punktes \(z_0\) kann sie als Reihe \[f(z)=a_0+a_1(z-z_0)+a_2(z-z_0)^2\dots\] dargestellt werden, was im Reellen grob falsch ist. Ein Fuchssches System (benannt nach Lazarus Fuchs) ist ein homogenes lineares Differentialgleichungssystem \(n\)-ter Ordnung, bei dem die auftretenden Koeffizientenfunktionen Singularitäten von höchstens erster Ordnung haben, das heißt es gibt Punkte, bei denen die Koeffizientenfunktionen nicht definiert sind (solche Punkte heißen Singularitäten), diese sind aber vergleichsweise harmlos (genauer: Eine Singularität \(z_0\) von \(f\) heißt von erster Ordnung, wenn \((z-z_0)f(z)\) analytisch ist, also insbesondere keine Singularität mehr aufweist).
![]() Lazarus Fuchs (* 5. Mai 1833 in Moschin, Provinz Posen; † 26. April 1902 in Berlin)
Lazarus Fuchs (* 5. Mai 1833 in Moschin, Provinz Posen; † 26. April 1902 in Berlin)
Hilberts 21. Problem ist eine Fragestellung aus dem Bereich der komplexen gewöhlichen Dfferentialgleichungen und fragt nach einem Zusammenhang zwischen Fuchsschen Differentialgleichungssystemen und Monodromien. Ihm war bereits bekannt, dass Monodromien bei den Lösungen von Fuchsschen Differentialgleichungssystemen auftauchen. Die Punkte, um die eine Schlaufe durchlaufen wird, sind dabei die Singularitäten der Koeffizientenfunktionen. Hilbert wollte nun den anderen Weg gehen. Gegeben sei eine endliche Menge an Punkten in der komplexen Ebene (tatsächlich wird in der Theorie auf der sog. Riemann-Kugel gearbeitet, bei der man der komplexen Ebene einen als unendlich fern vorgestellten Punkt hinzufügt) und eine Monodromie-Gruppe. Gibt es dann stets ein System von Fuchsschen Differentialgleichungen, dass die gegebene Monodromie-Gruppe und die gegebene Menge der Singularitäten beschreibt? Spezialfälle der Vermutung konnten bereits Poincare und Ludwig Schlesinger im positiven Sinne lösen. 1908 stellte der slowenische Mathematiker Josip Plemelj einen Beweis der Vermutung vor, den die Fachwelt lange Zeit für korrekt gehalten hatte, bis über 80 Jahre später der Russe Andrei Bolibuch eine Lücke in Plemeljs Beweis gefunden hatte und sogar ein Gegenbeispiel konstruieren konnte. Hilberts 21. Problem gilt damit als gelöst: Die Vermutung ist falsch.
Problem 22: Wie können analytische Beziehungen mittels automorpher Funktionen uniformisiert werden?
Antwort: Für Gleichungen mit zwei Variablen gelöst, bei mehr Variablen gibt es noch offene Fragen.
Bei dem Problem der Uniformisierung geht es um die Frage, wie man Mengen (zum Beispiel Teilmengen des zweidimensionalen Anschauungsraums), die durch eine Gleichung mit zwei Variablen definiert sind, mit Hilfe von Funktionen in einer Variablen darstellen kann. Eines der einfachsten Beispiele hierfür ist der Kreis, der sich einerseits beschreiben lässt als die Punkte der Ebene, für die \[x^2+y^2=1\] gilt, andererseits als Menge der Punkte \[\cos(\apha),\sin(\alpha),\] wobei \(\alpha\) alle reellen Zahlen durchläuft. Die Funktion \(f(\alpha)=(\cos(\alpha),\sin(\alpha))\) ist darüber hinaus noch eine periodische Funktion, und damit ein spezielles Beispiel für eine automorphe Funktion, das sind Funktionen, die ihren Wert nicht ändern, wenn eine Gruppe (im obigen Fall die Gruppe der \(2\pi\)-fachen der ganzen Zahlen) auf ihrem Definitionsbereich operiert.
 Die Kosinus- und die Sinusfunktion uniformisieren den Kreis, das heißt, die Menge der Punkte \((x,y)\) mit \(x^2+y^2=1\) lässt sich mit nur einer Variablen \(alpha\) via \((x,y)=(\cos(\alpha),\sin(\alpha)) darstellen. Darüber hinaus sind Sinus und Kosinus periodisch, also in der Sprache von Hilbert automorph.
Die Kosinus- und die Sinusfunktion uniformisieren den Kreis, das heißt, die Menge der Punkte \((x,y)\) mit \(x^2+y^2=1\) lässt sich mit nur einer Variablen \(alpha\) via \((x,y)=(\cos(\alpha),\sin(\alpha)) darstellen. Darüber hinaus sind Sinus und Kosinus periodisch, also in der Sprache von Hilbert automorph.
Poincaré hat bewiesen, dass eine solche Uniformisierung mit Hilfe von automorphen Funktionen stets möglich ist, wenn die Gleichungen, die die gegebene Teilmenge beschreiben algebraische sind, also Polynome in zwei Veränderlichen sind. Hilbert fragte nun, ob eine Uniformisierung durch automorphe Funktionen auch dann noch möglich ist, wenn die Teilmenge durch nichtalgebraische Gleichungen gegeben ist. 1907 konnten Poincaré und unabhängig Paul Koebe das Problem schließlich lösen – allerdings nur für den Fall mit zwei Variablen. Verallgemeinert man das Problem auf mehr als zwei Variablen, so gibt es immer noch ungeklärte Fragen auf diesem Gebiet (Teil eines Programms von William Thurston).
Problem 23: Wie können die Methoden der Variationsrechnung weiterentwickelt werden?
Antwort: Das Problem ist zu vage gestellt, als dass es eine Antwort geben könnte
Bei dem 23. Problem auf Hilberts Liste handelt es sich nicht um eine konkrete Fragestellung, sondern eher um eine Aufforderung die Methoden der Variationsrechnung auszubauen. Die Variationsrechnung beschäftigt sich mit der Suche nach Funktionen, die gewissen Minimalbedingungen genügen. Sie wurde vor allem durch die mathematische Physik inspiriert, da sich in der Elektrodynamik oder der klassischen Mechanik viele Probleme elegant im Rahmen der Variationsrechnung formulieren lassen; die Frage nach der Form einer Kette, die, unter dem Einfluss der Gravitation, an zwei Befestigungen hängt, ist ein Beispiel für ein Problem aus der Variationsrechnung, bei der die sogenannte „Wirkung“ zu minimieren ist.
 Die Frage nach der Kurve, de entsteht, wenn man ein Seil an zwei Punkten anbringt und die Gravitation auf das Seil wirken lässt, ist ein prominentes Beispiel aus der Variationsrechnung. Die Lösung, die sog. Kettenlinie, ist der Graph der Funktion \)\cosh\(, des Hyperbelkosinus. Es gilt \)\cosh(x)=\frac{1}{2}(e^{x}+e^{-x})$
Die Frage nach der Kurve, de entsteht, wenn man ein Seil an zwei Punkten anbringt und die Gravitation auf das Seil wirken lässt, ist ein prominentes Beispiel aus der Variationsrechnung. Die Lösung, die sog. Kettenlinie, ist der Graph der Funktion \)\cosh\(, des Hyperbelkosinus. Es gilt \)\cosh(x)=\frac{1}{2}(e^{x}+e^{-x})$
Bereits Lagrange konnte zeigen, dass sich die gesamte Newtonsche Mechanik im Rahmen dieser Theorie formulieren lässt. Die Funktionalanalysis, die sich in Abgrenzung zur klassischen Analysis mit Räumen von Funktionen und Folgen, statt mit Funktionen und Folgen selbst, beschäftigt und auf Banach, Riesz, Fredholm und nicht zuletzt Hilbert selbst zurückging, lieferte den Rahmen für den Ausbau der Variationsrechnung. Die Variationsrechnung, die sowohl in der Theorie der partiellen Differentialgleichungen, als auch in der Funktionalanalysis aufging, wurde im zwanzigsten Jahrhundert insbesondere durch Stefan Hildebrandt und Guido Stampacchia weiterentwickelt. In heutiger Zeit werden Probleme, die ursprünglich variationstheoretischer Natur waren, oftmals auch mittels Diskretisierung in Probleme der diskreten Optimierung übersetzt – und können so auch mit Computerhilfe gelöst werden.
Problem 24: Wie kann man Kriterien für die Einfachheit eines Beweises aufstellen? In welcher Beziehung stehen zwei verschiedene Beweise des gleichen Satzes zueinander?
Antwort: Die Frage ist zu vage gestellt, aber die Beweistheorie hat immense Fortschritte gemacht und wurde zu einer wichtigen Teildisziplin der mathematischen Logik.
Ein von Hilbert nicht veröffentlichtes, aber für die ursprüngliche Liste vorgesehenes 24. Problem wurde im Jahr 2000 von dem Mathematikhistoriker Rüdiger Thiele von der Universität Leipzig in Hilberts Nachlass entdeckt. Es beschäftigt sich mit Beweistheorie, einem Teilgebiet der mathematischen Logik, bei der mathematische Sätze und vor allem ihre Beweise selbst Gegenstand der Forschung sind. Die Disziplin der Beweistheorie wie auch viele andere Bereiche der Logik existierten zu Hilberts Zeiten noch nicht. Das 24. Problem ist daher auch nicht in einem Strengen logischen Kalkül formuliert, sondern fragt in Alltagssprache nach Kriterien, anhand derer man entscheiden könne, ob ein Beweis unter allen möglichen Beweisen einer Aussage der einfachste sei. Insbesondere fragt Hilbert nach dem Verhältnis zweier Beweise der gleichen Aussage zueinander, und forderte, dass „[…]wenn man 2 Wege hat, […] man nicht bloß diese Wege gehen oder neue suchen, sondern dann das ganze zwischen den beiden Wegen liegende Gebiet erforschen [muss]“, Weiter führte er aus, dass es bei elementargeometrischen Sätzen wie dem Satz des Pythagoras durchaus möglich sei, zu entscheiden, welcher Beweis (von denen es mehr als 100 Stück gibt!) der einfachste sei, da, so Hilbert, ein Beweis einer elementargeometrischen Aussage auf eine algebraische Argumentation zurückzuführen sei, deren Komplexität durchaus messbar und mathematisch fassbar sei.
 Schematische Darstellung von Hilberts 24. Problem
Schematische Darstellung von Hilberts 24. Problem
Vor allem Gödel und Gentzen, aber auch Hilbert selber, setzten sich in den dreißiger Jahren intensiv mit Beweistheorie auseinander und formulierten, teils unabhängig voneinander, Kalküle, in denen sich mathematische Beweise formal untersuchen ließen; Gödels vielzitierter Unvollständigkeitssatz ist Teil dieser Theorie. Ein anderer Themenkomplex dieser Art ist die Frage nach sog. „elementaren“ Beweisen in der Zahlentheorie (wobei „elementar“ hier keinesfalls „einfach“ bedeuten soll). Viele Beweise in der Zahlentheorie nutzen Methoden der komplexen Analysis, und stützen sich dabei auf komplizierte unendliche Reihen, komplexe Integrale, und schwer zu handhabende komplexe Funktionen, wie die Gamma- oder die Zeta-Funktion, obwohl zahlentheoretische Probleme oftmals äußerst leicht zu formulieren sind (zum Beispiel „Ist eine gerade Zahl stets die Summe zweier Primzahlen?“). Es ist daher von Interesse, ob eine wahre, bewiesene zahlentheoretische Aussage, die bisher nur im Rahmen der analytischen Zahlentheorie bewiesen wurde, auch mit „elementaren Methoden“, wie etwa mit Teilbarkeitsargumenten zu beweisen ist. Tatsächlich fanden zum Beispiel 1949 der Fields-Medaillen-Gewinner Atle Selberg und die Mathematiker-Legende Paul Erdös einen elementaren Beweis für den Primzahlsatz, was lange für unmöglich gehalten worden war.
 Paul Erdös (* 26. März 1913 in Budapest, Österreich-Ungarn; † 20. September 1996 in Warschau, Polen)
Paul Erdös (* 26. März 1913 in Budapest, Österreich-Ungarn; † 20. September 1996 in Warschau, Polen)
In der heutigen Beweistheorie sind vor allem sogenannte formale Beweise (engl. formal proofs) von Interesse, das sind Beweise, die derart formalisiert sind, dass spezielle Computerprogramme, sogenannte Proof-Checker, in der Lage sind, sie einzulesen und auf Richtigkeit zu überprüfen. Viele Beweise wurden bereits mit Proof-Checkern überprüft, dazu zählen insbesondere auch solche, bei denen eine Überprüfung durch den Menschen erst gar nicht möglich ist: zum Beispiel kennt der Beweis des Vier-Farben-Satzes nicht weniger als 1400 Fälle, die es jeweils einzeln zu überprüfen gilt; eine Arbeit, die sich bisher noch kein Mensch gemacht hat.


