Der Bonner Professor für theoretische Informatik Norbert Blum hat am 11. August eine Arbeit mit dem Titel: „A Solution of the P versus NP Problem“ veröffentlicht. Die Fachwelt ist in Aufruhr, denn ein solcher Beweis wäre eine Sensation, da das P vs. NP eines der sieben sogenannten Milleniumsprobleme ist. Sie gelten als die derzeit größten ungelösten Herausforderungen der Mathematik.

Aktualisierung vom 4. September 2017: Nachdem Experten in den letzten Wochen eingehend den neuen Beweis für das P vs NP Problem diskutiert haben, ist die allgemeine Meinung, dass er fehlerhaft sei. Blum äußerte sich inziwschen selbst: „Der Beweis ist falsch. Ich muss genau herausfinden, worin der Fehler liegt. Dafür benötige ich etwas Zeit. Ich werde die Erklärung auf meiner Homepage veröffentlichen.“ Die Suche nach einem Beweis für ein weiteres Milleniumsproblem geht also in die nächste Runde...

Auch wenn sich der aktuelle Beweisversuch wohl als nicht richtig erweist, nehmen wir ihn doch gerne zum Anlass, dieses spannende und schwierige mathematische Problem vorzustellen. Denn bislang ist nur eines der Milleniumsprobleme gelöst: Der russische Mathematiker Grigori Perelman bewies im Jahr 2002 die Poincaré-Vermutung.

Das P vs. NP Problem entstammt dem Gebiet der Komplexitätstheorie. Diese ist ein Teilgebiet der theoretischen Informatik und beschäftigt sich mit der Frage, wieviel Rechenaufwand ein Computer zur Lösung eines mathematischen Problems benötigt. Manche Probleme lassen sich relativ schnell lösen, für andere kennt man jedoch keinen geeigneten Algorithmus, und selbst ein Supercomputer bräuchte viele Jahre, um sie zu lösen.

Hintergrund

In der Komplexitätstheorie werden Probleme in Klassen eingeteilt. Die Buchstaben P und NP bezeichnen hierbei verschiedene Klassen. Vereinfacht kann man sagen, dass die „Klasse NP“ Probleme beinhaltet, die leicht aussehen. Als Teilmenge hingegen beinhaltet die „Klasse P“ Probleme, die dann auch tatächlich relativ leicht zu lösen sind. Die berühmte ungelöste Frage des P vs. NP Problems lautet daher in etwa, ob es für alle Probleme, die leicht aussehen auch einen schnellen Lösungsalgorithmus gibt. Schon lange glauben die meisten Informatikerinnen und Informatiker, dass das nicht so ist. Es gäbe demnach "leichte Probleme" der Klasse NP, die sehr viel Rechenzeit benötigen und damit nicht zur Klasse P gehören.

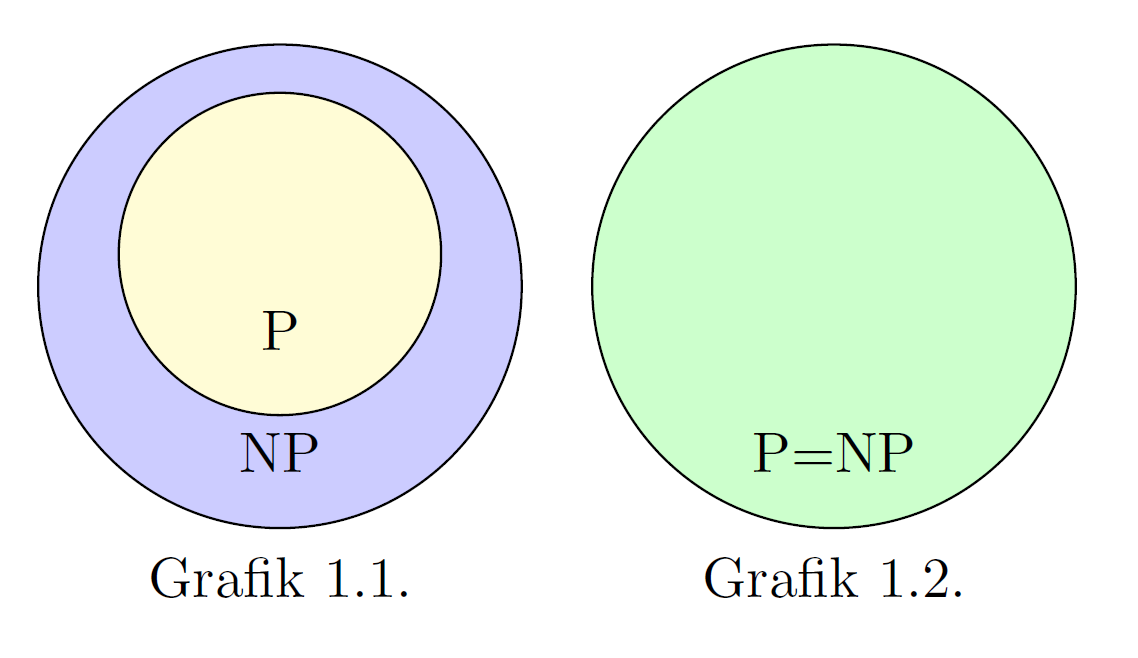
Die Frage des \(P\) vs. \(NP\) Problems lässt sich an den beiden Mengendiagrammen ablesen. Die linke Grafik zeigt den Fall, dass \(P\) eine echte Teilmenge von \(NP\) ist, dass es also Probleme gibt, die in \(NP\) liegen, nicht jedoch in \(P\). Das rechte Diagramm zeigt den Fall, dass \(P\) und \(NP\) dieselbe Mengen sind.

Beispiel "Käse-Maus-Problem"

Ein solches Problem ist das einer Maus, die in einem Labyrinth mehrere Stücke Käse finden soll. Die Maus soll einmal durch das Labyrinth laufen und an jedem Käse einmal abbeißen. An keinem Käse soll sie dabei mehr als einmal vorbeikommen und am Ende zum Ausgang des Labyrinths finden.

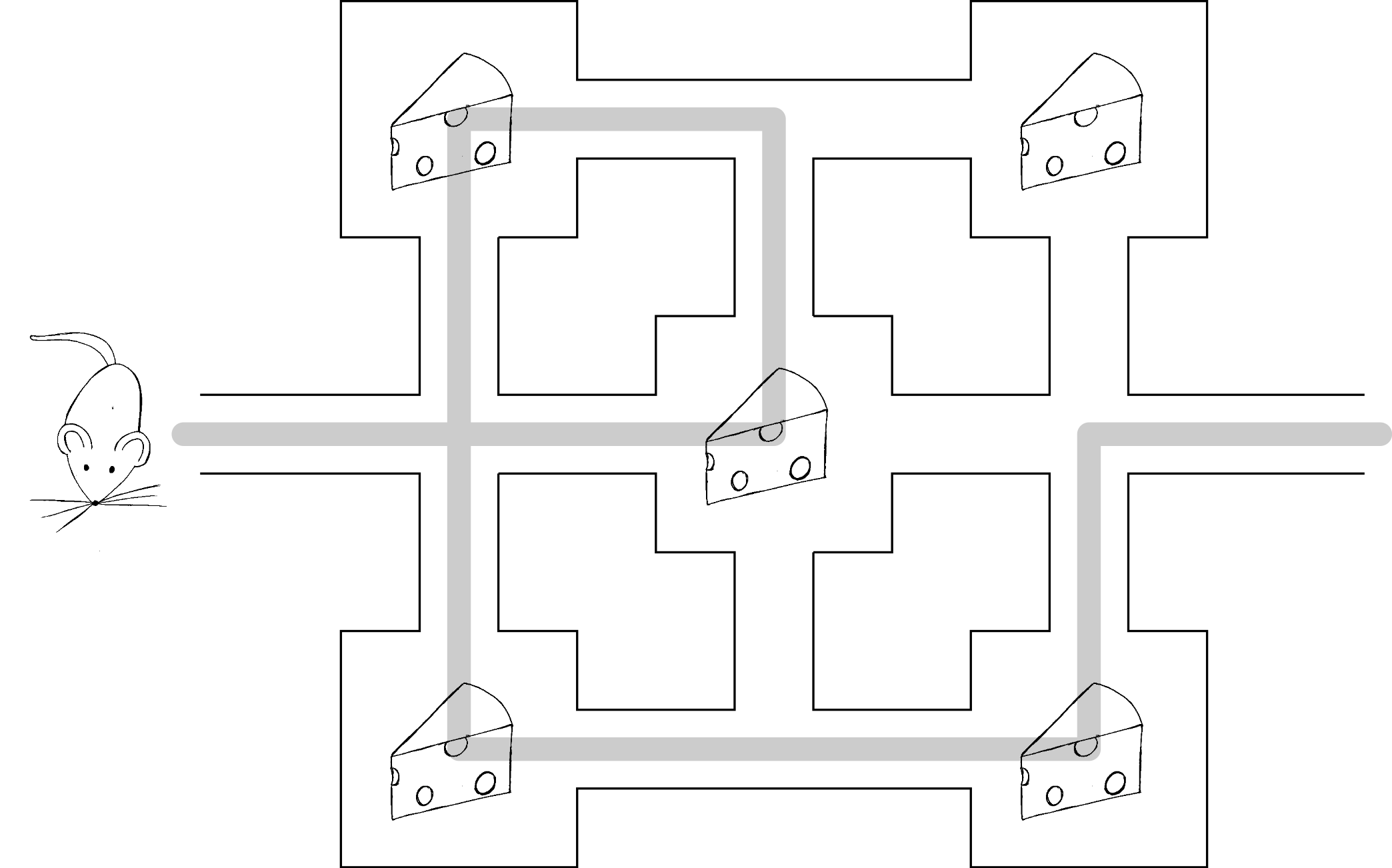
In unserem Beispiel ist die Maus nun entlang der grauen Linie durch das Labyrinth gelaufen. Die graue Linie ist also eine mögliche Lösung. Leicht erkennt man, dass die Maus einen Käse ausgelassen hat. Die graue Linie ist somit keine richtige Lösung für das Problem. Diese Eigenschaft, dass man schnell erkennen kann, ob eine mögliche Lösung richtig oder falsch ist, bezeichnen Wissenschaftlerinnen und Wissenschaftler mit der Abkürzung NP. Das leicht aussehende Maus-Käse-Problem liegt also in der „Klasse NP“.

Wie aber findet die Maus einen geeigneten Weg durch das Labyrinth? Ihr bleibt nicht viel anderes übrig, als es immer wieder zu versuchen. Vielleicht gibt es auch gar keinen Weg. Das kann die Maus aber erst wissen, nachdem sie alle möglichen Wege ausprobiert hat. Das Finden einer Lösung ist demnach viel komplizierter und dauert länger als das Überprüfen eines einzigen möglichen Weges. Das Maus-Käse-Problem, Mathematiker und Mathematikerinnen nennen es das Hamiltonkreisproblem, gehört damit nicht zur „Klasse P“ der relativ schnell lösbaren Probleme.

Auch Informatikerinnen und Informatiker kennen bis dato keine bessere Strategie, als das Ablaufen aller Möglichkeiten. In unserem Beispiel mit fünf Käsestücken lässt sich ein solcher Weg sicherlich irgendwann finden, wenn es ihn gibt. Erhöht man die Anzahl der Käsestücke aber auf 90, so benötigt man bereits ca. hundert Quadrillionen Rechenoperationen, um einen Weg zu bestimmen. Das ist eine Eins mit 26 Nullen. Selbst der derzeit schnellste Computer der Welt, der Sunway TaihuLight aus China, bräuchte hierzu mindestens 100 Jahre!

Die Frage ist also, ob es eine schnellere Methode zur Lösung gibt und man sie einfach noch nicht gefunden hat oder ob es in der Struktur des Problems liegt, dass es einfach nicht schneller zu lösen ist. Das ist das P vs. NP Problem. Der oben genannte Informatikprofessor Blum hat nun einen Beweis vorgelegt, der besagt, dass alle Probleme, die dem Maus-Käse-Problem ähneln, tatsächlich zu komplex sind, um einen schnelleren Algorithmus zu finden.

Ist nun das zweite Milleniumsproblem gelöst?

Ob der vorgelegte Beweis des Bonner Mathematik-Professors Blum der Begutachtung durch seine Kolleginnen und Kollegen standhält, wird sich im Laufe der nächsten Wochen und Monate zeigen. Der Berliner Informatikprofessor Günter Rote sagt dazu: „Ich bin da sehr vorsichtig. Bei der Lösung von solch großen Problemen ist immer gesunde Skepsis angesagt.“

„Norbert Blum ist ein Experte für Komplexitätstheorie und kennt sich hier wirklich gut aus, da er schon lange auf diesem Gebiet arbeitet“, sagt Wolfgang Mulzer, sein Professorenkollege an der Freien Universität Berlin. Er selbst sei eher skeptisch, würde sich aber freuen, wenn der Beweis stimmen sollte. Niemand habe damit gerechnet, noch zu Lebzeiten einen korrekten Beweis des P vs. NP Problems zu Gesicht zu bekommen. Zu groß erscheine die Lücke, die noch zu schließen sei...

Sollte sich der Beweis als gültig herausstellen, wird Norbert Blum nicht nur eine Menge Anerkennung durch die Fachwelt zuteil. Er erhält dann auch eine Million Dollar als Preisgeld, das das Clay Institut in Massachusetts zur Lösung jedes Milleniumsproblems ausgesetzt hat.

 Text und Abbildungen: Anna Maria Hartkopf, Institut für Mathematik, Freie Universität Berlin

Um einen Kommentar zu verfassen, müssen Sie sich einloggen bzw. kurz als Gast registrieren.