Die Geschichte der komplexen Zahlen ist eng verknüpft mit der Geschichte der Lösungsformeln für Polynomialgleichungen, wie beispielsweise quadratische, kubische und quartische Gleichungen. Im 16. Jahrhundert, der Zeit der Renaissance, war das Lösen von Polynomialgleichungen eine der Hauptbeschäftigungen italienscher Mathematiker wie Scipione del Ferro, Niccolo Tartaglia, Raffael Bombelli und Geralomo Cardano. Letzteren ist die Einführung der komplexen Zahlen zu verdanken: Zunächst wurde die imagninäre Einheit nur als Spielerei betrachtet oder bestenfalls als Möglichkeit, nicht vorhandenen Lösungen einen Sinn zukommen zu lassen; dass das Quadrat einer Zahl tatsächlich negativ sein könnte, war in der damaligen Mathematik undenkbar.

Geralomo Cardano (1501-1576)

Nachdem jedoch Bombelli komplexe Zahlen benutzte, um reelle (also nach damaliger Lehrmeinung tatsächlich existierende) Lösungen kubischer Gleichungen zu finden, wurde die Fruchtbarkeit und Tiefe der Theorie klar: die komplexen Zahlen hatten ihre Daseinsberechtigung in der Mathematik gefunden.

Diese Herangehensweise sollte beispielhaft sein für viele Resultate der klassischen Mathematik, egal ob in der Analysis, der Algebra, der Stochastik oder der Geometrie: um ein Problem im Reellen zu lösen, ist es oftmals hilfreich oder notwendig, den „Umweg über das Komplexe“ zu beschreiten. Zahlreiche Beweise von Theoremen, die im Rellen nur schwer zu führen sind, werden mit komplexen Zahlen zu Einzeilern.

Der Begriff der imaginären Zahl wurde 1637 von René Descartes eingeführt. Dieser Ausdruck war der (heute nicht mehr aktuellen) Anschauung geschuldet, nach der es sich bei den imaginären Zahlen nicht um tatsächlich existierende, sondern um "eingebildete", also imaginäre Zahlen handelt. Leibniz griff diese Auffassung auf und ergänzte sie um eine theologische Komponente, indem er die komplexen Zahlen als “eine wunderbare Zuflucht des göttlichen Geistes –beinahe ein[en] Zwitter zwischen Sein und Nicht-Sein” bezeichnete.

René Descartes (1596-1650)

Erst Caspar Wessel (1797) und Rowan William Hamilton (1833) gelang eine formal korrekte Definition der komplexen Zahlen. Spätestens seitdem wurden die komplexen Zahlen von Mathematikerinnen und Mathematikern als genauso „existent“ angesehen wie die reellen Zahlen.

Einen gewaltigen Fortschritt machte die Theorie der komplexen Zahlen im Jahre 1748 durch den Ausnahmemathematiker Leonhard Euler. In seiner Schrift „Introductio in analysin infinitorum“ veröffentlichte er seine berühmte Formel, in der er mit Hilfe der komplexen Zahlen einen Zusammenhang zwischen der Exponentialfunktion und den trigonometrischen Funktionen herstellte – ein Zusammenhang, der ohne die komplexen Zahlen nicht möglich gewesen wäre! Euler erweiterte die Exponentialfunktion um komplexe Argumente und zeigte, dass der Real- und Imaginärteil der komplexen Exponentialfunktion gerade die trigonometrischen Funktionen sind, genauer:

Wegen ihrer Eigenschaft, die trigonometrischen Funktionen durch die wesentlich leichter handzuhabenden Exponentialfunktion zu ersetzen, findet die eulersche Formel auch Anwendung in der Physik: Überall dort, wo in der Physik Wellen und Periodizität auftauchen, also zum Beispiel in der Optik, der Elektrodynamik, oder selbst in der klassischen Mechanik, können die jeweiligen Phänomene mathematisch elegant und prägnant mit Hilfe komplexer Zahlen und der Exponentialfunktion beschrieben werden.

Leonhard Euler (1707-1783)

Ein wichtiger Spezialfall der eulerschen Formel, die eulersche Identiät, gilt unter Mathematikern und Mathematikerinnen allgemein als die schönste Formel der Mathematik: Sie verbindet die fünf wichtigsten Zahlen der Mathematik, \(e\), \(π\), \(i\), \(1\) und \(0\) (und nur die), und die wichtigsten Grundrechenarten der Mathematik, die Addition, die Multiplikation und das Potenzieren (und nur die) in einer einzigen Formel: Setzt man in die obige Formel für \(\varphi\) die Zahl \(\pi\) ein, so ergibt sich \(e^{i\pi}=\mathrm{cos}(\pi)+i\mathrm{sin}(\pi)=-1+i\cdot 0=-1\) oder:

Der Mathematiker und Autor Kevin Devlin sollte später in seinem Buch „Dr. Euler's Fabulous Formula: Cures Many Mathematical Ills“ festhalten: „Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's equation reaches down into the very depths of existence.”

Während Euler die komplexen Zahlen in der (noch jungen) Analysis einführte, beschäftigte sich Gauß darüber hinaus auch mit der Anwendung der komplexen Zahlen in der Geometrie und der Algebra. 1811 führte er seine berühmte Zahlenebene ein, mit der es möglich war, komplexe Zahlen graphisch als Punkte bzw. Vektoren in der Ebene darzustellen. Rechenoperationen komplexer Zahlen lassen sich dadurch als geometrische Operationen auffassen und andersherum- dies macht es möglich, zahlreiche Sätze der Elementargeometrie rechnerisch zu beweisen; insbesondere bildet diese geometrische Interpretation der komplexen Zahlen eine der theoretischen Grundlagen für den Beweis der Unmöglichkeit der Quadratur des Kreises. Mit der Einführung der gaußschen Zahlenebene veränderte sich auch das Verhältnis zur Frage nach der Existenz imaginärer Zahlen: Die Vorstellung der komplexen Zahlen als Punkte in einer Ebene nahmen der imaginären Einheit viel ihres vormals rätselhaften Charakters. Gauß lehnte zum Beispiel den Descartesschen Begriff der imaginären Zahl ab und verwendete stattdessen den weit weniger mysterriös wirkenden Begriff "lateral", was schlicht "seitlich", in Hinblick auf die Zweidimensionalität der komplexen Zahlen, bedeutet; der Begriff konnte sich allerdings nicht durchsetzen.

Carl Friedrich Gauß (1777-1855)

Gauß' bedeutendster Beitrag zur Theorie der komplexen Zahlen war allerdings der Beweis des Fundamentalsatzes der Algebra, eines der wichtigsten Resultate der Algebra und der komplexen Analysis. Nach dem Fundamentalsatz hat ein Polynom \(n\)-ten Grades stets \(n\) Nullstellen (solange man erlaubt, dass zwei, oder mehr Nullstellen auch „zusammenfallen“ können), was im reellen offensichtlich falsch ist. Der Fundamentalsatz der Algebra hat zahlreiche Konsequenzen: Beispielsweise folgt aus ihm, dass jeder Vektorraumendomorphismus Eigenwerte besitzt; dieses Ergebnis spielt in der Operatorentheorie von Hilberträumen, und damit in den mathematischen Grundlagen der Quantenmechanik eine wichtige Rolle.

Die Entwicklung der modernen Analysis durch Riemann, Cauchy und Weierstrass Anfang des 19. Jahrhunderts beflügelte die Theorie der komplexen Zahlen in nicht dagewesener Weise. Riemann und Cauchy gelang es, das Kalkül auf der Integral- und Differentialrechnung aus dem reellen auf die komplexen Zahlen zu übertragen: Dies war die Geburtsstunde der modernen Funktionentheorie, einer Theorie, die heute, 200 Jahre später, in nahezu unveränderter Form an Universitäten gelehrt wird. Wie schon in der Theorie der Polynomialgleichungen war auch in der Analysis der Gebrauch komplexer Zahlen nur selten reiner Selbstzweck, sondern stellte ein mächtiges Werkzeug dar, mit dem man in der Lage war, nicht, oder nur schwerlich lösbare Probleme aus der reellen Analysis auf eine elegante Art lösen zu können.

Bernhard Riemann (1826-1866) und Augustin-Louis Cauchy (1789-1857)

Bei seinen Untersuchungen zu der nach ihm benannten komplexen \(\zeta\)-Funktion stieß Riemann 1859 auf ein Phänomen, welches sich später als eines der hartnäckigsten offenen mathematischen Probleme überhaupt herausstellen sollte: Er erkannte, dass die Nullstellen der Zetafunktion, abgesehen von den negativen geraden Zahlen, den trivialen Nullstellen, allesamt einen Realteil von genau \(\frac{1}{2}\) haben. Bis heute (2018) konnte man weder die Behauptung beweisen, noch konnte sie durch ein Gegenbeispiel widerlegt werden. Das revolutionäre an Riemanns Untersuchungen war die Anwendung seiner Theorie in einem Teilgebiet der Mathematik, welches auf den ersten Blick von der Analysis nicht weiter hätte entfernt sein können: Der Zahlentheorie. In der Tat bildet die Schrift „über die Anzahl der Primzahlen unter einer gegebenen Größe“ den Beginn der analytischen Zahlentheorie, in der Probleme in der Zahlentheorie mit Methoden der komplexen Analysis gelöst werden.

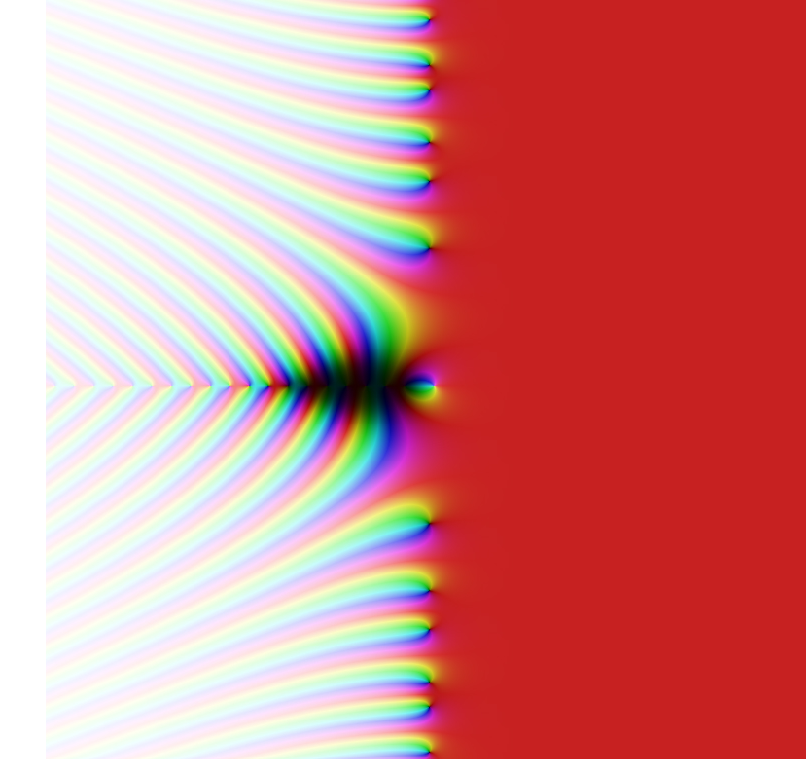Die Riemannsche \(\zeta\)-Funktion in der Gaußschen Zahlenebene. Die schwarzen "Knoten" sind die Nullstellen der Funktion.

Heutzutage werden die komplexen Zahlen wie selbstverständlich in allen Bereichen der Mathematik benutzt; bisweilen geht man in der modernen Mathematik sogar den umgekehrten Weg und benutzt die komplexen Zahlen, um die Zahl \(\pi\) und die trigonometrischen Funktionen überhaupt erst zu definieren: Die Kosinus- und Sinusfunktion ist dann definiert als der Real- bzw. Imaginärteil der komplexen Exponentialfunktion (welche über ihre Reihendarstellung definiert wird), während \(\pi\) definiert ist als das doppelte der kleinsten positiven Nullstelle der Kosinusfunktion. Viele Gebiete, wie zum Beispiel der Großteil der modernen algebraischen Geometrie oder der Theorie der \(C^*\)-Algebren, würden ohne die angenehmen Eigenschaften der komplexen Zahlen gar nicht erst existieren.

Konrad Krug

Um einen Kommentar zu verfassen, müssen Sie sich einloggen bzw. kurz als Gast registrieren.