Die Weihnachtszeit- Das ist die Zeit Besinnlichkeit und der Einkehr, die Zeit von Plätzchen und Lebkuchen, die Zeit für Familie; und natürlich auch die Zeit, die Liebsten mit der einen oder anderen Aufmerksamkeit zu bedenken. Aus diesem Grund erfreut sich das Wichteln seit einiger Zeit einer immer größeren Beliebtheit im Büro, im Klassenzimmer oder im Familienkreis. Beim Wichteln (oder Secret Santa im Englischen) geht es darum, den Kolleg/innen, Mitschüler/innen oder Familienmitgliedern anonym Geschenke zukommen zu lassen. Dabei erhält jede teilnehmende Person zufällig den Namen einer anderen Person, die es zu beschenken gilt; bei der Verlosung der Namen müssen folgende Regeln eingehalten werden:
(a) Jede Person muss genau einmal schenken.
(b) Jede Person muss genau ein Geschenk erhalten.
(c) Man darf nicht seinen eigenen Namen ziehen.
(d) Eine beschenkte Person darf nicht wissen, von wem das Geschenk stammt.
(e) Alle Konstellationen sollen die gleiche Wahrscheinlichkeit haben.
Wir wollen nun verschiedene Methoden zur Namensverteilung angeben, und diese auf nach den oben genannten Kriterien untersuchen. Dabei stellen wir auch eine scheinbar ideale Methode der Mathematikerin Hannah Fry vor, die auf dem Youtube-Kanal Numberphile veröffentlicht wurde und zeigen, dass auch diese Methode nicht von Unzulänglichkeiten befreit ist.
 Die Freunde Ada, Bernhard, Carl, Dorothy, Emmy und Felix wollen sich gegenseitig etwas schenken. Wie gehen sie dabei am besten vor?
Die Freunde Ada, Bernhard, Carl, Dorothy, Emmy und Felix wollen sich gegenseitig etwas schenken. Wie gehen sie dabei am besten vor?
Methode 1: Jede Person zieht reihum, sobald jemand den eigenen Namen zieht, legt diese Person den gezogenen Namen zurück und zieht einen Neuen.
Dies ist die gängigste Methode zur Ermittlung der Zuordnung. Auf den ersten Blick scheint sie alle Kriterien zu erfüllen: Durch das zurücklegen wird auf den ersten Blick verhindert, dass der eigene Name gezogen wird, jede Person schenkt jeder anderen Person und wird auch genau einmal beschenkt. Eine offensichtliche Schwachstelle der Methode ist aber, dass dadurch nicht immer verhindert wird, dass die letzte Person den eigenen Namen zieht. Die zweite, entscheidendere Schwachstelle aber ist, dass die Wahrscheinlichkeit, den Namen einer Person zu ziehen, massiv davon abhängt, an welcher Position man beim Ziehen der Namen sitzt: Regel (e) wird also verletzt. Den Grund dafür zeigt Fry in dem verlinkten Video.
Methode 2: Jede Person zieht reihum, sobald jemand den eigenen Namen zieht, ziehen alle Personen neu.
Mit dieser Methode wird das Problem der Nichtgleichverteilung aus Methode 1 offenbar vermieden. Allerdings ist es so, dass die Wahrscheinlichkeit, den eigenen Namen zu ziehen (Namensverteilungen, bei denen das nicht der Fall ist, werden fixpunktfreie Permutationen oder derangements genannt) stets relativ hoch ist: Sie pendelt sich schnell auf den Wert \(\frac{1}{e} \approx 0,63…\) ein; das heißt in \(63\%\) der Fälle muss das Verfahren wiederholt werden- Dies kann den Wichtelspaß erheblich beeinträchtigen. Ein Beweis dafür befindet sich im Aufklapper unten.
Berechnung der Wahrscheinlichkeit für fixpunktfreie Iterationen
\begin{align*}
!n=\sum_{k=0}^{n} (-1)^k\frac{1}{k!}
\end{align*}
Zunächst muss man sich klarmachen, was \(!1\) und \(!2\) sind: Es gibt bei einer einelementigen Menge nur eine Möglichkeit zur Permutation, und diese hat offenbar einen Fixpunkt (nimmt nur eine Person am Wichteln teil, zieht diese zwangsläufig den eigenen Namen), es gilt also \(!1=0\). Für \(n=2\) gibt es zwei Permutationen, von denen genau eine fixpunktfrei ist: Die beiden Teilnehmer/innnen ziehen jeweils den Namen des/der anderen; es gilt also \(!2=1\).
Wir wollen das Problem nun für ein beliebiges \(n\) lösen. Dafür betrachten wir zunächst eine Gruppe von \(n\) Personen, die mit \(1,2,…,n\) durchnummeriert sind und Zettel, auf denen die Namen der Personen \(1,2,…,n\) stehen. Person \(1\) hat nun \((n-1)\) Möglichkeiten, einen Zettel zu ziehen, auf dem nicht der eigene Name steht. Nehmen wir nun an, Person \(1\) hat den Zettel Nummer \(3\) (oder allgemein: Zettel Nummer \(k\)) gezogen. Nun kann man für die Ziehungen der Person Nummer \(3\) genau zwischen zwei Fällen unterscheiden:
1. Person \(3\) zieht den Namen von Person \(1\). Dann reduziert sich für das Problem auf die Suche nach \(!(n-2)\), da für zwei Personen die jeweilige Zuordnung bereits feststeht.
2. Person \(3\) zieht nicht den Namen von Person \(1\). Dann reduziert sich das Problem auf die Suche nach \(!(n-1)\), da für eine Personen die jeweilige Zuordnung bereits feststeht.
Insgesamt gilt also:
\begin{align*}
!n=(n-1)(!(n-2)+!(n-1)).
\end{align*}
Um nun die obige Formel zu beweisen benutzen wir die Beweismethode der vollständigen Induktion: um eine Aussage für alle natürlichen Zahlen zu beweisen, zeigt man, dass die Aussage für kleine \(n\) gilt, und beweist dann, dass die Aussage auch für den Nachfolger \(n+1\) gilt. Dass die Formel für kleine \(n\) gilt, haben wir oben bewiesen. Wir beginnen mit der Induktion: Wir wollen zeigen, dass für \(n+1\) gilt:
\begin{align*}
!(n+1)=\sum_{k=0}^{n+1}(-1)^k\frac{1}{k!}
\end{align*}
und setzen dabei vorraus, dass die Formel für \(n\) und \(n-1\) bereits stimmt.
Wir rechnen:
\begin{align*}
!(n+1)&=n\cdot (!n+!(n-1)) &&\mid \text{Formel von oben}
\\&=n\cdot!n+n \cdot !(n-1)
\\&=n\cdot\underbrace{ n!\cdot \sum_{k=0}^n (-1)^k\cdot\frac{1}{k!}}_{\text{Induktionsvoraussetzung}}+n\cdot \underbrace{ (n-1)!\cdot \sum_{k=0}^{n-1} (-1)^k\cdot\frac{1}{k!}}_{\text{Induktionsvoraussetzung}}&&\mid n\cdot (n-1)!=n!
\\&=n!\cdot (n\cdot \sum_{k=0}^n (-1)^k\cdot\frac{1}{k!}+\sum_{k=0}^{n-1} (-1)^k\cdot\frac{1}{k!})
\\&=n!\cdot (n\cdot \sum_{k=0}^n (-1)^k\cdot\frac{1}{k!}+\sum_{k=0}^{n-1} (-1)^k\cdot\frac{1}{k!}\underbrace{+(-1)^n\cdot \frac{1}{n!}-(-1)^n\cdot \frac{1}{n!}}_{=0})
\\&=n!\cdot (n\cdot \sum_{k=0}^n (-1)^k\cdot\frac{1}{k!}+\underbrace{\sum_{k=0}^{n-1} (-1)^k\cdot\frac{1}{k!}+(-1)^n\cdot \frac{1}{n!}}_{=\sum_{k=0}^n (-1)^k\cdot\frac{1}{k!}}+(-1)^{n+1}\cdot \frac{1}{n!})
\\&=n!\cdot ((n+1)\cdot \sum_{k=0}^n (-1)^k\cdot\frac{1}{k!}+(-1)^{n+1}\cdot \frac{1}{n!})
\\&=n!\cdot ((n+1)\cdot \sum_{k=0}^n (-1)^k\cdot\frac{1}{k!}+(-1)^{n+1}\cdot \frac{1}{n!}\cdot\frac{n+1}{n+1})
\\&=n!\cdot (n+1)\cdot (\sum_{k=0}^n (-1)^k\cdot\frac{1}{k!}+(-1)^{n+1}\cdot \frac{1}{n!}\cdot\frac{1}{n+1})
\\&=n!\cdot (n+1)\cdot (\underbrace{\sum_{k=0}^n (-1)^k\cdot\frac{1}{k!}+(-1)^{n+1}\cdot \frac{1}{(n+1)!}}_{=\sum_{k=0}^{n+1}(-1)^k\frac{1}{k!}})
\\&=(n+1)!\cdot\sum_{k=0}^{n+1}(-1)^k\frac{1}{k!},
\end{align*}
was zu zeigen war. Da es \(n!\) Permutationen einer Menge mit \(n\) Elementen gibt, ist die Wahrscheinlichkeit für eine fixpunktfreie Permutation
\begin{align*}
\mathbb{P}(\mathrm{fixpunktfrei})= \sum_{k=0}^{n}\frac{1}{k!},
\end{align*}
was wegen der Potenzreihenentwicklung der Exponentialfunktion
\begin{align*}
e^x=\sum_{k=0}^\infty x^k \frac{1}{k!}
\end{align*}
schnell gegen
\begin{align*}
e^{-1}=\frac{1}{e}=0,63…
\end{align*}
konvergiert.
Methode 3: Die Methode von Hannah Fry
Eine wesentlich bessere Möglichkeit, die Namen zu verteilen, stellt die Mathematikerin Hannah Fry im Youtube-Kanal Numberphile vor. Die Quintessenz von Frys Methode ist es, sowohl die Namen der Schenkenden, als auch die Namen der zu beschenkenden per Los zu verteilen. In einem Zwischenschritt wird dann sichergestellt, dass niemand sich selber beschenkt.
Es nehmen zum Beispiel die Freunde Ada, Bernhard, Carl, Dorothy, Emmy und Felix am Wichteln teil, also sechs Personen.
Schritt 1: Zunächst nimmt man sechs Zettel, knickt sie in der Mitte, und schreibt auf den ersten Zettel jeweils über den Knick „du bist Nummer 1“ und unter den Knick „dein Geschenk geht an Nummer 1“. So fährt man fort, bis auf dem letzten Zettel „du bist Nummer 6“, bzw. „dein Geschenk geht an Nummer 6“ steht.
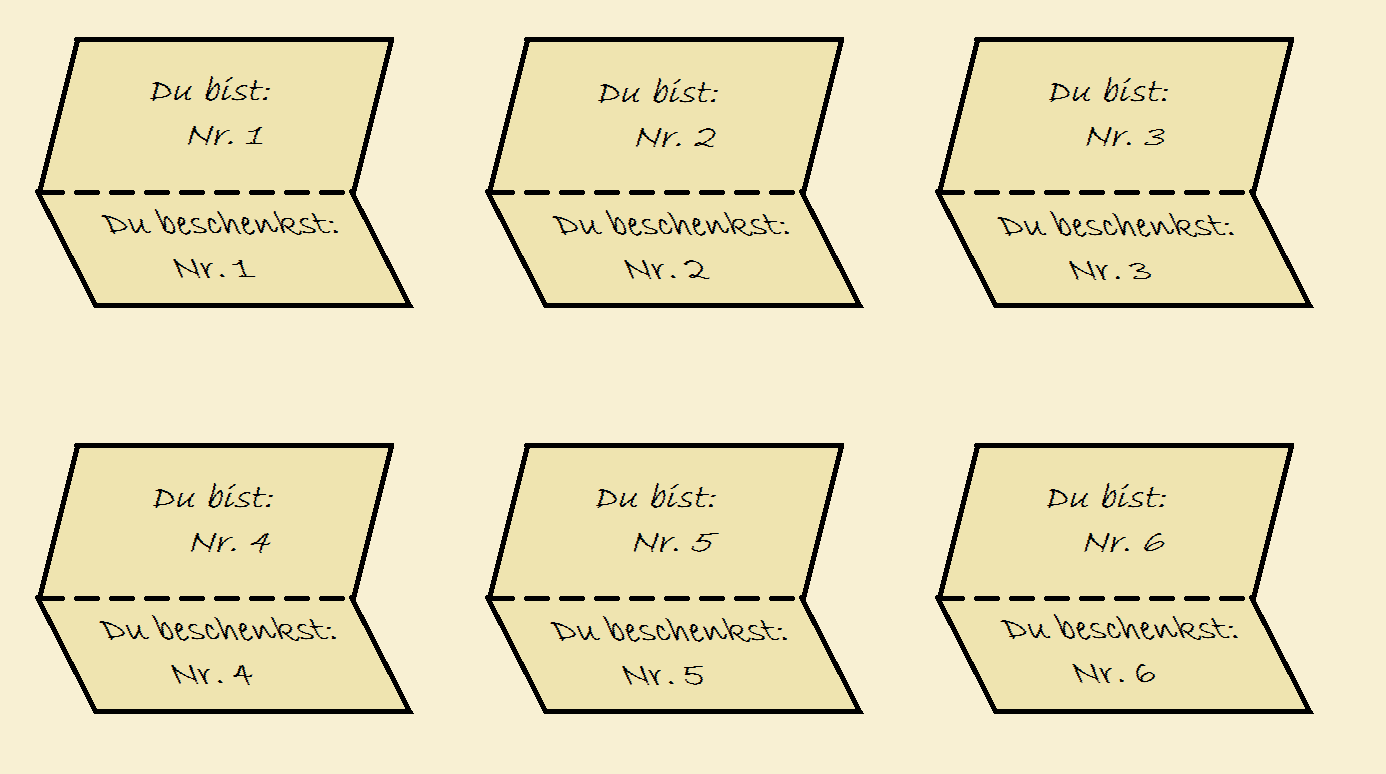
Schritt 2: Anschließend mischt man die Zettel, und schneidet sie in der Mitte durch. Der obere Teil wird nun um eine Position nach rechts verschoben und mit der neuen unteren Hälfte zusammengeklebt; dadurch wird vermieden, dass eine Person sich selbst beschenkt.
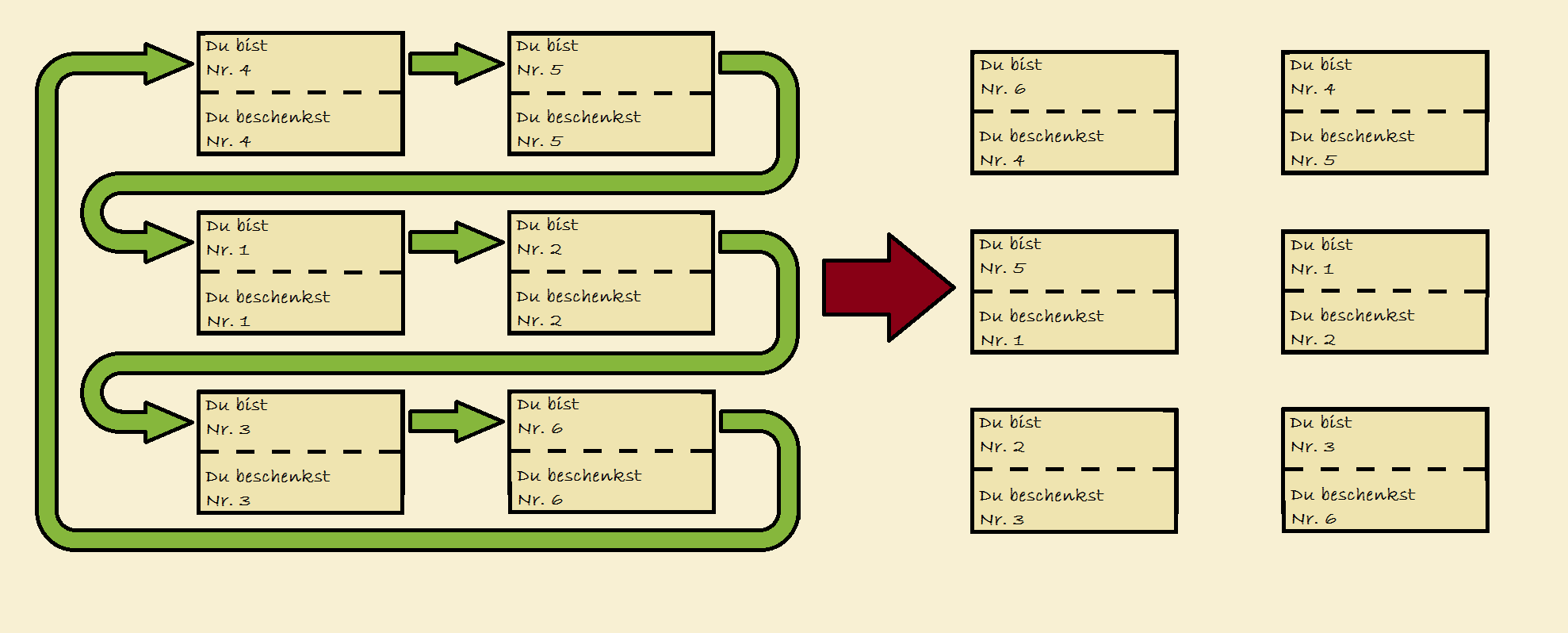
Schritt 3: Die so entstandenen neuen Zettel werden abermals gemischt und dann an die teilnehmenden Personen verteilt. Das erneute Mischen sorgt dafür, dass Informationen über die Nachbarschaft der Zettel verloren gehen.

Schritt 4: Nun trägt sich jede Person ihrer jeweiligen Nummer nach in eine Liste ein und weiß nun, wen er oder sie zu beschenken hat.

Mit dieser Methode ist gewährleistet, dass jede Konstellation zwischen zu beschenkender und schenkender Person gleichwahrscheinlich ist, unabhängig davon, in welcher Reihenfolge die Zettel gezogen wurden. Darüber hinaus ist durch Schritt 2 sichergestellt, dass niemand sich selbst beschenken muss.
Fry’s Methode ist allerdings nicht gänzlich befreit von Nachteilen: Da bei Schritt zwei der obere Teil der Zettel exakt eine Position nach rechts verschoben ist, kann man sicher davon ausgehen, dass die entstandene Permutation zykelfrei ist, das heißt, es kommt nicht vor, dass zwei Personen sich gegenseitig etwas schenken müssen. Das bedeutet insbesondere, dass man sicher sein kann, dass man kein Geschenk von der Person bekommt, die man selber beschenkt: In unserem Beispiel weiß zum Beispiel Ada, dass Sie nichts von Felix bekommen wird; Felix wiederum weiß, dass er kein Geschenk von Emmy bekommen wird, und so weiter. Fry's Methode gewährleistet daher keine absolute Anonymität.
Eine (wenn auch nicht perfekte) Möglichkeit, diese Zweierzykelfreiheit zu umgehen, besteht darin, künstlich einen Zweierzyklus (oder auch mehrere) in die Permutation einzubauen: Anstatt, dass in Schritt zwei jeder obere Teil eines Zettels um eine Position nach links verschoben wird, werden zwei zufällig gewählte obere Zettel zyklisch vertauscht, während man mit den anderen Zetteln wie gewohnt verfährt. Somit kann man am Ende nicht sicher davon ausgehen, dass die Person, die man beschenkt, nicht die Person ist, von der man ein Geschenk erhält, da man möglicherweise Teil des Zykels war. Zwar ist auf diese Weise immer noch nicht sichergestellt, dass eine solche Konstellation sich mit der eigentlich zu erwartenden Anzahl an Zweierzykeln deckt (die Wahrscheinlichkeit, Teil des einen Zykels zu sein, wird für eine große Zahl von teilnehmenden Personen beliebig klein), dafür ist die oben genannte Problematik der fehlenden Anonymität vermieden worden.
Für welche Methode Sie sich auch entscheiden mögen: Die Hauptsache ist, dass der Spaß nicht verloren geht- In diesem Sinne wünschen wir vom Medienbüro der DMV Ihnen besinnliche und vergnügliche Feiertage und ein gesundes und erfolgreiches Jahr 2019!
Hier das Video von Numberphile:



Kommentare
Danke :)