Ein Beitrag von Milena Damrau und Martin Skrodzki.
Bei den Stichworten interdisziplinäres Arbeiten und Mathematik liegen Fragen aus der Physik, den Ingenieurwissenschaften, der Informatik oder anderen Naturwissenschaften als Assoziationen nahe. Im Rahmen der Digital Humanities finden mathematische Methoden auch zunehmend in den Sozial- und Geisteswissenschaften Anwendung. Das Feld der künstlerisch arbeitenden Disziplinen, wie Malerei, Bildende Künste, Musik, um nur einige zu nennen, scheint schwieriger mit den abstrakten Inhalten der Mathematik vereinbar zu sein. Doch genau diese Kombination gelingt immer wieder und zeigt auf, wie fruchtbar eine solche Zusammenarbeit sein kann.
Auf der Jahrestagung der Deutschen Mathematiker-Vereinigung im September 2020 fand ein Minisymposium zum Thema Mathematik und Kunst statt. In zwölf Präsentationen stellten die Vortragenden unterschiedlichste Projekte vor. Viele der Vorträge sind online in einer Playlist auf YouTube verfügbar. Im Folgenden wollen wir die verfügbaren Beiträge kurz vorstellen. Damit wollen wir einerseits aufzeigen, wie groß die Themenvielfalt im Schnittbereich von Mathematik und Kunst ist. Andererseits wollen wir dazu anregen, die Vorträge anzuschauen und sich auf der nächsten Jahrestagung der DMV Ende September 2021 am zweiten Minisymposium “Mathematik und Kunst” zu beteiligen.
Mathematisches Lernen durch künstlerische Verfahren
Vielen Verfahren liegen mathematische Strukturen zu Grunde. Werden diese Prozesse nun in ihre Teile zerlegt und analysiert, ergibt sich daraus die Möglichkeit, die in ihnen enthaltene Mathematik nachzuvollziehen. Dieser Teil des Minisymposiums setzte genau dies für Webstrukturen, Kompositionen und optische Täuschungen um:
- Joshua Holden, "Markov Chains and Egyptian Tombs: Generating 'Egyptian' Tablet Weaving Designs Using Mean-Reverting Processes", https://youtu.be/hx0VDPUB6fE
- Miriam Hirt, "Stochastic Music – an Interdisciplinary Lesson Plan between Mathematics and Music", https://youtu.be/Ri3_dTRMO3Y
- Dorota Celińska-Kopczyńska und Eryk Kopczyński, "Playing with Impossibility" https://youtu.be/PD_ubxntGeU
 v.l.n.r. Simulation des Brettchenwebens (J. Holden), stochastische Komposition (M. Hirt) und eine “Escher-Treppe” (D. Celińska-Kopczyńska, E. Kopcyński).
v.l.n.r. Simulation des Brettchenwebens (J. Holden), stochastische Komposition (M. Hirt) und eine “Escher-Treppe” (D. Celińska-Kopczyńska, E. Kopcyński).
Kunstobjekte als Lern-Inspirationen
Kunst kann auch als Mittel zur Veranschaulichung mathematischer Inhalte dienen. In dieser zweiten Session stand – im Gegensatz zur ersten Session – nicht der Prozess, sondern jeweils dessen künstlerisches Endprodukt im Fokus. Veranschaulicht wurden dabei zum Beispiel geometrische Objekte unterschiedlicher Dimensionen. So wurde aus dem bekannten dreidimensionalen Würfel während einer Tanz-Performance der Tesserakt – das vierdimensionale Äquivalent des Würfels. Eine weitere Verallgemeinerung stellte Stepan Paul vor, der sich für seinen Hochschulkurs mit 3D gedruckten Skulpturen beschäftigte. Diese erleichtern es Studierenden, den Übergang von Funktionen in einer Variablen (wie aus der Schule bekannt) zu Funktionen mit zwei und mehr Variablen zu bewältigen. Die Skulptur „Big Boy Blue“ belässt es nicht beim Übergang von „eins“ zu „zwei“. Während ein normaler Torus ein Loch hat – und dann als „Donut“ bekannt ist – stellt die aus Snapology Origami zusammengesteckte Struktur einen Torus mit ganzen elf Löchern dar. Den Abschluss bildete ein Puzzle von Demian N. Goos, das nicht nur den Mathematiker Kurt Gödel zeigt, sondern auch dessen Unvollständigkeitssätze illustriert:
- Anna Maria Hartkopf und René M. Broeders, "A Mathematical Musical: 'Dimension Neukölln'" https://youtu.be/sIDZRnBcLic
- Stepan Paul, "Breaking Multivariable Calculus" https://youtu.be/D0V1Z3SqjSE
- David Honda, "Big Boy Blue – Using Snapology to Explore Mathematics" https://youtu.be/Q0gcAzzSIZo
- Demian N. Goos, "Teaching Gödel and the Limits of Mathematical Knowledge with Arts" https://youtu.be/G6IQ_gto67I
 v.l.n.r. Tanz-Performance eines Tesserakt (A.M. Hartkopf, R.M. Broeders) ©BeVoice , 3D gedruckte Skulptur bivariater Funktionen (S. Paul), der Snapology Origami Torus “Big Boy Blue” (D. Honda) und ein Puzzle zu Kurz Gödel (D.N. Goos).
v.l.n.r. Tanz-Performance eines Tesserakt (A.M. Hartkopf, R.M. Broeders) ©BeVoice , 3D gedruckte Skulptur bivariater Funktionen (S. Paul), der Snapology Origami Torus “Big Boy Blue” (D. Honda) und ein Puzzle zu Kurz Gödel (D.N. Goos).
Bildgebende Statistik und Statistik von Bildern
Zwei weitere Vortragende nutzten verschiedene statistische Methoden, um Bilder in Bezug auf unterschiedliche Fragestellungen zu analysieren. Katharina Hahn interpretiert Bildbände von Städten, deren Motive sie statistisch erfasst. In ihrer Arbeit entstehen aus den künstlerischen Werken statistische Datensätze. Loe Feijs verfährt umgekehrt. Er erarbeitet anhand statistischer Analysen der Werke von Piet Mondrian ein besseres Verständnis des Künstlers und seines Vorgehens:
- Katharina Hahn, "Photo Collages as Visual Summaries of Photo Books"
- Loe Feijs, "Analyzing the Structure of Mondrian’s 1920–1940 Compositions" https://youtu.be/opxZOdseAYs
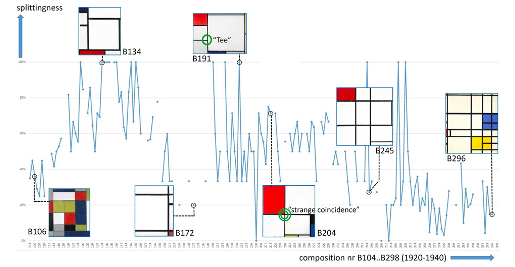 Statistische Analyse der Bilder von Piet Mondrian (L. Feijs)
Statistische Analyse der Bilder von Piet Mondrian (L. Feijs)
Symmetrie und Geometrie
Aufgrund ihrer visuellen Natur bieten sich Geometrie und Symmetrie als Grundlage für Wissenschaftskommunikation in der Mathematik an. Im letzten Teil des Minisymposiums ging es um konkrete Vermittlungsmethoden aus diesem Bereich. Die vorgestellten Lehrkonzepte unterschieden sich vor allem in ihrer Zielgruppenorientierung, indem sie sich jeweils an Kinder, Jugendliche, bzw. Studierende richten:
- Rahel Brugger, "Five-day Workshop on Ornaments" https://youtu.be/j5qJT-oVqXw
- Karl Heuer und Deniz Sarikaya, "Tilings as an Open Problem Field for Mathematically Gifted Children."
- Audrey Nasar, "Hands-on Activities for Exploring Rosette Symmetry Groups" https://youtu.be/aCmqclp0OqM
 v.l.n.r. Getöpferte Ornamente (R. Brugger), Scherenschnitte gemäß der Symmetriegruppe D3 (A. Nasar).
v.l.n.r. Getöpferte Ornamente (R. Brugger), Scherenschnitte gemäß der Symmetriegruppe D3 (A. Nasar).
Wir hoffen, dieser kleine Einblick in den Bereich “Mathematik und Kunst” hat Lust auf mehr gemacht. Ein ausführlicher Bericht zum Minisymposium erscheint auch in einer der kommenden Ausgaben der “Mitteilungen” der DMV. Wenden Sie sich gern an uns, wenn Sie Interesse am Bereich “Mathematik und Kunst” haben oder sich sogar vorstellen können, mit einem Vortrag am nächsten Minisymposium (27.09. bis 01.10. an der Universität Passau) teilzunehmen:



