Sei ε > 0. Kaum ein Beweis in der Analysis kommt ohne die Vorgabe einer beliebig kleinen, aber positiven Zahl aus, die im Laufe der Beweisführung (von einer für die Behauptung relevanten Größe) unterboten werden muss. Hinter dieser für Mathematikstudierende des ersten Semesters oftmals zermürbenden Beweisstrategie steckt eine logische Maschinerie, die die Analysis von Grund auf erneuert und in die Moderne geführt hat. Karl Weierstraß, neben Cauchy einer der Begründer dieser modernen Analysis, ist vor 125 Jahren, am 19. Februar 1897, gestorben.
Karl Weierstrass.
Foto: Freie Lizenz
Karl Theodor Wilhelm Weierstraß wurde 1815 in der münsterländischen Gemeinde Ostenfelde als Sohn des Bürgermeisters der Ortschaft geboren. 1827 zog die Familie nach Paderborn um, wo Karl das traditionsreiche „Akademische Gymnasium“ (heute Theodorianum) besuchte. Bereits als Schüler las Weierstraß die renommierte Fachzeitschrift „Journal für die reine und angewandte Mathematik“ (besser bekannt unter der Bezeichnung „Crelles Journal“).
Nach der Schule schrieb sich der Beamtensohn Weierstraß auf Wunsch seines Vaters 1834 für ein Jurastudium an der Rheinischen Friedrich-Wilhelms-Universität Bonn ein. Da Mathematik auch in seiner Bonner Zeit eine zentrale Rolle in Weierstraß‘ Leben spielte – so las er beispielsweise neben dem Studium die Arbeiten von Laplace, Abel und Jacobi – entschloss er sich, gegen den ausdrücklichen Willen seines Vaters, das Jurastudium nach vier Jahren ohne Abschluss abzubrechen und sich 1838 an der Akademie Münster, der Vorgängerin der WWU Münster, in Mathematik und Physik einzuschreiben.
In Münster begann er, sich mit abelschen Funktionen, einer Verallgemeinerung der in der Funktionentheorie untersuchten elliptischen Funktionen, zu beschäftigen, deren Theorie er wesentlich vorantreiben sollte. Er legte 1840 sein Examen ab und war ein Jahr später als Lehrer an verschiedenen preußischen Gymnasien tätig. Neben Mathematik unterrichtete er auch Physik, Botanik und Turnen.
Vom Wissenschaftsbetrieb war der nichtpromovierte Weierstraß über Jahre hinweg isoliert: Seinen ersten mathematischen Aufsatz „Zur Theorie der Abelschen Funktionen“ reichte er erst 1854 im Crelle-Journal ein. Weierstraß‘ wichtige Ergebnisse in der Funktionentheorie fanden in der Fachwelt regen Anklang; So wurde ihm unmittelbar nach seiner Veröffentlichung die Ehrendoktorwürde in Königsberg verliehen und renommierte Institute im deutschsprachigen Raum bemühten sich um die Dienste des Gymnasiallehrers. Dem Ruf der bedeutenden Mathematiker Peter Gustav Lejeune Dirichlet und Ernst Eduard Kummer aus Berlin folgend, trat Weierstraß 1856 den Weg in die preußische Hauptstadt an. Dort war er für kurze Zeit als Dozent am Königlichen Gewerbeinstitut (der heutigen Technischen Universität) angestellt, trat aber noch im gleichen Jahr eine Professur an der Friedrich-Wilhelms-Universität Berlin (der heutigen Humboldt-Universität) an.
Die Universität Berlin, Stahlstich ca. 1850
Foto: Freie Lizenz
Weierstraß avancierte schnell zu einer einflussreichen Persönlichkeit im mathematischen Berlin und galt spätestens seit den 1870er Jahren als einer der renommiertesten Mathematiker seiner Zeit. Unter der Ägide von Weierstraß, Kummer und Leopold Kronecker entwickelte sich das mathematische Institut der Universität Berlin zu einer der weltweit führenden mathematischen Forschungseinrichtungen. Zahlreiche berühmte Mathematiker*innen, unter ihnen Georg Cantor, Hermann Minkowski und Sophus Lie besuchten als Studenten Weierstraß‘ Vorlesungen.
Eine besondere Rolle unter seinen Protegés nahm Sofja Kowalewskaja ein, die 1870 auf eine Empfehlung ihres Heidelberger Professors und Förderers, dem Mathematiker und Weierstraß-Schüler Leo Koenigsberger hin als potenzielle Doktorandin an Weierstraß herantrat.
Sofja Wassiljewna Kowalewskaja
Foto: Freie Lizenz
Da sie als Frau nicht an der Berliner Universität angenommen werden durfte, beschloss Weierstraß, dem eine große Sympathie für das russische Ausnahmetalent nachgesagt wird, Kowalewskaja privat zu unterrichten und sie in ihren Promotionsbestrebungen zu unterstützen. Wegen guter Kontakte Weierstraß‘ zum dortigen mathematischen Institut gelang es ihr schließlich, sich als Promotionsstudentin an der Universität Göttingen einzuschreiben und erhielt ihren Doktortitel 1874 – als erste Frau der Mathematikgeschichte. Zehn Jahre später wurde Sofja Kowalewskaja, ebenfalls als erste Frau der Mathematikgeschichte, ordentliche Professorin an der Universität Stockholm. Unterstützung fand sie dabei von Gösta Mittag-Leffler, dem damals führenden Mathematiker des Landes und ebenfalls einer von Weierstraß‘ Schülern. Weierstraß und Kowalewskaja führten eine zwanzig Jahre währende intensive Brieffreundschaft: Bis zum Tod Kowalewskajas 1891 hatten beide mehr als 160 Briefe ausgetauscht.
Neben der Funktionentheorie war das Hauptarbeitsgebiet des oftmals „Vater der modernen Analysis“ genannten Weierstraß‘ die Grundlagenforschung in der Analysis. Vor seinen wegweisenden Arbeiten und Vorlesungen war die Analysis weit davon entfernt, die exakte mathematische Disziplin von heute zu sein: Man hantierte mit unendlich kleinen Zahlen, definierte Eigenschaften analytischer Objekte mit Hilfe von logisch nicht fassbaren Bewegungsmetaphern wie „strebt gegen“ oder „beliebig nah“ und ließ sich in Beweisen nicht selten von der Intuition leiten. Durch die Einführung der sogenannten „Epsilontik“ (benannt nach dem griechischen Buchstaben Epsilon, der in Definitionen und Beweisen in der Analysis für eine beliebige, bzw. beliebig kleine positive reelle Zahl steht) gelang es Weierstraß, die Definitionen der grundlegenden Eigenschaften analytischer Objekte, wie die der Stetigkeit einer Funktion oder die der Konvergenz einer Folge, gänzlich von vagen und unpräzisen Elementen zu befreien und so die Analysis auf ein logisch fundiertes Fundament zu heben; eine intuitive und mathematisch unpräzise Beschreibung der Stetigkeit einer reellwertigen Funktion mit Hilfe von Nähe-, Sprung- oder Strebt-gegen-Metaphern etwa wich der Weierstraß'schen Epsilon-Delta-Definition der Stetigkeit (siehe Infobox).
Sei \(\Omega\) eine offene Teilmenge von \(\mathbb{R}\), z.B. das Intervall \((0,1)\) oder \(\mathbb{R}\) selber und sei \(f\) eine auf \(\Omega\) definierte, reell- oder komplexwertige Funktion. Sei \(x_0\in \Omega\). Dann ist nennen wir \(f\) stetig in \(x_0\), wenn:
Für jede Zahl \(\epsilon>0\)
eine Zahl \(\delta>0\) existiert,
sodass für jedes \(x\in \Omega\) gilt:
Wenn \(|x-x_0|<\delta\), dann gilt auch \(|f(x)-f(x_0)|<\epsilon\)
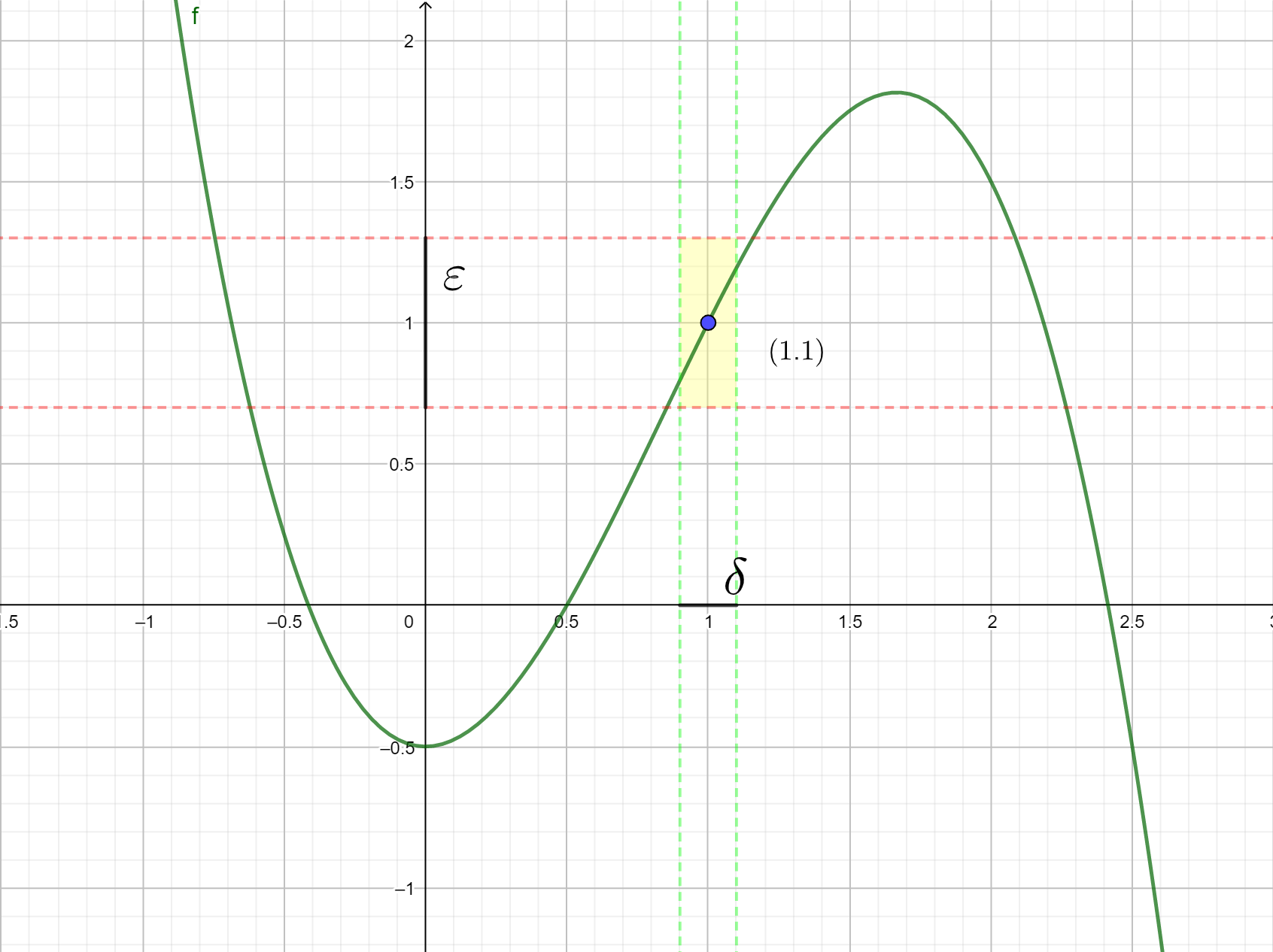Eine stetige Funktion. Anschaulich bedeutet Stetigkeit an der Stelle \(x=1\): Man kann um den Punkt \((1,1)\) ein Rechteck mit einer beliebigen, vorgegebenen Höhe so zeichnen, dass der Graph der Funktion das Rechteck zur linken und zur rechten Seite des Rechtecks (und nicht etwa zur oberen oder unteren) verlässt. Eigene Abbildung
Da klare Definitionen präzise Beweise erst möglich machen, haben Weierstraß‘ Arbeiten und Vorlesungen auch den Beweisen in der Analysis eine nie dagewesene Präzision und Exaktheit verleihen können; die sprichwörtliche „Weierstraß'sche Strenge“ wurde zum Ideal der mathematisch und logisch exakten Beweisführung in der Analysis erkoren.
Ein weiterer Vorteil der Weierstraß'schen Fundierung der Analysis ist, dass eine intuitionsunabhängige Analysis in der Lage ist, wahre Aussagen beweisen zu können, die der Intuition zunächst zu widersprechen scheinen: Man ging zum Beispiel aufgrund graphischer Evidenz lange davon aus, dass stetige Funktionen, abgesehen von einigen isolierten Punkten, auch überall differenzierbar sind und es daher keine (überall) stetigen Funktionen geben kann, die nirgendwo differenzierbar sind.
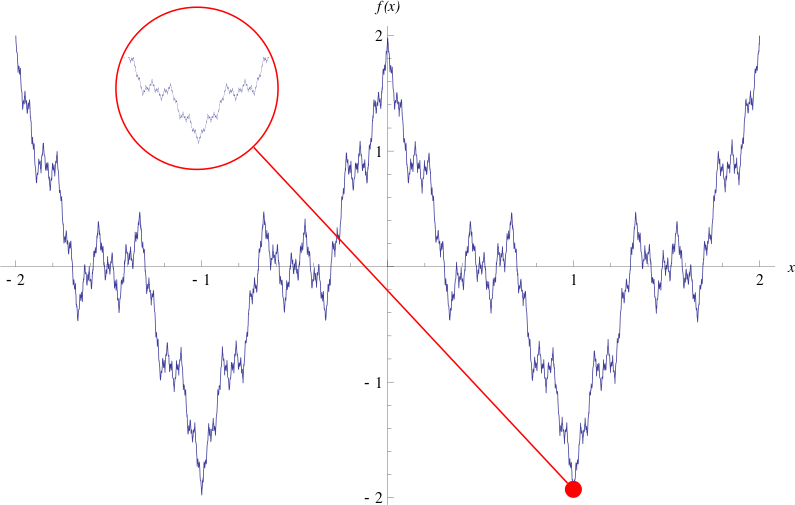Der Graph einer stetigen, aber nirgendwo differenzierbaren Funktion: Egal wie nah man in den Funktionsgraphen hineinzoomt, nie gelangt man zu einer glatten Stelle. Die Fachwelt war so schockiert über die Existenz solcher Funktionen, dass sie ihr den Namen Weierstraß'sches Monster gab.
Abb.: Freie Lizenz
Tatsächlich lässt sich aber, wenn man in der Lage ist, eine präzise Definition von den Begriffen Stetigkeit und Differenzierbarkeit anzugeben, mit „Weierstraß'scher Strenge“ beweisen, dass zum Beispiel die Funktion \(f:x\mapsto \sum_{k=1}^\infty\frac{2^k\sin(2^k x)}{3^k}\) zwar übertall stetig, aber überraschenderweise nirgendwo differenzierbar sein kann. Weniger überraschend ist hingegen die Tatsache, dass es Karl Weierstraß war, der als erstes ein Beispiel für eine derartige Funktion der Fachöffentlichkeit vorstellte.
Konrad Krug