Weihnachten naht.
Da wollen auch wir - wie jedes Jahr - einen Beitrag zur mathematischen Papiersternproduktion leisten.

Doch zunächst geht es nicht um Sterne, sondern um Laternen. Oder Stiefel. Nehmen wir eine DIN-A4-Seite und falzen sie nach folgendem Muster entlang der Linien - blaue Linien geben "Täler" und rote "Berge". Anschließend rollen wir das Papier so zusammen, dass es am grau markierten Streifen zusammengeklebt werden kann.
Wie von Zauberkand ergibt sich ein Zylinder, der in Dreiecke unterteilt ist.

Das Ganze sieht ein wenig aus wie eine Laterne, und tatsächlich ist es in der mathematischen Welt als "Schwarzsche Laterne" bekannt - oder auch als "Schwarzscher Stiefel", denn die Form erinnert ebenfalls an einen 80er-Jahre-Stiefel aus geknautschtem Leder. Offenbar waren solche Stiefel schon in den hundert Jahre zuvor auf den Straßen zu sehen, damals veröffentlichte nämlich Hermann Amandus Schwarz (1843-1921) 1883 eine kleine dreiseitige Arbeit darüber, unter dem Titel "Sur une définition erronée de l'aire d'une surface courbe", also etwa "über eine irrige Definition der Oberfläche einer gekrümmten Fläche".
Weshalb irrig? Schwarz wollte keine Laternen oder Stiefelschäfte basteln - tatsächlich kommt weder das eine noch das andere Wort in dem Artikel vor - er hatte sich die Oberfläche des Körpers angesehen, und dabei entdeckte er eine Seltsamkeit. Die Zerlegung in Dreiecke konnte offensichtlich zu irrigen Ergebnissen führen. Wie groß ist denn diese Fläche?
Zunächst nehmen wir uns ein regelmäßiges n-Eck, dessen Ecken auf einem Kreis vom Radius r liegen. Wir stapeln m-1 Kopien solcher n-Ecke im Abstand h/m parallel übereinander, so dass alle Ecken auf dem Mantel eines Kreiszylinders vom Radius r und Höhe h zu liegen kommen. Dann verdrehen wir jedes zweite n-Eck um den Winkel pi/n und verbinden alle benachbarten Ecken zu Dreiecken.
Man sieht leicht, dass die Form dann aus 2mn identischen Dreiecken besteht.

Nun beginnt elementare Trigonometrie.
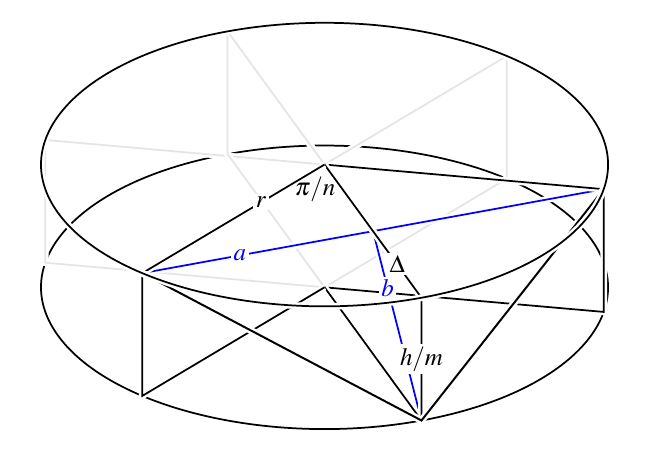
Wir suchen die Werte für a und b, Grundlinie und Höhe des Dreiecks.
a ist zugleich die Grundline eines gleichschenkligen Dreiecks, dessen andere Seiten beide r lang sind. Der Winkel dazwischen ist 2pi/n. Also gilt a = 2 r sin(pi/n).
Für b beobachten wir zunächst, dass cos(pi/n) = (r-Delta)/r = 1 - Delta/r gilt; umgeformt ergibt sich Delta = r(1 - cos(pi/n)).
Außerdem erhalten wir mit Hilfe des Satzes von Pythagoras, dass (h/m)^2 + Delta^2 = b^2 gilt - oder: b^2 = (h/m)^2 + r^2(1 - cos(pi/n))^2.
Die Fläche eines Dreiecks ist also:
r sin(pi/n) ( (h/m)^2 + r^2(1 - cos(pi/n))^2 )^(1/2)
und die Fläche des ganzen Körpers beträgt damit:
F(m,n) := 2 m n r sin(pi/n) ( (h/m)^2 + r^2(1 - cos(pi/n))^2 )^(1/2).
Wenn wir nun m und n immer größer wählen, dann wird sich die Laternenoberfläche immer weiter an den Zylinder anschmiegen, dachte Schwarz:

Also müsste man ja im Grenzwert die Oberfläche eines Zylinders, also 2 r pi h erhalten. Doch überrascht stellte er fest: Das muss nicht passieren. Lässt man m ebenso schnell wie n wachsen, dann schmiegt sich die Oberfläche tatsächlich brav an den Zylinder an:
lim_n->oo F(n,n) = 2 r pi h
Für die allgemeinere Betrachtung wählen wir nun m(n) als Funktion in Abhängigkeit von n und ziehen 1/m(n) aus der Wurzel heraus.
F(m,n) := 2 n r sin(pi/n) ( h^2 + m^2 r^2 (1 - cos(pi/n))^2 )^(1/2).
Jetzt schätzen wir die wesentlichen Teile in der Wurzel ab - und nehmen dabei die Taylor-Entwicklung des Cosinus zu Hilfe.
lim_n->oo |m(n) (1 - cos(pi/n))| = lim_n->oo |m(n) m(n) (- sum_i=1^oo (-1)^i/(2i)! (pi/n)^(2i) )| <= lim_n->oo |m(n) pi^2/(2n^2)|
Das geht genau dann gegen Null, wenn m(n) in O(n^2) ist. Falls das der Fall ist, dann wird der Wert unter der Wurzel h und wir erhalten mit n sin(pi/n -> pi tatsächlich den Grenzwert:
2 r pi h
Falls nicht - falls also m(n) schneller wächst als n^2 - dann wächst die Oberfläche ins Unendliche. Noch ein Körper also mit unendlicher Oberfläche und endlichem Volumen...

Genau solche Fallstricke bei der Diskretisierung kontinuierlicher Oebrflächen werden aktuell zum Beispiel im Sonderforschungsbereich Diskretisierung in Geometrie und Dynamik untersucht.
Im Hinblick auf Weihnachten sollte man also für eine Schwarzsche Laterne am Weihnachtsbaum m(n) tunlichst langsamer als n^2 wachsen lassen. Sonst braucht man unendlich viel Transparentapier, um endliches Volumen zu umhüllen! Und dasselbe gilt (mit festerem Papier) natürlich auch für den Schwarzschen Nikolausstiefel.
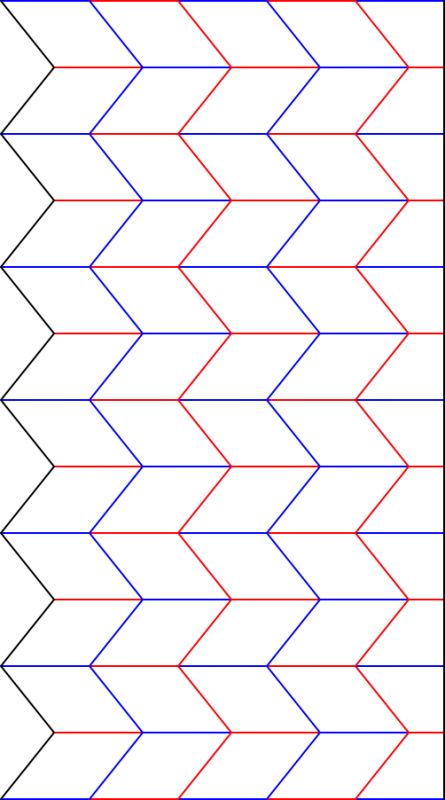
Man kann aber noch viel mehr machen. Das Faltmuster lässt sich auch um 90 Grad drehen, etwas variieren (entdecken Sie, was dabei genau passiert?) und falten - und man erhält eine näherungsweise zylindrische Laterne wie rechts im Bild, etwas anders als die Schwarzsche Laterne. (Man kann mit anderen Faltschnitten auch hübsche bauchige Vasen oder Laternen erzeugen. Wie man das macht, wird vielleicht mal ein anderer Post erklären.)
Man muss das gefaltete Papier aber auch nicht in Zylindergeometrie aufwickeln. Nehmen wir folgendes Faltschema - wieder sind "Täler" blau und "Berge" rot. Drucken Sie das Schema dreimal aus und falten Sie es. Kleben Sie dann die drei Stücke zu einer langen "Zieharmonika" zusammen, die sich zu etwas formen lässt, das dem zentralen Stern im Bild ganz oben ähnelt. (Die gerade Seite bildet den Mittelpunkt.)
Viel Spaß - und eine fröhliche Vorweihnachtszeit!

Euer Andreas Loos



