Heute ist der 80. Geburtstag von
John Nash. (Bekannt aus dem Film 'A beautiful Mind', in dem es freilich mehr um Schizophrenie als um Mathematik geht.)
Das paßt deshalb gerade gut in diese Reihe, weil wir hier verschiedene Anwendungen des
Borsuk-Ulam-Theorems besprochen hatten. (Das war der Satz aus
Teil 12, daß es auf der Sphäre zwei antipodale Punkte mit gleicher Temperatur und gleichem Luftdruck gibt.)
Von Nash stammt ein überraschender Beweis dieses topologischen Satzes mit Hilfe des 1947
von Nash (und unabhängig bereits 1942 von Piet Hein)
entwickelten Spiels 'Hex'.
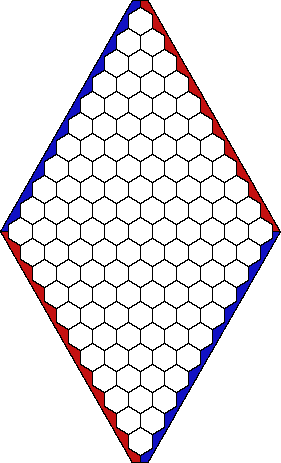
Hex spielen zwei Spieler auf einem viereckigen Brett, das mit 6-Ecken gepflastert ist. Die beiden Spieler, Rot und Blau, setzen abwechseln einen Stein auf eines der Felder. Ziel von Rot ist es, eine Reihe von roten Steinen zwischen den beiden gegenüberliegenden roten Kanten zu legen. Entsprechend für Blau, und jeder versucht natürlich den anderen zu behindern. Eine mögliche Schlußstellung, in der Rot gewonnen hat, zeigt das folgende Bild.
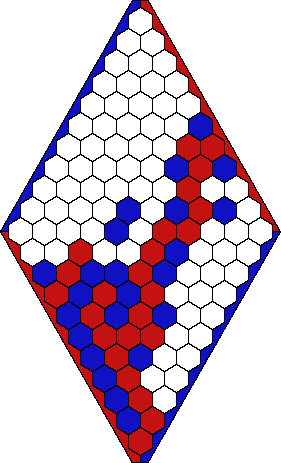
Nash bewies, daß es bei diesem Spiel
immer einen Sieger geben muß. (Es gibt also keine Spiele, bei denen sich beide Gegner gegenseitig alle Möglichkeiten verbauen.) Bemerkenswerterweise kann man zeigen, daß daraus das
Borsuk-Ulam-Theorem folgt, so daß Nash sozusagen spielend einen Beweis dieses Theorems gefunden hat.
(David Gale (1979). "The Game of Hex and Brouwer Fixed-Point Theorem". The American Mathematical Monthly 86: 818-827.)
Nashs Beweis zeigt zwar,
daß der erste Spieler immer gewinnen kann, aber nicht
wie. Tatsächlich kennt man explizite Gewinnstrategien wohl nur für Bretter mit maximal 7x7 Feldern.
Noch einige Worte zu Nashs anderen Arbeiten:
Den
Wirtschafts-Nobelpreis erhielt er für seine Doktorarbeit, in der die Existenz von
Nash-Gleichgewichten gezeigt wurde. Aus mathematischer Sicht ist dies eine Anwendung des
Kakutani-Fixpunktsatzes (eine kompliziertere Variante des Brouwerschen Fixpunktsatzes, auf den wir in dieser Serie auch noch kommen werden und den man übrigens auch aus dem Borsuk-Ulam-Theorem herleiten kann).
Unter Mathematikern ist es ein weitverbreiteter Konsens, daß die Doktorarbeit, für die er den Nobelpreis erhielt, bei weitem nicht die schwierigste von Nashs mathematischen Arbeiten ist. Als solche gilt wohl eher seine Arbeit über die
Regularität der Lösungen parabolischer partieller Differentialgleichungen. Es gibt natürlich auch Wissenschaftler (speziell Spieltheoretiker), die dies
vehement bestreiten.
Ein sehr spektakulärer Satz von Nash war sein
Einbettungssatz. Dieser besagt zum Beispiel, daß sich jede Fläche
isometrisch in eine beliebig kleine Kugel einbetten läßt. ('Isometrisch' heißt, daß Abstände auf der Fläche sich nicht ändern: die Fläche wird nicht einfach zusammengestaucht.) Für einen studierten Mathematiker ist dieser Satz scheinbar absurd: wenn die Fläche in eine Kugel vom Radius ε eingebettet ist und den Rand der Kugel berührt, dann ist im Berührpunkt die
Krümmung der Fläche mindestens 1/ε2. Wenn man die Fläche in beliebig kleine Kugeln einbetten kann, müßte die Krümmung beliebig groß sein, offenbar ein Widerspruch. Die Auflösung dieses Widerspruchs ist, daß Nashs Einbettungen
nur 1-mal differenzierbar sind. Krümmung ist aber nur für 2-mal differenzierbare Flächen definiert und damit ergibt sich doch kein Widerspruch zu Nashs Konstruktion.
Nash hat übrigens auch noch beweisen, daß es für jede Fläche 2-mal differenzierbare Einbettungen in den euklidischen Raum gibt. (Wenn auch eben nicht in eine beliebig kleine Kugel.) Aus der Wikipedia:
The first theorem is for C1-smooth embeddings and the second for analytic or of class Ck, 2 ≤ k ≤ ∞. These two theorems are very different from each other; the first one has a very simple proof and is very counterintuitive, while the proof of the second one is very technical but the result is not at all surprising.
Nash hatte sich durch solche Arbeiten den Ruf erworben, scheinbar absurde Behauptungen aufzustellen, die sich aber (mit technisch sehr anspruchsvollen und schwerverständlichen Beweisen) als richtig herausstellen. Wie man z.B. bei Nasar nachlesen kann, führte dies dann dazu, daß es zunächst kaum auffiel, als er ab Ende der 50er Jahre wirklich erkrankte. Z.B. berichtete jemand über ein AMS-Meeting, auf dem Nash über angebliche Lösungsansätze der Riemann-Vermutung vortrug: "
Ein Wort paßte nicht zum anderen. [...] es war dummes Geschwätz, eine völlig verrückte Mathematik. [...] Einige bemerkten es nicht einmal. Man geht zu diesen Treffen und läßt die Vorträge über sich ergehen. Dann geht man hinaus, schnappt sich jemanden und versucht herauszufinden, was man gerade gehört hat."
Weiteres über Nashs Biographie findet man in
Sylvia Nasars Buch 'Auf den fremden Meeren des Denkens' bzw. in der Taschenbuchausgabe unter dem etwas reißerischen Titel 'Genie und Wahnsinn'. (Die Erklärungen zu Nashs wissenschaftlichen Arbeiten sind dort allerdings ziemlich verworren, jedenfalls wenn man als Leser nicht sowieso schon weiß, um was es geht.)
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "https://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
var pageTracker = _gat._getTracker("UA-4708238-1");
pageTracker._initData();
pageTracker._trackPageview();
 Hex spielen zwei Spieler auf einem viereckigen Brett, das mit 6-Ecken gepflastert ist. Die beiden Spieler, Rot und Blau, setzen abwechseln einen Stein auf eines der Felder. Ziel von Rot ist es, eine Reihe von roten Steinen zwischen den beiden gegenüberliegenden roten Kanten zu legen. Entsprechend für Blau, und jeder versucht natürlich den anderen zu behindern. Eine mögliche Schlußstellung, in der Rot gewonnen hat, zeigt das folgende Bild.
Hex spielen zwei Spieler auf einem viereckigen Brett, das mit 6-Ecken gepflastert ist. Die beiden Spieler, Rot und Blau, setzen abwechseln einen Stein auf eines der Felder. Ziel von Rot ist es, eine Reihe von roten Steinen zwischen den beiden gegenüberliegenden roten Kanten zu legen. Entsprechend für Blau, und jeder versucht natürlich den anderen zu behindern. Eine mögliche Schlußstellung, in der Rot gewonnen hat, zeigt das folgende Bild.
 Nash bewies, daß es bei diesem Spiel immer einen Sieger geben muß. (Es gibt also keine Spiele, bei denen sich beide Gegner gegenseitig alle Möglichkeiten verbauen.) Bemerkenswerterweise kann man zeigen, daß daraus das Borsuk-Ulam-Theorem folgt, so daß Nash sozusagen spielend einen Beweis dieses Theorems gefunden hat. (David Gale (1979). "The Game of Hex and Brouwer Fixed-Point Theorem". The American Mathematical Monthly 86: 818-827.)
Nashs Beweis zeigt zwar, daß der erste Spieler immer gewinnen kann, aber nicht wie. Tatsächlich kennt man explizite Gewinnstrategien wohl nur für Bretter mit maximal 7x7 Feldern.
Noch einige Worte zu Nashs anderen Arbeiten:
Den Wirtschafts-Nobelpreis erhielt er für seine Doktorarbeit, in der die Existenz von Nash-Gleichgewichten gezeigt wurde. Aus mathematischer Sicht ist dies eine Anwendung des Kakutani-Fixpunktsatzes (eine kompliziertere Variante des Brouwerschen Fixpunktsatzes, auf den wir in dieser Serie auch noch kommen werden und den man übrigens auch aus dem Borsuk-Ulam-Theorem herleiten kann).
Unter Mathematikern ist es ein weitverbreiteter Konsens, daß die Doktorarbeit, für die er den Nobelpreis erhielt, bei weitem nicht die schwierigste von Nashs mathematischen Arbeiten ist. Als solche gilt wohl eher seine Arbeit über die Regularität der Lösungen parabolischer partieller Differentialgleichungen. Es gibt natürlich auch Wissenschaftler (speziell Spieltheoretiker), die dies vehement bestreiten.
Ein sehr spektakulärer Satz von Nash war sein Einbettungssatz. Dieser besagt zum Beispiel, daß sich jede Fläche isometrisch in eine beliebig kleine Kugel einbetten läßt. ('Isometrisch' heißt, daß Abstände auf der Fläche sich nicht ändern: die Fläche wird nicht einfach zusammengestaucht.) Für einen studierten Mathematiker ist dieser Satz scheinbar absurd: wenn die Fläche in eine Kugel vom Radius ε eingebettet ist und den Rand der Kugel berührt, dann ist im Berührpunkt die Krümmung der Fläche mindestens 1/ε2. Wenn man die Fläche in beliebig kleine Kugeln einbetten kann, müßte die Krümmung beliebig groß sein, offenbar ein Widerspruch. Die Auflösung dieses Widerspruchs ist, daß Nashs Einbettungen nur 1-mal differenzierbar sind. Krümmung ist aber nur für 2-mal differenzierbare Flächen definiert und damit ergibt sich doch kein Widerspruch zu Nashs Konstruktion.
Nash hat übrigens auch noch beweisen, daß es für jede Fläche 2-mal differenzierbare Einbettungen in den euklidischen Raum gibt. (Wenn auch eben nicht in eine beliebig kleine Kugel.) Aus der Wikipedia: The first theorem is for C1-smooth embeddings and the second for analytic or of class Ck, 2 ≤ k ≤ ∞. These two theorems are very different from each other; the first one has a very simple proof and is very counterintuitive, while the proof of the second one is very technical but the result is not at all surprising.
Nash hatte sich durch solche Arbeiten den Ruf erworben, scheinbar absurde Behauptungen aufzustellen, die sich aber (mit technisch sehr anspruchsvollen und schwerverständlichen Beweisen) als richtig herausstellen. Wie man z.B. bei Nasar nachlesen kann, führte dies dann dazu, daß es zunächst kaum auffiel, als er ab Ende der 50er Jahre wirklich erkrankte. Z.B. berichtete jemand über ein AMS-Meeting, auf dem Nash über angebliche Lösungsansätze der Riemann-Vermutung vortrug: "Ein Wort paßte nicht zum anderen. [...] es war dummes Geschwätz, eine völlig verrückte Mathematik. [...] Einige bemerkten es nicht einmal. Man geht zu diesen Treffen und läßt die Vorträge über sich ergehen. Dann geht man hinaus, schnappt sich jemanden und versucht herauszufinden, was man gerade gehört hat."
Weiteres über Nashs Biographie findet man in Sylvia Nasars Buch 'Auf den fremden Meeren des Denkens' bzw. in der Taschenbuchausgabe unter dem etwas reißerischen Titel 'Genie und Wahnsinn'. (Die Erklärungen zu Nashs wissenschaftlichen Arbeiten sind dort allerdings ziemlich verworren, jedenfalls wenn man als Leser nicht sowieso schon weiß, um was es geht.)
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "https://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
var pageTracker = _gat._getTracker("UA-4708238-1");
pageTracker._initData();
pageTracker._trackPageview();
Nash bewies, daß es bei diesem Spiel immer einen Sieger geben muß. (Es gibt also keine Spiele, bei denen sich beide Gegner gegenseitig alle Möglichkeiten verbauen.) Bemerkenswerterweise kann man zeigen, daß daraus das Borsuk-Ulam-Theorem folgt, so daß Nash sozusagen spielend einen Beweis dieses Theorems gefunden hat. (David Gale (1979). "The Game of Hex and Brouwer Fixed-Point Theorem". The American Mathematical Monthly 86: 818-827.)
Nashs Beweis zeigt zwar, daß der erste Spieler immer gewinnen kann, aber nicht wie. Tatsächlich kennt man explizite Gewinnstrategien wohl nur für Bretter mit maximal 7x7 Feldern.
Noch einige Worte zu Nashs anderen Arbeiten:
Den Wirtschafts-Nobelpreis erhielt er für seine Doktorarbeit, in der die Existenz von Nash-Gleichgewichten gezeigt wurde. Aus mathematischer Sicht ist dies eine Anwendung des Kakutani-Fixpunktsatzes (eine kompliziertere Variante des Brouwerschen Fixpunktsatzes, auf den wir in dieser Serie auch noch kommen werden und den man übrigens auch aus dem Borsuk-Ulam-Theorem herleiten kann).
Unter Mathematikern ist es ein weitverbreiteter Konsens, daß die Doktorarbeit, für die er den Nobelpreis erhielt, bei weitem nicht die schwierigste von Nashs mathematischen Arbeiten ist. Als solche gilt wohl eher seine Arbeit über die Regularität der Lösungen parabolischer partieller Differentialgleichungen. Es gibt natürlich auch Wissenschaftler (speziell Spieltheoretiker), die dies vehement bestreiten.
Ein sehr spektakulärer Satz von Nash war sein Einbettungssatz. Dieser besagt zum Beispiel, daß sich jede Fläche isometrisch in eine beliebig kleine Kugel einbetten läßt. ('Isometrisch' heißt, daß Abstände auf der Fläche sich nicht ändern: die Fläche wird nicht einfach zusammengestaucht.) Für einen studierten Mathematiker ist dieser Satz scheinbar absurd: wenn die Fläche in eine Kugel vom Radius ε eingebettet ist und den Rand der Kugel berührt, dann ist im Berührpunkt die Krümmung der Fläche mindestens 1/ε2. Wenn man die Fläche in beliebig kleine Kugeln einbetten kann, müßte die Krümmung beliebig groß sein, offenbar ein Widerspruch. Die Auflösung dieses Widerspruchs ist, daß Nashs Einbettungen nur 1-mal differenzierbar sind. Krümmung ist aber nur für 2-mal differenzierbare Flächen definiert und damit ergibt sich doch kein Widerspruch zu Nashs Konstruktion.
Nash hat übrigens auch noch beweisen, daß es für jede Fläche 2-mal differenzierbare Einbettungen in den euklidischen Raum gibt. (Wenn auch eben nicht in eine beliebig kleine Kugel.) Aus der Wikipedia: The first theorem is for C1-smooth embeddings and the second for analytic or of class Ck, 2 ≤ k ≤ ∞. These two theorems are very different from each other; the first one has a very simple proof and is very counterintuitive, while the proof of the second one is very technical but the result is not at all surprising.
Nash hatte sich durch solche Arbeiten den Ruf erworben, scheinbar absurde Behauptungen aufzustellen, die sich aber (mit technisch sehr anspruchsvollen und schwerverständlichen Beweisen) als richtig herausstellen. Wie man z.B. bei Nasar nachlesen kann, führte dies dann dazu, daß es zunächst kaum auffiel, als er ab Ende der 50er Jahre wirklich erkrankte. Z.B. berichtete jemand über ein AMS-Meeting, auf dem Nash über angebliche Lösungsansätze der Riemann-Vermutung vortrug: "Ein Wort paßte nicht zum anderen. [...] es war dummes Geschwätz, eine völlig verrückte Mathematik. [...] Einige bemerkten es nicht einmal. Man geht zu diesen Treffen und läßt die Vorträge über sich ergehen. Dann geht man hinaus, schnappt sich jemanden und versucht herauszufinden, was man gerade gehört hat."
Weiteres über Nashs Biographie findet man in Sylvia Nasars Buch 'Auf den fremden Meeren des Denkens' bzw. in der Taschenbuchausgabe unter dem etwas reißerischen Titel 'Genie und Wahnsinn'. (Die Erklärungen zu Nashs wissenschaftlichen Arbeiten sind dort allerdings ziemlich verworren, jedenfalls wenn man als Leser nicht sowieso schon weiß, um was es geht.)
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "https://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
var pageTracker = _gat._getTracker("UA-4708238-1");
pageTracker._initData();
pageTracker._trackPageview(); 


