Topologie von Flächen XIX
Eine mathematische Spielerei: was passiert, wenn man den Drehimpuls der Erde stetig erhöht?
Seit Newton weiß man, daß die Erde nicht rund, sondern oval ist. Der Durchmesser am Äquator (ca. 12700 km) ist um 40 Kilometer länger als der vom Nordpol zum Südpol gemessene Durchmesser.
Hervorgerufen wird dies durch die Erdrotation, genauer durch die Zentrifugalkraft senkrecht zur Drehachse. Für einen Festkörper hätte diese Zentrifugalkraft keinen Einfluß auf die Form, aber die Erde ist wegen ihres geschmolzenen Inneren kein Festkörper. (Außerdem spielen die Bewegungen der tektonischen Platten noch eine Rolle.)
Bekanntlich übt die Gezeitenreibung eine bremsende Wirkung auf die Drehbewegung der Erde aus, wodurch die Tageslänge immerhin um ca. 17 Mikrosekunden im Jahr zunimmt. Man geht davon aus, daß vor 4 Milliarden Jahren die Länge eines Tages nur 14 Stunden betrug.
Zumindestens theoretisch kann man natürlich auch die Frage diskutieren, was eigentlich passieren würde, wenn der Drehimpuls der Erde nicht verringert, sondern erhöht werden würde. Welche Auswirkungen würde dies auf die Form der Erde haben?
Der bekannte Mathematiker Etienne Ghys hat vor einiger Zeit in einem öffentlichen Vortrag diese theoretische Frage erörtert, welche Auswirkungen ein steigender Drehimpuls auf die Form der Erde hätte. Der folgende Text ist eine Zusammenfassung dieses Vortrags.
Zur Klarstellung: es handelt sich hier um eine mathematisch und physikalisch korrekte Spielerei, die natürlich keine praktischen Anwendungen hat. Die Erde wird etwas vereinfacht als rotierende ideale Flüssigkeitsmenge im Vakuum aufgefaßt (dies ist vernünftig, weil die Erdkruste tatsächlich recht dünn ist), man vernachläßigt also Inhomogenitäten und interne Flüße.
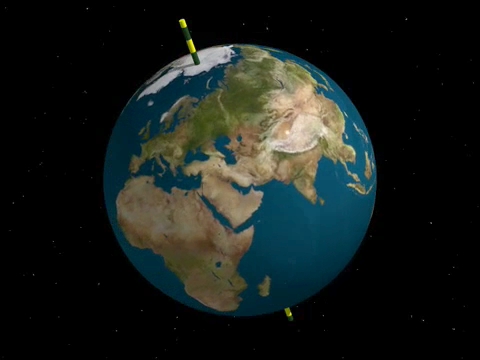 omega=0.06 L=0.024
MacLaurin hatte bereits 1742 in "A Treatise of Fluxions" nachgerechnet, daß bei steigendem Drehimpuls die Erde immer flacher wird. Sie wird zu einem Ellipsoid mit zwei gleichen und einer kürzeren Achse, und rotiert um die kürzere Achse.
Die maximale Geschwindigkeit wird bei einem um 20% höheren Radius erreicht (nämlich das 11-fache unserer heutigen Erdgeschwindigkeit), danach nimmt die Geschwindigkeit wieder ab.
omega=0.06 L=0.024
MacLaurin hatte bereits 1742 in "A Treatise of Fluxions" nachgerechnet, daß bei steigendem Drehimpuls die Erde immer flacher wird. Sie wird zu einem Ellipsoid mit zwei gleichen und einer kürzeren Achse, und rotiert um die kürzere Achse.
Die maximale Geschwindigkeit wird bei einem um 20% höheren Radius erreicht (nämlich das 11-fache unserer heutigen Erdgeschwindigkeit), danach nimmt die Geschwindigkeit wieder ab.
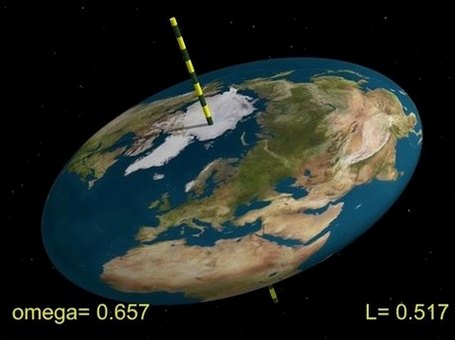 Erstaunlicherweise ist dies aber nicht der einzige mögliche Effekt. Zu bestimmten Zeitpunkten haben die Differentialgleichungen mehrere Lösungen, so daß es mehrere Möglichkeiten gibt, wie sich weiter entwickelt. (Dies bezeichnet man als 'Bifurkation'.)
Jacobi hatte schon 1834 gezeigt, daß dadurch Übergänge zu Ellipsoiden mit drei unterschiedlichen Achsen möglich sind.
Erstaunlicherweise ist dies aber nicht der einzige mögliche Effekt. Zu bestimmten Zeitpunkten haben die Differentialgleichungen mehrere Lösungen, so daß es mehrere Möglichkeiten gibt, wie sich weiter entwickelt. (Dies bezeichnet man als 'Bifurkation'.)
Jacobi hatte schon 1834 gezeigt, daß dadurch Übergänge zu Ellipsoiden mit drei unterschiedlichen Achsen möglich sind.
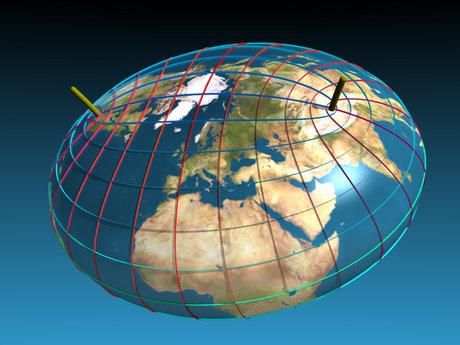 Poincare beschrieb 1885 in "Sur l'équilibre d'une masse fluide animée d'un mouvement de rotation" weitere multiple Bifurkationen, letztlich erhält man durch diese eine birnenförmige Sphäre.
Poincare beschrieb 1885 in "Sur l'équilibre d'une masse fluide animée d'un mouvement de rotation" weitere multiple Bifurkationen, letztlich erhält man durch diese eine birnenförmige Sphäre.
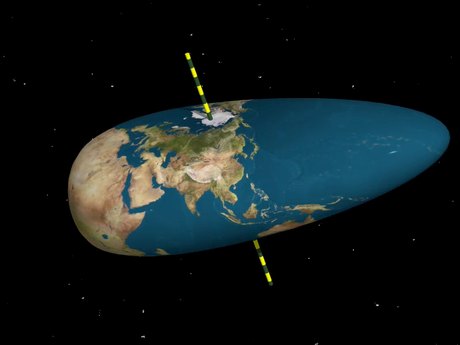 Die letzten beiden Bilder sind Möglichkeiten, die bei Erhöhung des Drehimpulses auftreten können, aber nicht müssen. So etwas nennt man Bifurkation. (Aus der Wikipedia: "Nichtlineare Systeme, deren Verhalten von einem Parameter abhängt, können bei einer Änderung des Parameters ihr Verhalten plötzlich ändern. Zum Beispiel kann ein System, das zuvor einem Grenzwert zustrebte, nun zwischen zwei Werten hin und her springen, also zwei Häufungspunkte aufweisen. Dies nennt man eine Bifurkation.") Die Theorie solcher Bifurkationen war besonders in den 70er Jahren unter dem griffigen Namen Katastrophentheorie sehr populär.
Quelle: The shape of Planet Earth, Bilder von Jos Leys
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17, Teil 18
Die letzten beiden Bilder sind Möglichkeiten, die bei Erhöhung des Drehimpulses auftreten können, aber nicht müssen. So etwas nennt man Bifurkation. (Aus der Wikipedia: "Nichtlineare Systeme, deren Verhalten von einem Parameter abhängt, können bei einer Änderung des Parameters ihr Verhalten plötzlich ändern. Zum Beispiel kann ein System, das zuvor einem Grenzwert zustrebte, nun zwischen zwei Werten hin und her springen, also zwei Häufungspunkte aufweisen. Dies nennt man eine Bifurkation.") Die Theorie solcher Bifurkationen war besonders in den 70er Jahren unter dem griffigen Namen Katastrophentheorie sehr populär.
Quelle: The shape of Planet Earth, Bilder von Jos Leys
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17, Teil 18



