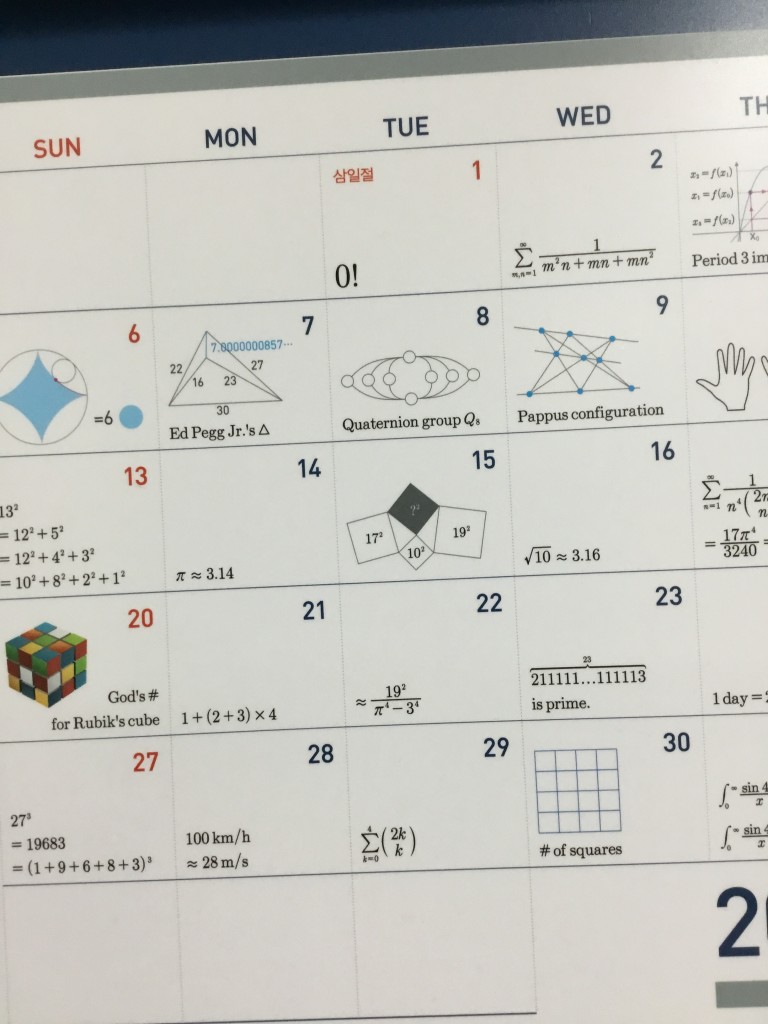
Fourierreihen, Riemann Zeta und die Quaternionengruppe. Die Reihe bei der 2 sollte sich mit zweimaliger Partialbruchzerlegung berechnen lassen (siehe hier), der Eintrag bei der 3 (Bild unten) bezieht sich auf den Satz von Sarkovskii und der bei der 4 auf den 4-Farben-Satz. Ed Pegg Jr. fand seinerzeit zahlreiche Dreieckszerlegungen, bei denen nicht nur die Seitenlänge des Dreiecks, sondern auch die Längen der teilenden Strecken jeweils ganze Zahlen sind. Eine Liste von Beispielen gibt es hier. Das Dreieck bei der 7 ist aber keines. Die Quaternionengruppe Q₈ besteht aus den 8 Einheitsquaternionen also \(\pm1,\pm i,\pm j,\pm k\). Das Bild zeigt ihren Zykelgraphen: die Kreise entsprechen den 8 Gruppenelementen, die Zykel im Graphen bestehen aus den Potenzen jeweils eines Elements. Der Satz von Pappus besagt dass für das Bild bei der 9 die drei in der Mitte liegenden Schnittpunkte wieder auf einer gemeinsamen Geraden liegen. Die 12 ist die maximale Anzahl 3-dimensionaler Einheitskugeln, die eine weitere Einheitskugel berühren ohne dass Überschneidungen auftreten. Die Gleichung bei der 17 ist eine Anwendung der Formel für zeta(4), die man z.B. mit Fourier-Reihenentwicklung beweisen kann. Der Zauberwürfel kann aus jeder Position in höchstens 20 Zügen gelöst werden. Bei der 26 geht es um die sogenannten minimalen Primzahlen, die keinen Substring haben, der selbst eine Primzahl ist. Daraus folgt dann, dass jede Primzahl eine dieser 26 Primzahlen als Substring enthält. Wer Beweise zu 31 hat, möge sie als Kommentar posten.

Um einen Kommentar zu verfassen, müssen Sie sich einloggen bzw. kurz als Gast registrieren.