Im Studium haben wir hauptsächlich mit vier Zahlen gearbeitet: 0, 1, Pi, e. Eine 7 begegnet einem da selten. aus "Von wegen Kopfrechnen", Badische Neueste Nachrichten, 3. September 2017

Siebenen in der Mathematik

Siebenen in der Mathematik, als erstes fallen einem da wohl die berühmten 28 unterschiedlichen Differentialstrukturen auf der 7-dimensionalen Sphäre ein, mit denen John Milnor 1956 zur Überraschung der Fachwelt bewies, dass es auf ein und derselben topologischen Mannigfaltigkeit sehr unterschiedliche Arten der Differentialrechnung geben kann. Gut, man kännte sagen, die besondere Rolle der 7 ist da nur ein historischer Zufall. Schließlich gibt es exotische Sphären auch in den meisten anderen Dimensionen. Eine besondere Eigenschaft, die die 7-dimensionale Sphäre nur noch mit den Sphären in Dimension 0, 1 und 3 gemeinsam hat, ist aber die Existenz einer Basis aus nichtverschwindenden Vektorfeldern und damit zusammenhängend die Existenz einer stetigen Multiplikation (Lie-Gruppen-Struktur). Die wiederum ist der Grund, warum der Rⁿ nur für n=1,2,4,8 eine reelle Divisionsalgebra sein kann, warum es also nach reellen Zahlen, komplexen Zahlen, Quaternionen und Oktonionen nicht mehr weitergeht. 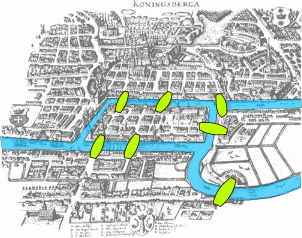Geht man historisch nochmal zwei Jahrhunderte zurück, dann standen die sieben Brücken von Königsberg 1736 am Anfang der Graphentheorie. Und die Zahl 7 ist hier wirklich von Bedeutung: im heutigen Kaliningrad gibt es noch 5 Brücken und jetzt sind Spaziergänge, bei denen jede Brücke genau einmal überquert wird, dann doch möglich. Allerdings kehren sie nicht zum Ausgangspunkt zurück; in mathematischer Terminologie: es gibt einen Eulerweg, aber keinen Eulerkreis. Sieben ist auch die Antwort auf manche Fragen der elementaren Wahrscheinlichkeitstheorie, etwa der nach dem wahrscheinlichsten Ereignis beim Wurf mit zwei Würfeln. In der projektiven Geometrie hat die Fano-Ebene P²F₂ als kleinste projektive Ebene sieben Punkte und sieben Geraden. Und n=7 ist die kleinste Generatorzahl, hat also ein interessantestes Muster in der Dezimaldarstellung der Vielfachen von 1/n: deren sich periodisch wiederholenden Ziffernfolgen sind alle aus den sechs Ziffern 1-4-2-8-5-7 zusammengesetzt. Was einem zugegebenermaßen im Studium tatsächlich nicht begegnet, ebenso wenig wie die Teilbarkeitsregeln der 7 oder die diversen mit der 7 verbundenen Kopfrechentricks.

Kein Buch mit sieben Siegeln

Erstmals auf Deutsch ausgestrahlt wurde am 21. Oktober bei ARTE die BBC-Dokumentation "Climate change by numbers", die den Klimawandel von Mathematikern statt von Klimaforschern erklären läßt und sich dabei auf drei Zahlen fokussiert:

0,85 Grad 95 Prozent 10¹² Tonnen

Also den Anstieg der globalen Durchschnittstemperatur gegenüber 1880, die im IPCC-Report angegebene Wahrscheinlichkeit, dass mehr als die Hälfte der Erderwärmung vom Menschen verursacht sei, und die Menge Kohlenstoff, die wir noch verbrennen können bevor es zu ernsthaften Klimaveränderungen kommt. Wobei es in der einstündigen Sendung dann vor allem darum ging, wie diese Zahlen gewonnen werden und was sie "wirklich" bedeuten. Also beispielsweise warum man (erst) seit 1880 zuverläßige Temperaturmessungen hat und wie man Mathematik nutzt, um fehlende Daten zu rekonstruieren.

Die Weisheit hat ihr Haus gebaut, ihre sieben Säulen behauen

Es hilft, wenn man Zahlen grob überschlagen kann: Geht das überhaupt auf, was da jetzt vorgeschlagen wird?

sagte Wolfgang Schäuble der Frankfurter Allgemeinen Sonntagszeitung über die erforderlichen Qualifikationen seines Nachfolgers. Passend dazu kramten dann YouTuber eine fünf Jahre alte Rede des damals gerade als FDP-Kandidaten für das Amt gehandelten Politikers mit dem schönen Versprecher Eins und eins ist eins und nicht drei heraus. In eine ähnliche Richtung geht die von der Süddeutschen Zeitung in einem Artikel "Digitalisierung an Schulen" vom 16. Juni aufgeworfene Frage.

Sollen [die Schulen] weiterhin lehren, wer Pythagoras war und wie sich dessen berühmter Satz mathematisch beweisen läßt? Oder ist es, wie manche Google-Manager empfehlen, sinnvoller, vor allem Technologieunterricht zu erteilen? Schlie\ss lich läßt sich heute mit wenigen Mausklicks klären, wie lang die Diagonale eines Rechtecks ist.

Ich habe mal nachgeschaut, was man mit dem Suchbegriff "Diagonale im Rechteck berechnen" bei Google bekommt. Der erste Treffer ist zwar noch ein herkömmlicher Lexikoneintrag, die nächsten 4 Treffer sind dann aber ausnahmslos Kalkulatoren, wo man nur die Seitenlängen eingeben muss und das Ergebnis bekommt.

Sieben Rechensünden

Einiges Aufsehen erregte vor sieben Jahren eine Studie der britischen Regierung, derzufolge 49,1 Prozent der erwachsenen Briten geringere Rechenfertigkeiten haben als sie von 9- bis 11-jährigen erwartet werden, während das beim Lesen und Schreiben nur auf 14,9 Prozent zuträfe. Erklärt das das Abstimmungsergebnis beim Brexit? Vergleichbare Studien in Deutschland scheint es nicht zu geben. Der "Hohlspiegel" des SPIEGEL präsentiert aber regelmäßig Beispiele wie die folgenden sieben aus der deutschen Presse. Im Juli scheitert die Frank­fur­ter All­ge­mei­ne Sonn­tags­zei­tung in einem Artikel über die Fan­ta­sy­se­rie {\em Game of Thro­nes} an den Grundrechenarten:

Die kom­men­den fünf­zehn Epi­so­den - sie­ben in Staf­fel sie­ben, sechs in Staf­fel acht - wer­den un­ter die­se Spe­ku­la­ti­on ei­nen Schlußstrich set­zen.

Und bei ndr.de hapert es sogar an einfachen Größenvergleichen:

Neun der acht An­ge­klag­ten ei­ner mut­maß­li­chen Geld­au­to­ma­ten-Ban­de ha­ben ein Ge­ständ­nis ab­ge­legt.

Immerhin erst beim Stoff der Sekundarschule strauchelt die dpa:

Vor al­lem Wirt­schafts­wis­sen­schaft­ler wer­den der­zeit ge­sucht. Erst­mals seit 2011 ge­hören sie zu den am häu­figs­ten ge­such­ten Fach­kräf­ten. Fast je­des fünf­te Stel­len­an­ge­bot (4,5 Pro­zent) rich­tet sich an sie.

Im Vergleich damit geradezu subtil ist dann schon die Prozentrechnung der Frankfurter Rundschau: Heißt das jetzt, mehr als 122 Prozent der Deutschen können keine Prozentrechnung? Oder doch nur:

Ich dachte, Du regelst das Finanzielle. Häh, was? Ich verlass mich doch immer auf Dich!

Bei der unten abgebildeten Überschrift aus der Hildesheimer Allgemeinen Zeitung frage ich mich, ob das nur ein Zahlendreher ist oder die redegewandten Banker es inzwischen schaffen, den mitstenografierenden Journalisten eine Halbierung der Dividende als Verdoppelung zu verkaufen? "Warum kann der nesciens se numerare animus nur bis fünf und nicht bis sieben zählen?" fragte schon 1822 die Neue Musikalische Zeitung - und gab die Antwort: "... in der Harmonik machte niemand Glück damit".

Ist Sieben normal?

Es ist ja eigentlich schon ein alter Hut, die Geschichte vom Kulturverteidiger, der auf die Fangfrage nach arabischen Ziffern hereinfällt und dann zwangsweise wieder mit den kultureigenen römischen Ziffern rechnen muss. Eine neue Version davon gab es jetzt doch noch einmal Ende August auf einer Wahlkampfveranstaltung zur Bürgermeisterwahl im saarländischen Völklingen. Der Vertreter der Spaß partei "Die Partei" wies dort den örtlichen NPD-Kandidaten darauf hin, dass in Völklingen viele Hausnummern mit arabischen Zahlen gekennzeichnet seien und fragte ihn, wie er gegen diese schleichende Überfremdung vorgehen wolle. Der reagierte prompt:

Da warten Sie ab, Herr Faust, wenn ich Oberbürgermeister bin, dann werde ich das ändern, da werden dann mal normale Zahlen drankommen.

Normale Zahlen sind bekanntlich reelle Zahlen, unter deren Nachkommaziffern für jedes \(k \ge 1\) alle möglichen k-stelligen Ziffernblöcke mit gleichen asymptotischen relativen Häufigkeiten auftreten. (https://de.wikipedia.org/wiki/Normale Zahl) Der Wunsch des NPD-Kandidaten dürfte nicht schwer zu erfüllen sein: seit Emile Borel wissen wir, dass fast alle Zahlen normal sind - die nicht normalen Zahlen bilden eine Menge vom Lebesgue-Maß Null. Ob man dann auch π als Hausnummer verwenden dürfte ... das ist ein immer noch ungelöstes Problem der Zahlentheorie. Bekannte normale Zahlen, die die NPD also als Hausnummern genehmigen würde, sind aber jedenfalls 0,2357111317192329313741434753... oder 0123456789101112131415.... Letztere entsteht durch Hintereinanderschreiben der arabischen Ziffernfolgen aller natürlichen Zahlen.

Um einen Kommentar zu verfassen, müssen Sie sich einloggen bzw. kurz als Gast registrieren.