Bei einem Schlaganfall zählt jede Sekunde. Ärzte und Ärztinnen stehen in diesem Moment unter massivem Druck, da sie so schnell wie möglich Entscheidungen treffen, gleichzeitig aber auch die individuellen Besonderheiten des Patienten oder der Patientin genau im Blick haben sollen. Dies ist in der Stresssituation eines Schlaganfalls oft nicht in vollem Ausmaß möglich, da unter solch enormem Zeitdruck häufig keine komplexen Fallabwägungsprozesse machbar sind. Das neue Computermodell eines Forschungsteams der Berliner Charité bietet hier eine bisher ungenutzte Chance. Das Tool operiert auf Basis des maschinellen Lernens und wurde mit Hilfe tausender Daten und Krankheitsverläufe von Schlaganfallpatient*innen trainiert. Innerhalb von nur 20 Minuten kann nun auf Grundlage dieser Daten eine mathematisch basierte, personalisierte Schlaganfallbehandlung erstellt werden. Mathematische Forschung kann hier zum Lebensretter werden.^[1]

Der Klimawandel treibt das Schmelzen der Polarkappen in einem besorgniserregenden Tempo voran. Der Rückgang des Eises im Nordpolarmeer gilt als einer der wichtigsten Parameter in der Klimaforschung. Hier kommen nicht nur die klassischen Klimaforschenden zum Einsatz, sondern auch Mathematiker*innen befassen sich, beispielsweise am Alfred-Wegener-Institut für Polarforschung in Bremerhaven, intensiv mit dem arktischen Meereis. Die exakte Erfassung und Berechnung der Meereisausdehnung gestalten sich durch diverse Effekte dieser Materie als schlichtweg unmöglich. Mit Hilfe von mathematischen Modellen können jedoch zumindest Näherungswerte der Meereisausdehnung für die Klimaforschung bereitgestellt werden. Klimamodelle werden genauer und Voraussagen können optimiert werden. Mathematiker*innen werden somit zum entscheidenden Partner im Kampf gegen den Klimawandel.^[2]

Die mathematische Forschung beschäftigt sich nicht nur mit den großen Phänomenen und Problemen der Menschheit, sondern durchaus auch mit dem Geschäft der Kleinsten. Die Babywindel als High-Tech-Entwicklung – diese wird am Fraunhofer-Institut für Techno- und Wirtschaftsmathematik in Kaiserslautern erforscht. Auf dem Weg von der Stoffwindel zur High-Tech-Windel ist jede Menge mathematische Forschung in dieses Produkt geflossen. Das Augenmerk liegt hier vor allem auf Vliesen, welche die Flüssigkeit absorbieren und heute doppelt so viel aufnehmen können wie noch vor 20 Jahren. Die Ergebnisse der „Windelforschung“ sind nicht nur für die Hygieneindustrie von Relevanz, sondern finden beispielsweise auch in der Autoindustrie oder der Gesundheitsbranche Anwendung.^[3]

 

Zum Wert mathematischer Forschung

Der Wert mathematischer Forschung und von Mathematik für die Gesellschaft und für die deutsche Volkswirtschaft ergibt sich nicht immer im Moment einer neuen wissenschaftlichen Entdeckung oder einer Entwicklung. Teils kommt es zwischen theoretischer Erkenntnis und Anwendung in der Praxis zu einer Verzögerung, in einigen Fällen sogar von mehreren Jahrzehnten. Für viele mathematische Erkenntnisse, beispielsweise im Bereich der kryptographischen Kodierungstheorie, lässt sich der Wert gar nicht mehr ermessen, da sie zu einem gesellschaftlichen Allgemeingut geworden sind.

Mathematikerin am Institut für Mathematik der Freien Universität Berlin. Foto: Bernd Wannenmacher

Der britische Mathematiker Godfrey Hardy hat sich seinerzeit damit gerühmt, dass es sich bei seiner Forschung auf dem Gebiet der Zahlentheorie um die „reine Mathematik“ handelt, welche keinerlei Anwendung finden wird. Mittlerweile stellt seine Zahlentheorie die Grundlage der modernen, mathematischen Kryptographie dar, welche vor allem im Kontext von sicherheitsrelevanten Fragen des Verarbeitens, Übertragens und Benutzens von Informationen zum Tragen kommt.

Wie dieses Beispiel verdeutlicht, lässt sich der ideelle und materielle Wert von mathematischer Forschung nur schwer prognostizieren. Mathematische Erkenntnisse finden teils erst Jahre nach ihrer Entdeckung eine konkrete Anwendung im Alltag. Andere Errungenschaften hingegen, welche explizit für eine bestimmte Anwendung entwickelt wurden, verlieren an Bedeutung im Zuge des wissenschaftlich-technologischen Fortschritts. Zahllose Entwicklungen des heutigen Alltags, insbesondere im Hinblick auf unsere hochtechnisierte Welt, gehen auf mathematische Grundlagenforschung zurück, auch wenn diese mal mehr und mal weniger lange zurückliegt. Mathematische Grundlagenforschung zahlt sich nicht immer sofort aus, aber um langfristig neue Erkenntnisse und Innovationen zu erreichen, darf die Grundlagenforschung nicht zugunsten aktueller Trends vernachlässigt werden.^[4] 

Die mathematische Forschung beschäftigt sich, oft in Zusammenarbeit mit den anderen Technik- und Naturwissenschaften, mit den großen Fragen unserer Zukunft, die häufig im Bereich von Nachhaltigkeit, Sicherheit oder auch der Medizin stehen. Mathematische Forschung ist die Grundlage für Computersimulationen und Datenanalysen verschiedenster Art. Diese sind bei der Beschäftigung mit den Fragen der Zukunft nicht mehr wegzudenken, da die zu erforschenden Szenarien immer abstrakter, aber auch komplexer werden. Der Jahresbericht der Deutschen Forschungsgemeinschaft 2020 verdeutlicht in diesem Zusammenhang noch einmal die fundamentale Rolle der Mathematik in Projekten zur Erforschung unseres Lebensraums:

 

„In einem Gutteil dieser Projekte ergaben – und ergeben – die Untersuchungen mit modernen Methoden oft große Datenmengen, die zu interpretieren nur mithilfe mathematischer Modelle möglich ist. Die Mathematik hat neben ihrem immerwährenden intrinsischen Forschungsanspruch daher im Zeitalter der hochdurchsatz- und datengetriebenen Forschung einen neuen Stellenwert als Querschnittswissenschaft gewonnen.“^[5]

 

Mathematik als Querschnittswissenschaft prägt uns seit Generationen und wird auch an der Beantwortung der Fragestellungen der Zukunft maßgeblich beteiligt sein. Mathematik als anwendungsbezogene Wissenschaft und Treiber von Innovation bietet die entscheidenden Grundlagen für Entwicklung, nachhaltige Lösungsansätze, Wertschöpfung und gesellschaftlichen Wohlstand.

 

Mathematische Forschung in Zahlen

Die mathematische Forschung in Deutschland hat erfreulicherweise in den letzten Jahren an Unterstützung gewonnen, bleibt jedoch in manchen Bereichen aufgrund fehlender Ressourcen noch hinter ihren Möglichkeiten zurück. Dieses Kapitel soll den Fokus auf die mathematische Forschungslandschaft in Deutschland richten, denn sie ist der Grundpfeiler für Fortschritt und Entwicklung der Industrienation und des Forschungsstandortes Deutschland.

Die Ausgaben für Forschung und Entwicklung (FuE) in Deutschland steigen seit der Jahrtausendwende erfreulicherweise kontinuierlich an. Die FuE-Quote lag 2019 bei 3,17%, sodass Deutschland bereits 2017 das Ziel von 3% erreicht hat, welches im Rahmen der europäischen Wachstumsstrategie Europa 2020 vereinbart wurde.^[6]

 

Infobox: MaRDI Wie werden mathematische Forschungsdaten eigentlich organisiert? Mathematische Forschungsdaten werden immer umfangreicher, komplexer und vielfältiger. Dies ist insbesondere bei der Anwendung von Mathematik in interdisziplinären Kontexten der Fall. Umso wichtiger ist es, standardisierte Datenformate zu schaffen, die eine gegenseitige Nutzbarkeit von Daten (Interoperabilität) sicherzustellen, und Programmierschnittstellen für Anwendungen zu entwickeln. Bisher standen Daten oft nur lokal, projektbezogen und temporär zur Verfügung. Mit der Nationalen Forschungsdateninfrastruktur (NFDI) werden Datenbestände von Wissenschaft und Forschung systematisch erschlossen, vernetzt und nachhaltig nutzbar gemacht. Hierzu stellen Bund und Länder Mittel für die Förderung von Konsortien zur Verfügung, welche auf verschiedene Wissenschaftsdisziplinen zugeschnittene Strategien entwickeln, um ein Forschungsdatenmanagement nach den FAIR-Prinzipien zu etablieren. Diesem Auftrag auch für die Mathematik nachzukommen, ist die Mission von MaRDI (Mathematical Research Data Initiative), einer Konsortialinitiative der mathematischen Wissenschaften, welche Standards für die mathematische Community etablieren, eine mathematische Datenbibliothek aufbauen und die dafür benötigen Dienstleistungen in Form eines Service-Portals bereitstellen möchte. Das Ziel von MaRDI ist, die FAIR-Prinzipien (Findable, Accessible, Interoperable, Reusable) in allen Bereichen der Mathematik und ihren Anwendungen zu etablieren. Relevante mathematische Daten können hierbei Dokumente, domain-spezifische wissenschaftliche Software-Pakete und ihre Bibliotheken, Computer Algebra Systeme, Sammlungen mathematischer Modelle, Data Frames und Simulationsdaten und vieles mehr sein. Das Konsortium wird vom Berliner Weierstraß-Institut für Angewandte Analysis und Stochastik (WIAS) koordiniert. Ihm gehören derzeit weitere 23 Partner (Universitäten und Forschungsinstitute, Wissenschafts-Infrastruktureinrichtungen, Exzellenzcluster sowie die Deutsche Mathematiker-Vereinigung und die European Mathematical Society) an. [7] Mehr Informationen zu MaRDI gibt es hier.

 

Abb. 1. Bruttoinlandsausgaben für Forschung und Entwickung nach finanzierenden Sektoren und Anteil am Bruttoinlandsprodukt 2005 und 2015 - 2019 ^[8]

In Europa gehört Deutschland gemessen an der jährlichen Wirtschaftsleistung mit einer FuE-Quote von 3,17 % (2019) zu den Ländern mit den höchsten Ausgaben in diesem Bereich und übertrifft damit auch die USA. Im Jahr 2020 betrug die durchschnittliche FuE-Quote der EU-28-Länder 2,3 %. In Europa verzeichneten nur Belgien und Schweden (je 3,5%) und Österreich (3,22%) eine höhere Quote als Deutschland.^[9] Weltweite Spitzenreiter sind derzeit Israel (4,94%), Südkorea (4,53%) und Japan (3,26%).^[10] Bis 2025 sollen in Deutschland mindestens 3,5% des BIP in Forschung und Entwicklung investiert werden.

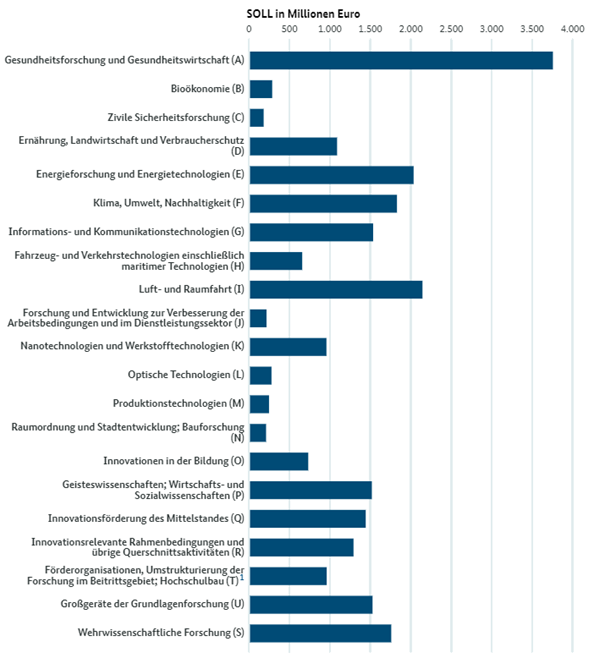
Der mit Abstand größte Förderbereich des Bundes ist die Gesundheitsforschung und Gesundheitswirtschaft. Dahinter folgen die Luft- und Raumfahrt, die Energieforschung und Energietechnologien, der Bereich Klima, Umwelt und Nachhaltigkeit sowie auch die wehrwissenschaftliche Forschung. Knapp dahinter liegen die Förderbereiche Großgeräte der Grundlagenforschung, Geistes-, Wirtschafts- und Sozialwissenschaften, Informations- und Kommunikationstechnologien sowie Innovationsförderung des Mittelstandes. Wie die Fallbeispiele zu Beginn dieses Kapitels zeigen, findet Mathematik Eingang in alle diese Förderbereiche. Bis auf wenige Ausnahmen in den Geisteswissenschaften sind alle anderen Förderbereiche auf mathematische Forschung angewiesen oder treiben mathematische Forschung und Entwicklung selbst voran.

Ausgaben des Bundes für Forschung und Entwicklung nach Förderbereichen und Förderschwerpunkten im Jahr 2021 (Soll in Millionen Euro):

Abb. 2. Ausgaben des Bundes für Forschung und Entwicklung nach Sektoren 2021 ^[11]

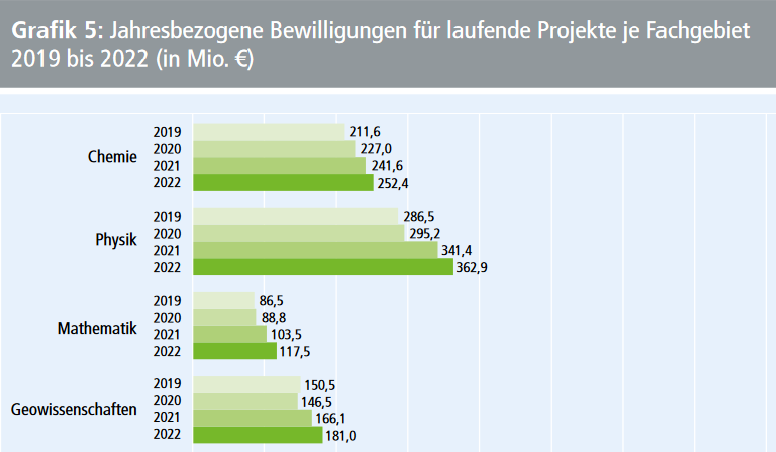
Für die mathematische Forschung in Deutschland sind Drittmittel eine wichtige Finanzierungsquelle, um Entwicklung und Innovation voranzutreiben.^[12] Einer der wichtigsten Geber von Drittmitteln ist hierbei die Deutsche Forschungsgemeinschaft (DFG). In den letzten Jahren sind die jahresbezogenen Bewilligungen für laufende Projekte in der Mathematik erfreulicherweise gestiegen (Abb. 3, unten). Waren es 2019 noch 86,5 Millionen Euro an jahresbezogenen Bewilligungen für laufende Projekte, erhielt die Mathematik im Jahr 2022 bereits 117,5 Millionen Euro. Diese beziehen sich auf die für das betreffende Jahr bewilligten Summen. Es wäre zu hoffen, dass sich der positive Trend fortsetzt, insbesondere in Anbetracht der zunehmenden Wichtigkeit mathematischer Forschung für die drängenden Zukunftsfragen.

Abb. 3. Jahresbezogenen Bewilligungen für laufende Projekte in den Naturwissenschaften je Fachgebiet 2019 - 2022 ^[13]

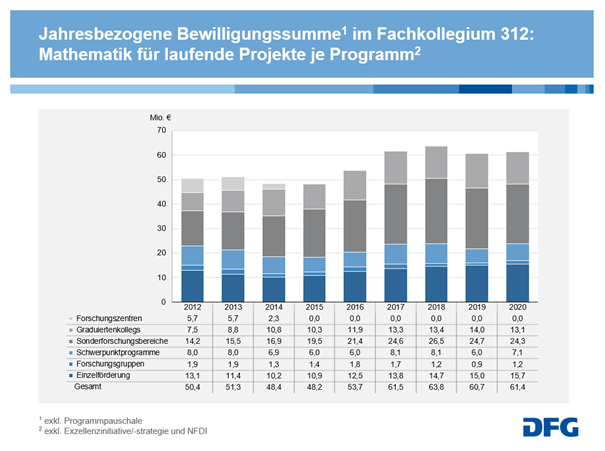
Einen Überblick über die Verteilung der Drittmittel der DFG in der Mathematik auf die verschiedenen Förderprogramme (Abb. 4, unten) erhält man bei der Betrachtung der jahresbezogenen Bewilligungssummen nach Programmart. Nicht berücksichtigt sind in dieser Abbildung die NFDI (Nationale Forschungsdateninfrastrukturen) und insbesondere auch nicht die Exzellenzinitiative bzw. Exzellenzstrategie mit vergleichsweise hohen Fördervolumina. Der größte Anteil der jahresbezogenen Bewilligungssumme im Fach Mathematik geht an die Sonderforschungsbereiche. Ein großer Anteil der jährlichen Bewilligungen geht auch an die Graduiertenkollegs und fließt somit in die Nachwuchsförderung. In Anbetracht des Mangels an Mathematiker*innen auf dem Arbeitsmarkt ist dies äußert begrüßenswert.

Abb. 4. Jahresbezogene Bewilligungssumme  im Fachkollegium 312 ^[14], Bereich Mathematik, von 2012 bis 2020. Quelle: DFG

Betrachtet man die im jeweiligen Jahr entschiedene Bewilligungsquote (Abb. 5, unten), d.h. das Verhältnis der Bewilligungssumme zur Antragssumme von allen eingereichten Anträgen in der Mathematik, so liegt diese Quote mit 28% leider etwas unter dem Wert von 2017 (32% Bewilligungsquote). Die dargestellten Summen ergeben sich jeweils aus den Gesamtsummen der berücksichtigten Anträge, die für die gesamte Dauer des jeweiligen Vorhabens beantragt bzw. bewilligt wurden, welche sich in der Regel über mehrere Jahre erstreckt.

Abb. 5. Antrags- und Bewilligungssummen sowie Bewilligungsquoten in der Einzelförderung im Bereich Mathematik 2012 - 2020 ^[15]

Laut dem DFG Förderatlas ist die Universität Bonn mit dem Hausdorff Center for Mathematics (HCM) eindeutig der bewilligungsstärkste Standort der Mathematik. An zweiter und dritter Stelle finden sich die Universitäten Münster und Bielefeld. Eine weitere Größe in der mathematischen Forschung stellt der Verbund aus TU Berlin, HU Berlin und FU Berlin, welche zusammen mit den außeruniversitären Einrichtungen Weierstraß-Institut für Angewandte Analysis und Stochastik (WIAS) und dem Zuse-Institut Berlin das DFG-geförderte Exzellenzcluster MATH+ bilden. Die klassische Unterteilung in reine und angewandte Mathematik bildet dabei die Forschungsrealität kaum mehr ab.

 

Infobox: Standorte mathematischer Forschung in Deutschland DFG Exzellenzcluster Titel Ort Schwerpunkt MATH+: The Berlin Mathematics Research Center Freie Universität Berlin Humboldt-Universität zu Berlin Technische Universität Berlin Interdisziplinärer und institutionenübergreifender Forschungsverbund, an dem die gesamte Berliner Mathematik beteiligt ist. Hausdorff Center for Mathematics Rheinische Friedrich-Wilhelms-Universität Bonn Forschungseinrichtung, die von den vier mathematischen Instituten an der Rheinischen Friedrich-Wilhelms-Universität Bonn, vom Max-Planck-Institut für Mathematik und vom Institut für Gesellschafts- und Wirtschaftswissenschaften getragen wird. Mathematik Münster: Dynamik - Geometrie - Struktur Westfälische Wilhelms-Universität Münster Identifikation und Analyse der zugrundeliegenden Struktur eines gegebenen Problems, dessen geometrische Betrachtung und die Analyse relevanter Dynamiken von Gruppen- und Halbgruppen-Aktionen. Strukturen: Emergenz in Natur, Mathematik und komplexen Daten Ruprecht-Karls-Universität Heidelberg „Strukturen“ erforscht neue Konzepte und Methoden, um zu verstehen, wie Struktur, kollektive Phänomene und Komplexität aus den grundlegenden Gesetzen der Physik hervorgehen. Außeruniversitäre Forschungsinstitute: Institut Ort Schwerpunkt Fraunhofer-Institut für Techno- und Wirtschaftsmathematik (ITWM) Kaiserslautern Techno- und Wirtschaftsmathematik. Brücke zwischen Hochschule und Industriepartner. Fraunhofer-Institut für Algorithmen und Wissenschaftliches Rechnen SCAI St. Augustin Computational Science und Optimierung. Informationsextraktion aus großen Datenbeständen. Kombiniert mathematisches und informatorisches Wissen mit Schwerpunkt in der Algorithmik. Weierstraß-Institut für Angewandte Analysis und Stochastik Berlin Projektorientierte Verknüpfung der mathematischen Disziplinen Analysis, Stochastik und Numerik. Mathematisches Forschungsinstitut Oberwolfach (MFO) Oberwolfach Mathematische Forschung, wissenschaftliche Zusammenarbeit und Fortbildung in der Mathematik sowie ihren Grenzgebieten. Max-Planck-Institut für Mathematik Bonn Forschung zur reinen Mathematik. Max-Planck-Institut für Mathematik in den Naturwissenschaften Leipzig Mathematik im Hinblick auf Anwendungen in den Naturwissenschaften (v.a. Physik, Biologie, Chemie und Materialwissenschaften). Zuse Institute  Berlin Interdisziplinäre, angewandte Mathematik und datenintensives High-Performance-Computing. Liste interdisziplinärer Forschungsinstitute mit ausgeprägtem mathematischem Anteil: Institut Ort Schwerpunkt Max-Planck-Institut für Dynamik komplexer technischer Systeme Magdeburg Erforschung von allen Aspekten der Systemverfahrenstechnik (chemische Verfahrenstechnik, Bioprozesstechnik und Energiesysteme). Max-Planck-Institut für Gravitationsphysik Potsdam-Golm Erforschung des gesamten Spektrums der Gravitationsphysik. Fraunhofer Institut für digitale Medizin (MEVIS) Bremen Entwicklung von Softwaresystemen für die bild- und datengestützte Früherkennung, Diagnose und Therapie in der Medizin. Max-Planck-Institut für Plasmaphysik Garching und Greifswald Untersuchung der Grundlagen für ein Fusionskraftwerk, das – ähnlich wie die Sonne – Energie aus der Verschmelzung leichter Atomkerne gewinnen soll. HITS gGmbH Heidelberger Institut für Theoretische Studien Heidelberg Das HITS betreibt Grundlagenforschung in den Naturwissenschaften, der Mathematik und der Informatik. Die Forschungsfelder reichen dabei von der Molekularbiologie bis zur Astrophysik. Interdisziplinäres Zentrum für wissenschaftliches Rechnen (IWR) Heidelberg Entwicklung von mathematischen und rechnerischen Methoden für Naturwissenschaft, Ingenieurwesen und Geisteswissenschaften.

 

Deutschland ist mit der angestrebten Forschungs- und Entwicklungsquote von 3,5% gemessen an der jährlichen Wirtschaftsleistung bereits auf einem sehr guten Weg, um weiterhin im Spitzenfeld der innovativen Länder eine entscheidende Rolle zu spielen. Das Institut der Deutschen Wirtschaft mahnt jedoch unter Berufung auf eine Studie von Erdmann et. al^[16], dass eine Erhöhung der Ausgaben für Forschung und Entwicklung allein zu keiner Steigerung der Innovationsleistung führt, sondern das dies von einer Vielzahl an Faktoren abhängt:

 

„Wie erfolgreich eine Volkswirtschaft im internationalen Innovationswettbewerb abschneidet, hängt von mehreren sich ergänzenden, sich gegebenenfalls aber auch wechselseitig limitierenden Faktoren ab. So führt eine gesamtwirtschaftliche Erhöhung der Forschungs- und Entwicklungsaufwendungen allein zu keiner zusätzlichen Innovationsleistung, wenn sich keine adäquat qualifizierten Arbeitskräfte für die zusätzlichen Ressourcen finden lassen. Auch führt die bloße Erteilung zusätzlicher Patente nicht zwangsläufig zu mehr Innovationen, wenn die Umsetzung technischer Eigentums- und Schutzrechte durch eine restriktive Reglementierung der potenziellen Absatzmärkte oder das Fehlen von Kapital zur Finanzierung der notwendigen Innovationsaufwendungen verhindert wird.“^[17]

 

Eine Steigerung der Innovationskraft kann nicht ohne eine parallellaufende Politik zur Sicherung qualifizierter MINT-Arbeitskräfte vonstattengehen. „Ein höheres Angebot an Arbeitskräften mit innovationsrelevanten Qualifikationen führt über zusätzliche Innovationen zu einer steigenden Totalen Faktorproduktivität (Dakhli/De Clercq, 2004; Aghion/Howitt, 2006)“.^[18] Hierfür ist es notwendig, sowohl die Zahl der Studierenden in diesen Fächern zu erhöhen als auch die Absolventen und Absolventinnen durch ausreichende Förderung und ideelle sowie finanzielle Unterstützung zu den Innovatoren und Innovatorinnen von morgen werden zu lassen.

 

Die Zukunft der Mathematik

Der Nationale Forschungsrat der USA (National Research Council, NRC) hat sich in einer Studie zur Mathematik der Zukunft intensiv mit der Frage auseinandergesetzt, wie mathematische Forschung aussehen sollte, um den Anforderungen dieses Jahrzehnts gewachsen zu sein. Als einen der grundlegenden Aspekte für eine gewinnbringende und zielorientierte Forschung sehen sie eine Ausweitung und Erweiterung des Verständnisses von Mathematik. Dies bezieht sich zum einen auf die konkreten Anwendungsbereiche von Forschungsergebnissen, aber auch auf die Forderung nach einer stärkeren Interdisziplinarität mathematischer Forschung. Der NCR betrachtet dies als grundlegende Veränderung zur Sicherstellung wirtschaftlichen Wachstums, nationaler Wettbewerbsfähigkeit und nationaler Sicherheit.

 

“Mathematical sciences work is becoming an increasingly integral and essential component of a growing array of areas of investigation in biology, medicine, social sciences, business, advanced design, climate, finance, advanced materials, and many more. This work involves the integration of mathematics, statistics, and computation in the broadest sense and the interplay of these areas with areas of potential application. All of these activities are crucial to economic growth, national competitiveness, and national security, and this fact should inform both the nature and scale of funding for the mathematical sciences as a whole.” ^[19]

 

Der NRC mahnt, dass vielen Mathematiker*innen nicht ausreichend bewusst ist, welche sich kontinuierlich erweiternde Rolle ihr Fachbereich einnimmt. Um bereits den Studierenden der Mathematik ein Bewusstsein dafür zu vermitteln, wie unabdingbar Mathematik für fast alle Bereiche unseres täglichen Lebens und insbesondere in der Forschung zahlloser Disziplinen ist, sollte sich diese Entwicklung auch bereits im Curriculum der betreffenden Studiengänge wiederfinden.^[20]

Durch die stark gestiegene Bedeutung der Mathematik für die Fragestellungen, Märkte, Entwicklungen und Veränderungen von morgen besteht für die Mathematik nun die historische Chance, sich sowohl in der Forschungslandschaft, in der gesellschaftlichen Wahrnehmung als auch im Hinblick auf Ihre volkswirtschaftliche Bedeutung neu zu positionieren. Die Mathematik sollte ihre Stärken in der Grundlagenforschung beibehalten, sich jedoch gleichermaßen auf ihre Rolle als Schlüsseltechnologie fokussieren und in diesem Zusammenhang interdisziplinär und anwendungsorientiert forschen und arbeiten. Das Committee on the Mathematical Sciences in 2025 hat festgestellt, dass die Grenzen zwischen den verschiedensten Teilbereichen der Mathematik zunehmend verschwimmen und dass dieser Effekt auch zwischen der Mathematik und anderen Forschungsdisziplinen der Fall ist. Mathematische Forschung wird somit nicht mehr nur durch interdisziplinäre Projekte bereichert, sondern auch dadurch, dass die Mathematik zu einem essenziellen Teilbereich vieler weiterer Disziplinen geworden ist.^[21] Mathematik wird somit zunehmend zu einem transdisziplinären Wissenschaftsfeld. Darüber hinaus rückt, insbesondere durch die Anknüpfung an andere Disziplinen, der Anwendungsbezug mathematischer Forschung stärker in den Vordergrund.

Mathematische Bereiche ^[22]

Das Komitee ruft folglich dazu auf, die Mathematik breiter zu fassen und alle mathematischen Bereiche als Ganzes zu verstehen (entgegen der häufig gängigen Praxis sich vor allem über Unterdisziplinen zu definieren). Die Trennung in Grundlagenmathematik und die angewandte Mathematik erweist sich in Anbetracht der Realität und der Anforderungen der Zukunft als überholt. ^[23]

 

NRC-Vorschläge zur Zukunft der Mathematik Um die Mathematik im 21. Jahrhundert als Schlüsseltechnologie zu etablieren, gibt der NRC eine Reihe von Vorschlägen für eine gelungene Etablierung als Dreh- und Angelpunkt zukunftsgerichteter Forschung:[24] Forscher*innen sollten sich nicht nur auf ihre persönlichen Schwerpunkte konzentrieren, sondern die Mathematik als Ganzes im Blick behalten und eine breite Ausbildung anstreben. Hierfür muss ein Bewusstsein für die Bedeutung der Mathematik weit über Fachgrenzen hinaus bestehen. Die Ausbildung sollte dementsprechend angepasst werden. Mathematiker*innen sollten Wert auf einen zielgerichteten und häufigen Austausch mit Forschern und Forscherinnen anderer Disziplinen legen. Mathematische Institute sollen sich hierfür als Anknüpfungspunkte für transdisziplinäre Projekte verstehen. Auf diese Weise ist es möglich ein Netzwerk für Kollaborationen weit über Fachgrenzen hinaus zu bilden. Mathematiker*innen sollten Erfahrungen im Bereich des „Computing“ haben. Der Einfluss von Mathematik und der Wert mathematischer Forschung für Gesellschaft und Wirtschaft sollte stärker in den Vordergrund gerückt werden, um die Sichtbarkeit und damit auch die Förderung mathematischer Forschung zu forcieren.

 

Fazit: (Kernthesen zum Mitnehmen) Der Wert mathematischer Forschung für Gesellschaft und Entwicklung ist nicht messbar und die Bedeutung einzelner mathematischer Erkenntnisse ist häufig losgelöst vom Zeitpunkt der Findung. Die Mathematik der Zukunft sollte interdisziplinär sein und die Grundlagenforschung als auch die Anwendungsorientierung gleichermaßen im Blick behalten. Mit einer jährlichen Forschungs- und Entwicklungsquote von 3,17 % (2019) gemessen am jährlichen Bruttoinlandsprodukt befindet sich Deutschland im europäischen Spitzenfeld. Die Steigerung der Innovationskraft eines Landes ist ein Zusammenspiel verschiedenster Faktoren. Die alleinige Steigerung der Ausgaben für Forschung und Entwicklung reicht hierbei nicht aus, sondern weitere Faktoren (z.B. Sicherung von Fachkräften, Patentanmeldungen) müssen ebenfalls berücksichtigt werden.

 

 Ein Gastbeitrag von Ilka Agricola und Verena Reiter

Aktualisiert 2023.

---

^[1] Bundesministerium für Bildung und Forschung. Künstliche Intelligenz macht personalisierte Schlaganfall-Therapie möglich. 20.05.2020, https://tinyurl.com/29dhutyz

^[2] Heike Kampe. Die Macht der Zahlen. Otto von Guericke Universität Magdeburg, 21.08.2019, https://tinyurl.com/yc6w42sm

^[3] Bernd Müller. Große Schritte für kleine Geschäfte. Bild der Wissenschaft plus, Sonderpublikation in Zusammenarbeit mit dem Fraunhofer ITWM, 07/2018, pp. 20-21.

^[4] Die US-amerikanische National Academy of Sciences warnt in diesem Kontext: “Support for basic science is always fragile, and this may be especially true of the core mathematical sciences. In order for the whole mathematical sciences enterprise to flourish long term, the core must flourish. This requires investment by universities and by the government in the core of the subject. These investments are repaid not immediately and directly in applications but rather over the long term as the subject grows and retains its vitality. From this ever-increasing store of fundamental theoretical knowledge many innovative future applications will be drawn.” National Research Council 2013. The Mathematical Sciences in 2025. The National Academies Press, 2013, p.2.

^[5] Deutsche Forschungsgemeinschaft. Jahresbericht 2020. Aufgaben und Ergebnisse. Deutsche Forschungsgemeinschaft e.V., p. 50.

^[6]  Bundesministerium für Bildung und Forschung. Daten und Fakten zum deutschen Forschungs- und Innovationssystem. Bundesbericht Forschung und Innovation 2020. 2020, p. 7.

^[7] Mathematical Research Data Initiative (MaRDI), https://www.dfg.de/download/pdf/foerderung/programme/nfdi/nfdi_konferenz_2020/mardi_abstract.pdf.  “Mission.” Mathematical Research Data Initiative, https://www.mardi4nfdi.de/about/mission Stand WIAS Berlin. Mathematische Forschungsdaten optimal nutzen. Deutsche Mathematiker Vereinigung, 08.07.2022, https://www.mathematik.de/Forschung/2907-mathematische-forschungsdaten-optimal-nutzen.

^[8] Bundesministerium für Bildung und Forschung. Bildung und Forschung in Zahlen 2021. 2021, p. 7.

^[9] European Commission. R&D expenditure in the EU at 2.3% of GDP in 2020. Eurostat, 29.11.2021, https://ec.europa.eu/eurostat/en/web/products-eurostat-news/-/DDN-20211129-2.

^[10] Bundesministerium für Bildung und Forschung. Daten und Fakten zum deutschen Forschungs- und Innovationssystem. Bundesbericht Forschung und Innovation 2020. 2020, p. 10.

^[11] Bundesministerium für Bildung und Forschung. Datenportal. Tab 1.1.5 (BuFI 5). Ausgaben des Bundes für Wissenschaft, Forschung und Entwicklung nach Förderbereichen und Förderschwerpunkten. https://www.datenportal.bmbf.de/portal/de/K1.html.

^[12] Heike Faßbender and Volker Mehrmann. Drittmitteleinwerbung. Jeder Antrag zählt. Mitteilungen der Deutschen Mathematiker-Vereinigung, 27 (3-4), 2020, pp. 156-157.

^[13] DFG. Jahresbericht 2022. Aufgaben und Ergebnisse. Deutsche Forschungsgemeinschaft e.V., 2023. p. 205. https://www.dfg.de/dfg_profil/ueber_die_dfg/jahresbericht/index.html.

^[14] Fachkollegium 312 (Mathematik) der DFG: https://www.dfg.de/dfg_profil/gremien/fachkollegien/liste/index.jsp?id=312.

^[15] DFG Fachkollegienreport 2020. Deutsche Forschungsgemeinschaft e.V., 2021.

^[16] Vera Erdmann, Oliver Koppel, Axel Plünnecke. Innovationsmonitor. Die Innovationskraft Deutschlands im internationalen Vergleich. Forschungsberichte aus dem Institut der deutschen Wirtschaft Köln, 79, 2012.

^[17] Christina Anger, Oliver Köppel und Axel Plünnecke. MINT-Frühjahrsreport 2017. MINT-Bildung: Wachstum für die Wirtschaft, Chancen für den Einzelnen. Gutachten für BDA, BDI, MINT Zukunft schaffen und Gesamtmetall. Institut der deutschen Wirtschaft, 2017, p. 10.

^[18] Ibid.

^[19] National Research Council 2013. The Mathematical Sciences in 2025. The National Academies Press, 2013, p. 2.

^[20] Ibid.

^[21] Ibid, p. 4.

^[22] National Research Council 2013. The Mathematical Sciences in 2025. The National Academies Press, 2013, p. 63.

^[23] Ibid., p. 5.

^[24] Ibid., pp. 3-4.

Um einen Kommentar zu verfassen, müssen Sie sich einloggen bzw. kurz als Gast registrieren.