Im aktuellen Heft der "Mitteilungen" (der Deutsche Mathematiker-Vereinigung, Heft 1/ 2024) empfehlen wir diesen Artikel zum Farbengleichheitsmuster:
Farbengleichheitsmuster sind Muster wo alle sechs Farben auf dem Würfel genau gleich arrangiert sind. Wir fangen an mit einem 2×2×2 Würfel wo zusätzlich ein Eckstück einmal verdreht ist. Von dieser Ausgangsposition gibt es 21 verschiedene Gleichheitsmuster, die eine Reihe von interessanten Symmetrien aufweisen. Diese Eckmuster können dann kombiniert werden mit den anderen Stücken auf 3×3×3 Würfeln, wobei Symmetrien wieder eine wichtige Rolle spielen.
Es sind jetzt 50 Jahre seit der Rubik-Würfel zuerst erschien. In letzten Jahren hat es erneutes Interesse gegeben, besonders mit der Entwicklung von zunehmend größeren Würfeln, jetzt erhältlich bis zu 21 × 21 × 21. Viele Enthusiasten fokussieren auf Geschwindigkeitswettbewerbe, oder auf besondere Muster die konstruiert werden können, manche recht elegant. Mathematiker sind typischerweise mehr interessiert an Aspekten wie die zugrundeliegende gruppentheoretische Struktur, oder die maximale Zahl von Zügen um eine willkürliche Anordnung zu lösen, auf dem Original [3] und auch größeren Würfeln [4].
Als Mathematiker und Würfel-Enthusiast bekam ich interessiert an besonderen Mustern die auf den ersten Blick recht abstrakt erscheinen, aber eine sehr präzise mathematische Definition haben. Wir definieren ein Farbengleichheitsmuster als eins wo all sechs Farben genau gleich verteilt sind. Das heißt, wenn man zwei identisch arrangierte Würfel hätte, könnte man sie relativ zueinander rotieren sodass eine Farbe auf dem ersten Würfel und eine beliebige andere Farbe auf dem zweiten Würfel in allen Positionen übereinstimmen.
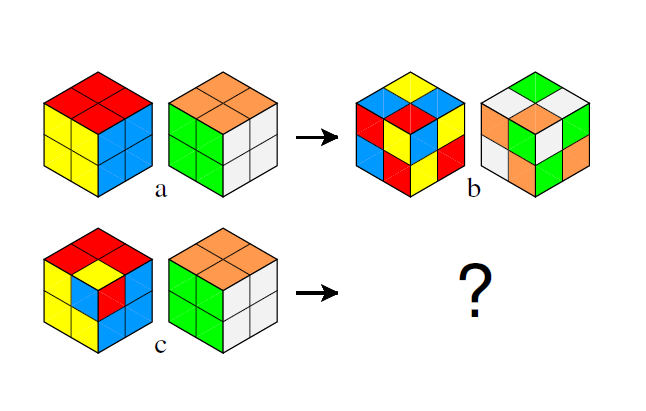
Abbildung 1
Abbildung 1. Tafel (a) zeigt die Standardanordnung; (b) zeigt ein komplizierteres Farbengleichheitsmuster, das daraus konstruiert werden kann. Tafel (c) zeigt die verdrehte Konfiguration; die Frage ist dann was für Gleichheitsmuster daraus konstruiert werden können. Abbildung 1 zeigt zwei Beispiele auf dem nur aus Eckstücken bestehenden 2 × 2 × 2 Würfel.
Abbildung 1a zeigt die standard gelöste Anordnung, die selbst ein Gleichheitsmuster ist, allerdings ein recht einfaches. Abbildung 1b zeigt ein komplizierteres Gleichheitsmuster, das aus der Standardanordnung konstruiert werden kann. Insgesamt gibt es 12 solche Muster auf dem 2×2×2 Würfel.
Als Nächstes betrachten wir Abbildung 1c, wo eine Ecke um eine Drehung im Uhrzeigersinn rotiert ist. Es gilt zuerst zu beachten das diese Anordnung nicht erreicht werden kann durch irgendeine legitime Folge von Zügen anfangend von Abbildung 1a. Der Würfel hat die bekannte Eigenschaft das die ersten sieben Ecken beliebig rotiert werden können, aber die Orientierung der letzten Ecke ist dann fixiert, ohne weitere Auswahl möglich [1]. Nehmen wir jedoch an, dass wir dem Würfel eine gewisse Gewalt antun, und wir zwingen eine Ecke verdreht zu sein wie in Abbildung 1c. Besonders wenn der Würfel ein bisschen lose ist, ist so eine Verdrehung meistens sehr leicht zu erreichen. Die Frage stellt sich dann, was für Farbengleichheitsmuster können aus dieser Startposition konstruiert werden? Und gerade weil Abbildungen 1a und 1c unter normal erlaubten Zügen nicht kompatibel sind, werden Muster die aus Abbildung 1c entstehen zwangsweise anders sein als die vorherigen 12 Muster.
Nun, es stellt sich heraus das selbst eine Startposition so asymmetrisch und geradezu hässlich wie Abbildung 1c etliche sehr elegante Gleichheitsmuster ergibt, mit interessanten und unerwarteten Vergleichen zwischen verschiedenen Mustern, in manchen Hinsichten sogar mehr noch als die vorherigen 12 Muster. Meine Hoffnung ist das diese Ergebnisse nicht nur unterhaltsam sind, sondern auch nützlich sein könnten um über verschiedene Aspekte von Symmetrien drei-dimensionaler
Muster zu unterrichten.
Den gesamten Artikel lesen Sie bei de Gruyter.
Der Autor Rainer Hollerbach ist Professor für Mathematik an der University of Leeds. Seine Fachgebiete sind Strömungen und Magnetfelder in astrophysikalischen Objekten.
Literatur
[1] C. Bandelow, Inside Rubik’s Cube and Beyond. Birkhäuser, 1982.
[2] J. Chen, Group Theory and the Rubik’s Cube (Lecture Notes), 2004. tinyurl.com/Chen-cube
[3] T. Rokicki, H. Kociemba, M. Davidson, J. Dethridge, The diameter of the Rubik’s Cube group
is twenty. SIAM Review 56, 645-670, 2014.
[4] E.D. Demaine, M.L. Demaine, S. Eisenstat, A. Lubiw, A. Winslow, Algorithms for solving
Rubik’s Cubes. European Symp. on Algorithms, 689-700, 2011.
dspace.mit.edu/handle/1721.1/73771
[5] R. Hollerbach, Colour equality patterns on Rubik’s Cubes. Mathematics Today 59, 115-117,
2023. eprints.whiterose.ac.uk/199822/
Prof. Dr. Rainer Hollerbach
School of Mathematics, University of Leeds
Woodhouse Lane, Leeds LS2 9JT, England
Diese E-Mail-Adresse ist vor Spambots geschützt! Zur Anzeige muss JavaScript eingeschaltet sein!