Ein Mädchen mit übersinnlichen Fähigkeiten, ein unbekanntes Genie und ein mathematischer Beweis, der jahrelang unentdeckt in den Tiefen des World Wide Web verharrte: Dies ist die Geschichte einer neuen unteren Schranke für Superpermutationen; und die sensationelle Geschichte ihrer Entdeckung.
Animés: Was für viele Menschen ein eigentümlicher Zeitvertreib für Sonderlinge ist, ist für manch anderen eine fantastische Welt voller Action, fesselnder Stories und liebenswürdiger Figuren. Die japanischen Zeichentrickserien und –Filme begeistern seit Jahren junge und ältere Zuschauer; sie handeln von Abenteuern, vom Erwachsenwerden, von Liebe und Zärtlichkeit und von Schmerz, von alltäglichen und von übernatürlichen; mal sind die Geschichten lustig, mal traurig, mal geistreich und mal ganz banal.
Haruhi Suzumiya: I'm Haruhi Suzumiya, from East Junior High. First off, I'm not interested in ordinary people. But, if any of you are aliens, time-travelers, or espers, please come see me. That is all!
Kyon: [Thinking] Is that supposed to be funny?
Die Serie Die Melancholie der Haruhi Suzumiya ist ein solcher Animé; sie handelt von der exzentrischen Schülerin Haruhi Suzumiya, einem Mädchen mit der Fähigkeit, die Realität nach ihren Wünschen zu verändern und ihrem sarkastisch-apathischen Mitschüler Kyon, der zu Beginn der Serie skeptisch gegenüber allem Übernatürlichen ist, aber gegen Ende zu Haruhi eine freundschaftliche Beziehung aufbaut. Zusammen mit der schüchternen Yuki und dem mysteriösen Itsuki gründen sie den Schulclub SOS Brigade, nichtsahnend, dass sie dabei von einer mächtigen Organisation beobachtet werden.
 Artwork zur Animé-Serie "Die Melancholie der Haruhi Suzumiya".
Artwork zur Animé-Serie "Die Melancholie der Haruhi Suzumiya".
"Each person has his or her own way of having fun."
-Itsuki Koizumi
Die Melancholie der Haruhi Suzumiya fand seit ihrer Erstaustrahlung weltweit Zuspruch: Es gibt Fantreffen, Merchandising, und in Diskussionsforen tauschen sich Fans und Liebhaber der Serie online über einzelne Aspekte des Animés und Folgen aus. Und aus genau einem solchen Diskussionsforum stammt die Lösung zu einem seit langem offenen mathematischen Problem. Worum geht es dabei?
Haruhi: ... After all, our goal each year should be to increase the NUMBER of goals we set for ourselves!
Bei der japanischen Erstaustrahlung wurde die erste Staffel von die Melancholie der Haruhi Suzumiya in nicht chronologischer Reihenfolge gesendet. Am Ende einer jeden Folge wurden zwei Vorschläge gemacht, wie die Serie fortzuführen sei: Ein Vorschlag kam dabei von Kyon, der andere von Haruhi. Die Reihenfolge, in der man die einzelnen Folgen anschaut, nimmt dabei Einfluss auf den Inhalt und das Gesamterlebnis der Staffel- welches die beste Reihenfolge ist, ist daher Gegenstand zahlreicher Diskussionen.
Vor diesem Hintergrund wurde im Jahr 2011 von einem User der bekannten Internetplattform 4chan die Frage gestellt, auf welche Art man die Episoden der ersten Staffel der Serie sehen muss, um jede denkbare Kombination an Folgen mindestens einmal gesehen zu haben. Um diese Frage entstand schnell eine lange Diskussion unter den Usern.
 Teile der Diskussion zum Beitrag.
Teile der Diskussion zum Beitrag.
Was dabei niemand bemerkte: Mit dieser Frage diskutierten die User ein bis dato offenes Problem der Kombinatorik, das Problem der Superpermutationen.
"Problems that cannot be solved do not exist in this world."
-Yuki Nagato
Gegeben sei eine Menge \(M\) bestehend aus \(n\) Elementen, zum Beispiel die Menge \(M= \{1,2,3\}\) mit drei Elementen oder die Menge der Episoden der ersten Staffel der Melancholie der Haruhi Suzumiya, bestehend aus \(n=14\) Episoden. Ordnet man die Elemente von \(M\) in einer bestimmten Reihenfolge an, spricht man von einer Permutation dieser Menge. Die Menge \(\{1,2,3\}\) lässt sechs mögliche Permutationen zu, nämlich \((123)\), \((231)\), \((312)\), \((132)\), \((321)\), und \((213)\), bei der ersten Staffel der Melancholie der Haruhi Suzumiya sind es hingegen \(14!=14 \cdot 13 \cdot … \cdot 3 \cdot 2 \cdot 1\) (lies: \(14\) Fakultät) Permutationen, also rund 87 Milliarden. Wie oben erwähnt, sorgt dabei jede Permutation für ein anderes Gesamterlebnis der Serie.
Man ist nun daran interessiert, eine Liste mit Einträgen von Elementen aus M zu erstellen, die folgende Eigenschaften hat:
(i) In der Liste kommt jede Permutation von M mindestens einmal vor.
(ii) Die Länge dieser Liste ist minimal.
Eine solche Liste heißt Superpermutation der Menge \(M\). Sei zum Beispiel \(M= \{1,2,3\}\). Eine Liste von Elementen aus \(M\), in der jede Permutation von \(M\) mindestens einmal vorkommt, könnte man beispielsweise dadurch erhalten, dass man die Permutationen von \(\{1,2,3\}\) hintereinanderschreibt, also\begin{align*}L_0=(123231312132321213).\end{align*}
Diese Liste ist aber augenscheinlich nicht die kürzeste ihrer Art; die Muster \((2323)\) am Anfang und \((2121)\) am Ende etwa sind redundant; die reduzierte Liste \begin{align*}L_1=(12313121323213)\end{align*}
erfüllt die Forderung (i) daher ebenfalls. Entfernt man sukzessive mehrfach vorkommende Einträge, gelangt man schließlich zur Liste \begin{align*}L_3=(1231213213).\end{align*}
Da die Permutation \((213)\) bereits in der Mitte vorkommt, kann man auf die \(3\) am Ende von \(L_3\) verzichten und gelangt somit zur Liste \begin{align*}L_4=(123121321).\end{align*}
Man kann zeigen, dass es keine kürzere derartige Liste geben kann; \(L_4\) ist damit eine Superpermutation der Menge \(\{1,2,3\}\).
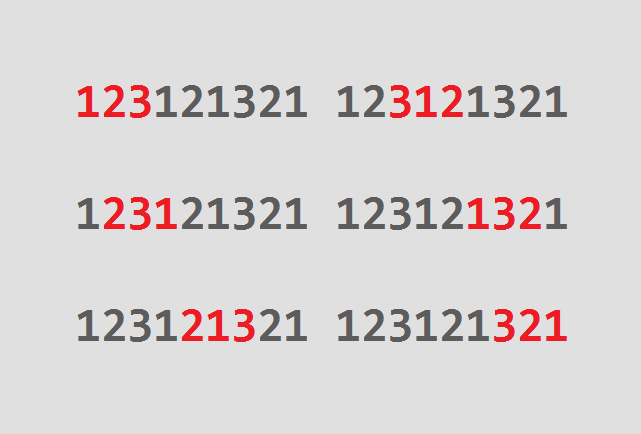 Eine Superpermutation der Menge \(\{1,2,3\}\): Jede mögliche Permutation kommt mindestens einmal vor.
Eine Superpermutation der Menge \(\{1,2,3\}\): Jede mögliche Permutation kommt mindestens einmal vor.
Wenn man die Episoden der Melancholie der Haruhi Suzumiya anhand einer Superpermutation sieht, bedeutet das also nichts anderes, als dass man die erste Staffel der Serie in jeder erdenklicher Reihenfolge gesehen hat- und das in kürzest möglicher Zeit.
Die Länge von Superpermutationen ist Gegenstand aktueller mathematischer Forschung. Wie bei vielen anderen Problemen in der Kombinatorik ist es auch beim Problem der Superpermutationen aufgrund der enormen Anzahl Kombinationen im Allgemeinen nicht möglich, ihre genauen Längen anzugeben. Daher ist es bereits ein Fortschritt, diese Zahl anzunähern: Je höher die untere Grenze und je niedriger die obere Grenze, desto besser lässt sich das genaue Ergebnis abschätzen.
Haruhi: And just what gives you the right to ask me a question like that? I don't know about anything you've heard. Whatever. You wanna believe it? It's probably true.
Um den Beitrag zum Problem der Superpermutationen der Serie auf 4chan entbrannte schnell eine seitenlange Diskussion. Viele User teilten ihre Lösungsvorschläge und Anregungen mit, während andere die Sinnhaftigkeit des Problems und ihrer Lösung infrage stellten. Doch anders als der Mathematik-Community, die sich über Jahre an dem Problem die Zähne ausgebissen hatte, gelang einem 4chan-User das Unvorstellbare: Im Beitrag Nr. 3751197 gab der anonyme Benutzer in einem groben Beweis eine neue untere Schranke für die Länge von Superpermutationen an- und verbesserte damit die bisherige untere Schranke um ein Vielfaches!
"Time never comes back once it’s gone."
-Haruhi Suzumiya
Obwohl er damit ein offenes mathematisches Problem löste, gerieten die Erkenntnisse des unbekannten Genies daraufhin für lange Zeit in Vergessenheit. Sieben Jahre lang blieb das Ergebnis unentdeckt, zu weit schien ein Diskussionsforum über Animès von der mathematischen Fachöffentlichkeit entfernt. Dies änderte sich erst im Oktober des Jahres 2018: Der Mathematiker und Blogger Robin Houston stieß durch Zufall auf den Beitrag und erkannte augenblicklich die Tragweite seiner Entdeckung.
A curious situation. The best known lower bound for the minimal length of superpermutations was proved by an anonymous user of a wiki mainly devoted to anime. https://t.co/z3wVAcUJl1
— Robin Houston (@robinhouston) October 23, 2018
Der in Großbritannien arbeitende Houston veröffentlichte daraufhin seine Entdeckung beim Microbloggingdienst Twitter; die Resonanz auf den Tweet war beachtlich: Sein Beitrag wurde wurde mehr als 4000 Mal aufgegriffen und fand weltweit Zuspruch, sowohl unter Laien, als auch unter Fachleuten. Expert_innen für Kombinatorik (unter anderem Housten selbst) überprüften unterdessen den Beweis des anonymen Users und befanden ihn für korrekt- Die Sensation war perfekt.
"Dreams start by believing."
-Haruhi Suzumiya
Dieses Zustandekommen eines mathematischen Satzes ist höchstwahrscheinlich das erste seiner Art. Dass ein mathematischer Satz von einem Laien bewiesen wurde ist nichts Neues: Beispielsweise entdeckte niemand geringeres als Napoleon Bonaparte einen interessanten Zusammenhang in der ebenen Geometrie, und Aubrey de Gray, der sich um die Lösung des Problems der chromatischen Zahl der Ebene verdient gemacht hat, ist eigentlich Biologe.
Ein mathematischer Beweis allerdings, der über Jahre hinweg unentdeckt geblieben ist, geführt von einem Laien, der sich des Umstandes nicht bewusst gewesen ist, in die Annnalen der Kombinatorik einzugehen, veröffentlicht in einem Animé-Forum und nach sieben Jahren durch Zufall wiederentdeckt ist nichts weniger als eine Geschichte, die vermutlich auf ewig ihresgleichen suchen wird.
Houston und andere Fachleute planen indes die Veröffentlichung eines Papers über die neue untere Schranke von Superpermutationen, in dem die Ergebnisse aus dem 4chan-Beitrag mathematisch präzise dargelegt werden sollen- selbstverständlich wird der anonyme User dabei als Co-Autor und sein 4chan-Beitrag als Quelle erwähnt; seine wahre Identität bleibt aber bis heute unbekannt.
Konrad Krug



