Vor einigen Tagen haben Joel Anthony Haddley und Stephen Worsley, Dozenten an der Universität Liverpool, mit einer Veröffentlichung im Archiv die Medienwelt heiß gemacht auf Mathematik. Inhalt: Eine angeblich neue Art, Pizza zu zerschneiden, und zwar so, dass jeder ein Teil derselben Form und Größe auf den Teller bekommt. Anders ausgedrückt, stellt die Idee von Haddley und Worsley einen Weg dar, Kreise mit einer einzigen Sorte Fliesen zu parkettieren. Die Grundfrage, die Geometer hier seit Jahrzehnten umtreibt ist: Gibt es eine Kachelung des Kreises mit einem einzigen Typ Fliesen, so dass genau eine Fliese den Mittelpunkt enthält?
Tatsächlich ist das eine offene Frage, die sich offenbar nicht leicht beantworten lässt. Kachelungen, bei denen der Mittelpunkt in jeder Kopie der Kachel liegt, kennt jeder Pizzabäcker: Man schneidet den Kreis einfach mit n Geraden, die sich im Mittelpunkt treffen und im Winkel 2pi/n stehen:
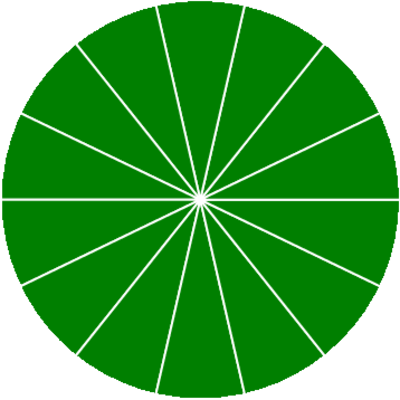
Kachelungen, bei denen genau eine Kachel den Mittelpunkt enthält, kennt dagegen niemand. Für das "gerechte" Teilen der Pizza brauchen die Schnitte aber natürlich nicht gerade zu sein, im Prinzip ist fast jede Kurve möglich:

Hier ist ein Stück dunkelgrün hervorgehoben. Man beachte, dass die Stücke beliebig "lang" und schmal gemacht werden können! Besonders hübsch wird die Teilung, wenn man Kreisbögen mit demselben Radius wie die Pizza wählt. Für 2pi/6 liegen die Ecken dann nämlich auf einem gleichseitigen Dreieck:

Unterteilt man das Dreieck nochmal gleichmäßig weiter mit Kreisbögen, dann kann man das ganze Dreieck spiegeln und so neue Parkettierungen des Kreises erzeugen: Wenn man die Kurven richtig wählt (zum Beispiel auf einfache Kreisbögen zurückgreift), dann lassen sich die Stücke obendrein mit geraden Schnitten halbieren, wodurch man weitere hübsche Parkettierungen des Kreises mit einem Kacheltyp erzeugen kann - wobei hier die Kachel beim Parkettieren allerdings auch gespiegelt wird. Immerhin führt das zu Parkettierungen, bei denen nur noch die Hälfte der Kacheln den Mittelpunkt berühren:
Wenn man die Kurven richtig wählt (zum Beispiel auf einfache Kreisbögen zurückgreift), dann lassen sich die Stücke obendrein mit geraden Schnitten halbieren, wodurch man weitere hübsche Parkettierungen des Kreises mit einem Kacheltyp erzeugen kann - wobei hier die Kachel beim Parkettieren allerdings auch gespiegelt wird. Immerhin führt das zu Parkettierungen, bei denen nur noch die Hälfte der Kacheln den Mittelpunkt berühren:

All diese Parkettierungen sind lange bekannt, und man erkennt unschwer, dass sie sich unendlich variieren lassen. Auch Haddleys und Worsleys Entdeckung sind im Prinzip nur eine Variation dieser bekannten Parkettierungen: Statt mit Kreisbögen teilen sie die Pizza mit einer Kurve, die sich aus eine Serie von Kreisbögen zusammensetzt. Die Verbindungspunkte liegen dabei auf einem Ausschnitt eines regelmäßigen m-Ecks, wobei das m ungerade ist. Für m=5 sieht das so aus:

Weil die "Halbmonde" symmetrisch sind, kann man sie nochmal in der Mitte durchschneiden, und genau das tun Haddley und Worsley. Für höhere m werden die Stücke dann immer schmaler, aber es tut sich nichts wesentlich Neues mehr:  Haddley und Worsley stellen in ihrer Arbeit noch eine andere Teilung vor, die nach ähnlichem Prinzip erzeugt wird.
Haddley und Worsley stellen in ihrer Arbeit noch eine andere Teilung vor, die nach ähnlichem Prinzip erzeugt wird.
Doch es gibt noch viele andere interessante Arten, mathematisch Pizza aufzuteilen. Am coolsten finde ich diese Methode: Man schneidet die Pizza mit geraden Schnitten in n aufeinander folgend nummerierten Stücke, wobei n durch 4 teilbar und mindestens 8 sein muss und zwei aufeinanderfolgende Geraden den Winkel 2pi/n einschließen sollen: 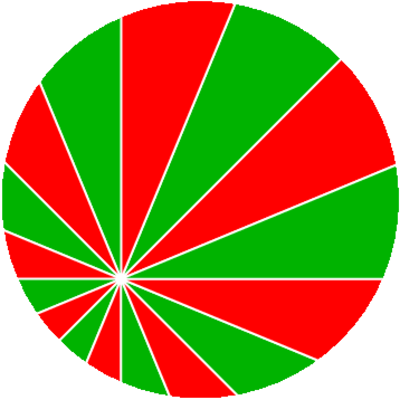 Dann ist - wie 1968 bewiesen wurde - die Gesamtfläche der Stücke mit geraden Nummern gleich der Gesamtfläche der Stücke mit ungeraden Nummern. Und bei dieser Unterteilung kann man sogar den Mittelpunkt in genau ein Stück legen!
Dann ist - wie 1968 bewiesen wurde - die Gesamtfläche der Stücke mit geraden Nummern gleich der Gesamtfläche der Stücke mit ungeraden Nummern. Und bei dieser Unterteilung kann man sogar den Mittelpunkt in genau ein Stück legen!
Andreas Loos



