Jeder kennt solche auch künstlerisch ansprechendenen Bilder von Fraktalen

Aber was stellen diese Bilder eigentlich dar?
Zur Erklärung dieser Bilder benötigt man
Komplexe Zahlen. Wer mit komplexen Zahlen nicht vertraut ist, sollte einfach nur wissen, daß komplexe Zahlen eine Möglichkeit bieten, Punkte der Ebene zu addieren und multiplizieren.
(Wen die mathematischen Details interessieren: jeder Punkt in der Ebene wird durch zwei Größen charakterisiert, nämlich den Radius, d.h. Abstand vom Nullpunkt, und den Winkel zwischen Radius und x-Achse. Die Multiplikation zweier als komplexer Zahlen aufgefaßter Punkte erfolgt dann durch Multiplikation der Radien und Addition der Winkel.
Und die Addition komplexer Zahlen ist die übliche Vektor-Addition.
Zum Beispiel ist der Punkt (0,1), auch als komplexe Zahl i bezeichnet, der Punkt mit Radius 1 und Winkel 90 Grad. Wenn ich i mit i multipliziere, multiplizieren sich die Radien und addieren sich die Winkel, ich erhalte also Radius 1 und Winkel 180 Grad. Dies entspricht dem Punkt (-1,0), also der komplexen Zahl -1.)
Wenn man eine Funktion f hat, kann man sich anschauen, wie sich eine komplexe Zahl z bei wiederholter Anwendung von f verhält, d.h. wir untersuchen die Folge z, f(z), f(f(z)), f(f(f(z))) usw.
Als ein besonders einfaches Beispiel betrachte man etwa die Funktion f(z)=z
2. Für einen komplexe Zahl z untersuchen wir also die Folge z, f(z)=z
2, f(f(z))=z
4, f(f(f(z)))=z
8 usw. Für z=1 etwa erhält man 1,1,1,1,..., für z=-1 erhält man -1,1,1,1,..., für z=i erhält man i,-1,1,1,...Wenn man aber zum Beispiel z=2 einsetzt erhält man die Folge 2,4,8,16,... die 'gegen Unendlich' geht. Und wenn man z=1/2 einsetzt, erhält man die Folge 1/2,1/4,1/8,1/16,... die gegen Null geht.
Man kann sich im Beispiel f(z)=z
2 leicht überlegen, daß, immer wenn man für z eine komplexe Zahl mit Radius größer 1 einsetzt, die Folge z, f(z), f(f(z)), f(f(f(z))),... gegen Unendlich geht. (Einfach, weil die Folge der Radien gegen Unendlich geht.)
Wenn man dagegen für z eine komplexe Zahl mit Radius höchstens 1 einsetzt, dann werden auch z
2,z
4,z
8,... wieder Radius höchstens 1 haben. Die Folge bleibt also im Inneren der Kreisfläche vom Radius 1 'gefangen'.
Allgemein bezeichnet man nun für ein Polynom f als
Gefangenenmenge die Menge der komplexen Zahlen z, für die die Folge z, f(z), f(f(z)), f(f(f(z))),... in einer Kreisfläche (von endlichem Radius) gefangen bleibt, und als
Fluchtmenge die Menge der komplexen Zahlen z, für die die Folge z, f(z), f(f(z)), f(f(f(z))),... gegen Unendlich geht.
Im Fall von f(z)=z
2 ist also die Gefangenmenge von f die Menge aller komplexen Zahlen mit Radius höchstens 1, und die Fluchtmenge von f ist die Menge aller komplexen Zahlen mit Radius größer 1.
Als
Julia-Menge von f bezeichnet man dann einfach den Rand der Gefangenenmenge.
Für f(z)=z
2 ist das einfach der Kreis vom Radius 1, also kein kompliziertes Bild. Es war aber schon in den 20er Jahren durch Arbeiten von Gaston Julia bekannt, das für andere Funktionen viel kompliziertere fraktale Mengen erhalten werden.
Die Arbeiten von Julia und Fatou waren unter Mathematikern durchaus gut bekannt. Große Popularität erlangten sie aber erst, als es 60 Jahre später durch den Einsatz von Computern möglich wurde, Julia-Mengen auch in graphisch anspruchsvoller Form darzustellen. Das Bild im Titel stellt z.B. die Julia-Menge von f(z)=z
5+0,70365...+0,2301...i dar. (Quelle:Wikipedia) Das Schwarzblaue ist die Fluchtmenge, das Bunte die Gefangenenmenge, die Julia-Menge ist der Rand des bunten Gebiets. (Von den Farben sollte man sich nicht verwirren lassen, sie dienen vor allem der graphischen Verschönerung.)
Die Möglichkeit von Computerexperimenten hat nicht nur zu schönen Bildern, sondern auch zur Aufdeckung vieler tiefliegender Zusammenhänge geführt, deren Beweise auch Entwicklungen in der Reinen Mathematik angestoßen haben. Ein aktuelles Resultat (2005) stammt z.B. von Xavier Buff und Arnaud Cheritat und besagt, daß es quadratische Polynome gibt, für die die Julia-Menge (also der RAND der Gefangenenmenge) positiven Flächeninhalt hat.
Viele Bilder von Julia-Mengen findet man auch im bekannten Buch
The Beauty of Fractals. Dort findet man auch folgendes Zitat des vor kurzem verstorbenen Mathematikers
Adrien Douady, nach dem das unten abgebildete Douady-Kaninchen benannt ist. (Quelle: Wolfram Mathworld; es handelt sich um die Julia-Menge von f(z)=z
2-0,123...+0,745...i)
Douady:
Ich muß sagen, jedesmal wenn ich 1980 meinen Freunden erzählt habe, daß ich gerade angefangen habe, mit J.H.Hubbard die Polynome vom Grad 2 in einer komplexen Variablen zu untersuchen (und genauer gesagt die Polynome der Form z --> z2+c), haben sie mich verständnislos angestarrt und gefragt: Glaubst du denn, du hast Aussicht, irgend etwas Neues zu entdecken? Aber gerade diese simple Familie von Polynomen ist es, die dafür verantwortlich ist jene Objekte zu erzeugen die so kompliziert sind - nicht chaotisch, sondern im Gegenteil: streng organisiert nach hochentwickelten kombinatorischen Gesetzen.
 Aber was stellen diese Bilder eigentlich dar?
Zur Erklärung dieser Bilder benötigt man Komplexe Zahlen. Wer mit komplexen Zahlen nicht vertraut ist, sollte einfach nur wissen, daß komplexe Zahlen eine Möglichkeit bieten, Punkte der Ebene zu addieren und multiplizieren.
(Wen die mathematischen Details interessieren: jeder Punkt in der Ebene wird durch zwei Größen charakterisiert, nämlich den Radius, d.h. Abstand vom Nullpunkt, und den Winkel zwischen Radius und x-Achse. Die Multiplikation zweier als komplexer Zahlen aufgefaßter Punkte erfolgt dann durch Multiplikation der Radien und Addition der Winkel.
Und die Addition komplexer Zahlen ist die übliche Vektor-Addition.
Zum Beispiel ist der Punkt (0,1), auch als komplexe Zahl i bezeichnet, der Punkt mit Radius 1 und Winkel 90 Grad. Wenn ich i mit i multipliziere, multiplizieren sich die Radien und addieren sich die Winkel, ich erhalte also Radius 1 und Winkel 180 Grad. Dies entspricht dem Punkt (-1,0), also der komplexen Zahl -1.)
Wenn man eine Funktion f hat, kann man sich anschauen, wie sich eine komplexe Zahl z bei wiederholter Anwendung von f verhält, d.h. wir untersuchen die Folge z, f(z), f(f(z)), f(f(f(z))) usw.
Als ein besonders einfaches Beispiel betrachte man etwa die Funktion f(z)=z2. Für einen komplexe Zahl z untersuchen wir also die Folge z, f(z)=z2, f(f(z))=z4, f(f(f(z)))=z8 usw. Für z=1 etwa erhält man 1,1,1,1,..., für z=-1 erhält man -1,1,1,1,..., für z=i erhält man i,-1,1,1,...Wenn man aber zum Beispiel z=2 einsetzt erhält man die Folge 2,4,8,16,... die 'gegen Unendlich' geht. Und wenn man z=1/2 einsetzt, erhält man die Folge 1/2,1/4,1/8,1/16,... die gegen Null geht.
Man kann sich im Beispiel f(z)=z2 leicht überlegen, daß, immer wenn man für z eine komplexe Zahl mit Radius größer 1 einsetzt, die Folge z, f(z), f(f(z)), f(f(f(z))),... gegen Unendlich geht. (Einfach, weil die Folge der Radien gegen Unendlich geht.)
Wenn man dagegen für z eine komplexe Zahl mit Radius höchstens 1 einsetzt, dann werden auch z2,z4,z8,... wieder Radius höchstens 1 haben. Die Folge bleibt also im Inneren der Kreisfläche vom Radius 1 'gefangen'.
Allgemein bezeichnet man nun für ein Polynom f als Gefangenenmenge die Menge der komplexen Zahlen z, für die die Folge z, f(z), f(f(z)), f(f(f(z))),... in einer Kreisfläche (von endlichem Radius) gefangen bleibt, und als Fluchtmenge die Menge der komplexen Zahlen z, für die die Folge z, f(z), f(f(z)), f(f(f(z))),... gegen Unendlich geht.
Im Fall von f(z)=z2 ist also die Gefangenmenge von f die Menge aller komplexen Zahlen mit Radius höchstens 1, und die Fluchtmenge von f ist die Menge aller komplexen Zahlen mit Radius größer 1.
Als Julia-Menge von f bezeichnet man dann einfach den Rand der Gefangenenmenge.
Für f(z)=z2 ist das einfach der Kreis vom Radius 1, also kein kompliziertes Bild. Es war aber schon in den 20er Jahren durch Arbeiten von Gaston Julia bekannt, das für andere Funktionen viel kompliziertere fraktale Mengen erhalten werden.
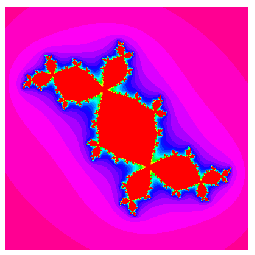
Die Arbeiten von Julia und Fatou waren unter Mathematikern durchaus gut bekannt. Große Popularität erlangten sie aber erst, als es 60 Jahre später durch den Einsatz von Computern möglich wurde, Julia-Mengen auch in graphisch anspruchsvoller Form darzustellen. Das Bild im Titel stellt z.B. die Julia-Menge von f(z)=z5+0,70365...+0,2301...i dar. (Quelle:Wikipedia) Das Schwarzblaue ist die Fluchtmenge, das Bunte die Gefangenenmenge, die Julia-Menge ist der Rand des bunten Gebiets. (Von den Farben sollte man sich nicht verwirren lassen, sie dienen vor allem der graphischen Verschönerung.)
Die Möglichkeit von Computerexperimenten hat nicht nur zu schönen Bildern, sondern auch zur Aufdeckung vieler tiefliegender Zusammenhänge geführt, deren Beweise auch Entwicklungen in der Reinen Mathematik angestoßen haben. Ein aktuelles Resultat (2005) stammt z.B. von Xavier Buff und Arnaud Cheritat und besagt, daß es quadratische Polynome gibt, für die die Julia-Menge (also der RAND der Gefangenenmenge) positiven Flächeninhalt hat.
Viele Bilder von Julia-Mengen findet man auch im bekannten Buch The Beauty of Fractals. Dort findet man auch folgendes Zitat des vor kurzem verstorbenen Mathematikers Adrien Douady, nach dem das unten abgebildete Douady-Kaninchen benannt ist. (Quelle: Wolfram Mathworld; es handelt sich um die Julia-Menge von f(z)=z2-0,123...+0,745...i)
Douady: Ich muß sagen, jedesmal wenn ich 1980 meinen Freunden erzählt habe, daß ich gerade angefangen habe, mit J.H.Hubbard die Polynome vom Grad 2 in einer komplexen Variablen zu untersuchen (und genauer gesagt die Polynome der Form z --> z2+c), haben sie mich verständnislos angestarrt und gefragt: Glaubst du denn, du hast Aussicht, irgend etwas Neues zu entdecken? Aber gerade diese simple Familie von Polynomen ist es, die dafür verantwortlich ist jene Objekte zu erzeugen die so kompliziert sind - nicht chaotisch, sondern im Gegenteil: streng organisiert nach hochentwickelten kombinatorischen Gesetzen.
Aber was stellen diese Bilder eigentlich dar?
Zur Erklärung dieser Bilder benötigt man Komplexe Zahlen. Wer mit komplexen Zahlen nicht vertraut ist, sollte einfach nur wissen, daß komplexe Zahlen eine Möglichkeit bieten, Punkte der Ebene zu addieren und multiplizieren.
(Wen die mathematischen Details interessieren: jeder Punkt in der Ebene wird durch zwei Größen charakterisiert, nämlich den Radius, d.h. Abstand vom Nullpunkt, und den Winkel zwischen Radius und x-Achse. Die Multiplikation zweier als komplexer Zahlen aufgefaßter Punkte erfolgt dann durch Multiplikation der Radien und Addition der Winkel.
Und die Addition komplexer Zahlen ist die übliche Vektor-Addition.
Zum Beispiel ist der Punkt (0,1), auch als komplexe Zahl i bezeichnet, der Punkt mit Radius 1 und Winkel 90 Grad. Wenn ich i mit i multipliziere, multiplizieren sich die Radien und addieren sich die Winkel, ich erhalte also Radius 1 und Winkel 180 Grad. Dies entspricht dem Punkt (-1,0), also der komplexen Zahl -1.)
Wenn man eine Funktion f hat, kann man sich anschauen, wie sich eine komplexe Zahl z bei wiederholter Anwendung von f verhält, d.h. wir untersuchen die Folge z, f(z), f(f(z)), f(f(f(z))) usw.
Als ein besonders einfaches Beispiel betrachte man etwa die Funktion f(z)=z2. Für einen komplexe Zahl z untersuchen wir also die Folge z, f(z)=z2, f(f(z))=z4, f(f(f(z)))=z8 usw. Für z=1 etwa erhält man 1,1,1,1,..., für z=-1 erhält man -1,1,1,1,..., für z=i erhält man i,-1,1,1,...Wenn man aber zum Beispiel z=2 einsetzt erhält man die Folge 2,4,8,16,... die 'gegen Unendlich' geht. Und wenn man z=1/2 einsetzt, erhält man die Folge 1/2,1/4,1/8,1/16,... die gegen Null geht.
Man kann sich im Beispiel f(z)=z2 leicht überlegen, daß, immer wenn man für z eine komplexe Zahl mit Radius größer 1 einsetzt, die Folge z, f(z), f(f(z)), f(f(f(z))),... gegen Unendlich geht. (Einfach, weil die Folge der Radien gegen Unendlich geht.)
Wenn man dagegen für z eine komplexe Zahl mit Radius höchstens 1 einsetzt, dann werden auch z2,z4,z8,... wieder Radius höchstens 1 haben. Die Folge bleibt also im Inneren der Kreisfläche vom Radius 1 'gefangen'.
Allgemein bezeichnet man nun für ein Polynom f als Gefangenenmenge die Menge der komplexen Zahlen z, für die die Folge z, f(z), f(f(z)), f(f(f(z))),... in einer Kreisfläche (von endlichem Radius) gefangen bleibt, und als Fluchtmenge die Menge der komplexen Zahlen z, für die die Folge z, f(z), f(f(z)), f(f(f(z))),... gegen Unendlich geht.
Im Fall von f(z)=z2 ist also die Gefangenmenge von f die Menge aller komplexen Zahlen mit Radius höchstens 1, und die Fluchtmenge von f ist die Menge aller komplexen Zahlen mit Radius größer 1.
Als Julia-Menge von f bezeichnet man dann einfach den Rand der Gefangenenmenge.
Für f(z)=z2 ist das einfach der Kreis vom Radius 1, also kein kompliziertes Bild. Es war aber schon in den 20er Jahren durch Arbeiten von Gaston Julia bekannt, das für andere Funktionen viel kompliziertere fraktale Mengen erhalten werden.
Die Arbeiten von Julia und Fatou waren unter Mathematikern durchaus gut bekannt. Große Popularität erlangten sie aber erst, als es 60 Jahre später durch den Einsatz von Computern möglich wurde, Julia-Mengen auch in graphisch anspruchsvoller Form darzustellen. Das Bild im Titel stellt z.B. die Julia-Menge von f(z)=z5+0,70365...+0,2301...i dar. (Quelle:Wikipedia) Das Schwarzblaue ist die Fluchtmenge, das Bunte die Gefangenenmenge, die Julia-Menge ist der Rand des bunten Gebiets. (Von den Farben sollte man sich nicht verwirren lassen, sie dienen vor allem der graphischen Verschönerung.)
Die Möglichkeit von Computerexperimenten hat nicht nur zu schönen Bildern, sondern auch zur Aufdeckung vieler tiefliegender Zusammenhänge geführt, deren Beweise auch Entwicklungen in der Reinen Mathematik angestoßen haben. Ein aktuelles Resultat (2005) stammt z.B. von Xavier Buff und Arnaud Cheritat und besagt, daß es quadratische Polynome gibt, für die die Julia-Menge (also der RAND der Gefangenenmenge) positiven Flächeninhalt hat.
Viele Bilder von Julia-Mengen findet man auch im bekannten Buch The Beauty of Fractals. Dort findet man auch folgendes Zitat des vor kurzem verstorbenen Mathematikers Adrien Douady, nach dem das unten abgebildete Douady-Kaninchen benannt ist. (Quelle: Wolfram Mathworld; es handelt sich um die Julia-Menge von f(z)=z2-0,123...+0,745...i)
Douady: Ich muß sagen, jedesmal wenn ich 1980 meinen Freunden erzählt habe, daß ich gerade angefangen habe, mit J.H.Hubbard die Polynome vom Grad 2 in einer komplexen Variablen zu untersuchen (und genauer gesagt die Polynome der Form z --> z2+c), haben sie mich verständnislos angestarrt und gefragt: Glaubst du denn, du hast Aussicht, irgend etwas Neues zu entdecken? Aber gerade diese simple Familie von Polynomen ist es, die dafür verantwortlich ist jene Objekte zu erzeugen die so kompliziert sind - nicht chaotisch, sondern im Gegenteil: streng organisiert nach hochentwickelten kombinatorischen Gesetzen.




