"Physics, Topology, Logic and Computation: A Rosetta Stone" ist der Titel eines letzte Woche erschienenen Überblicks-Artikels von John Baez und Mike Stay, in dem es um die Rolle der Kategorientheorie in den vier genannten Gebieten geht. In der Quantenfeldtheorie sind Feynman-Graphen eine bekannte grafische Darstellung von Wechselwirkungen. In den beiden aktuellen Theorie-Ansätzen zur Erklärung der Quantengravitation kommen Strukturen vor, die man zumindest formal als zweidimensionale Analoga von Feynman-Graphen ansehen kann: - in der Schleifenquantengravitation benutzt man Spinschaumflächenstücke, - in der Stringtheorie kommen Flächen durch die zeitliche Bewegung von Strings zustande. Der Artikel behandelt verschiedene mathematische Strukturen, die formal denselben Gesetzen gehorchen. Dies sind: - in der Physik Systeme (Funktionen im Hilbertraum) und Prozesse (Operatoren), die den Übergang zwischen verschiedenen Systemen beschreiben, - in der Logik Sätze und Beweise, die den Übergang zwischen verschiedenen Sätzen beschreiben, - in der Berechenbarkeitstheorie Daten und Programme, die den Übergang zwischen verschiedenen Daten beschreiben, - in der Topologie Mannigfaltigkeiten und Kobordismen zwischen Mannigfaltigkeiten. 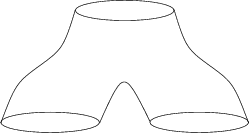Die ersten drei Punkte sind sicher klar, zum vierten Punkt eine kurze Erläuterung: Mannigfaltigkeiten sind bestimmte geometrische Gebilde, zum Beispiel (einer oder mehrere) Kreise. Ein Kobordismus zwischen zwei Mannigfaltigkeiten ist dann eine Mannigfaltigkeit (von um 1 höherer Dimension), deren Rand gerade aus den beiden Mannigfaltigkeiten besteht. Zum Beispiel ist ein Kreiszylinder ein Kobordismus zwischen zwei einzelnen Kreisen, während eine 'Hose' ein Kobordismus zwischen einem einzelnen Kreis und einem Paar von Kreisen ist. Als vereinheitlichende 'Metatheorie' für diese Strukturen hat man die Kategorientheorie. (Eine Kategorie besteht ganz abstrakt aus 'Objekten' und 'Morphismen' zwischen je zwei Objekten.) Das ist erst einmal nur eine gemeinsame Sprache, mit der man eben alle genannten Strukturen erfassen kann. Der Artikel beschäftigt sich hauptsächlich damit, kategorientheoretische Konstruktionen zu erklären, die sich in einzelnen der vier genannten Gebiete bereits als nützlich erwiesen haben. Die formale Übertragung der quantenfeldtheoretischen Methoden auf die Topologie ist seit 20 Jahren ein sehr aktives Forschungsgebiet, auch wenn wirklich überzeugende Anwendungen in der Topologie noch ausstehen. (Potentiell interessant wäre auf jeden Fall die, bisher nur in wenigen Spezialfällen bewiesene, Kashaev-Vermutung.) Entsprechend kann man formale Analogien der Toplogie dann also auch zur Logik und Theoretischen Informatik entwickeln. Ob dies nur deskriptiven Charakter hat oder auch tatsächlich etwa topologische Methoden zur Lösung von Problemen auf diesen Gebieten verwendet werden können, bleibt natürlich abzuwarten. In einem Artikel von Giraud werden zum Beispiel Beweise als dreidimensionale Kobordismen aufgefaßt, wobei dann schon Beweise recht simpler Formeln zu Bildern von komplizierten 3-dimensionalen Mannigfaltigkeiten zu führen scheinen. (Ich habe den Artikel nicht im Detail gelesen.) Analog kann man auch Programme als 3-Kategorien, und damit auch als 3-dimensionale Mannigfaltigkeiten auffassen. Auch wenn dies sicher kaum praktische Anwendungen haben dürfte, wäre es sicher interessant zu wissen welche (vermutlich sehr komplizierten) 3-Mannigfaltigkeiten etwa Linux oder Windows Vista entsprechen.

Um einen Kommentar zu verfassen, müssen Sie sich einloggen bzw. kurz als Gast registrieren.