Ham-Sandwich-Theorem.
Wie kann man
mit einem Schnitt ein Schinken-Sandwich so zerschneiden, daß beide Brothälften und der Schinken jeweils in Teile gleichen Volumens zerlegt werden?

Die Frage hat zwei Aspekte:
1.(theoretisch) gibt es einen solchen Schnitt und
2.(angewandt) wie kann man ihn finden?
Die 1. (theoretische) Frage kann man mit Hilfe des Borsuk-Ulam-Theorems (
Teil 12) beantworten.
Aus dem Borsuk-Ulam-Theorem folgt nämlich das
Ham-Sandwich-Theorem (Banach 1938):
zu drei Teilmengen des Raumes (von endlichem Volumen) gibt es eine Ebene, die alle drei jeweils in Stücke gleichen Volumens teilt.
Dieser Satz gilt übrigens auch, wenn die drei Mengen jeweils aus mehreren Stücken bestehen. Man kann also zum Beispiel mehrere Schichten Schinken, Käse, Brot haben und dann eine Ebene finden, die Schinken, Käse, Brot jeweils gerecht aufteilt (wobei also nicht jede einzelne Käse-Scheibe halbiert wird, sondern nur der Käse insgesamt; entsprechend für den Schinken und das Brot insgesamt.)
 Beweis des Ham-Sandwich-Theorems:
Zunächst bemerken wir, daß es zu jeder Richtung eine senkrecht auf dieser Richtung stehende Ebene gibt, die das Brot genau halbiert, wenn auch nicht unbedingt Käse und Schinken. (Man starte einfach mit einer senkrechten Ebene und verschiebe sie solange bis das Brot genau halbiert wird.)
'Richtungen' entsprechen Punkten auf der Sphäre: wenn man eine Halbgerade vom Nullpunkt in eine bestimmte Richtung zeichnet, schneidet sie die Sphäre in einem bestimmten Punkt.
Dies benutzen wir nun, um eine stetige Funktion f:S2 ---> R2 zu konstruieren: zu einem Punkt x auf der Sphäre (bzw. der zugehörigen 'Richtung') betrachten wir die senkrechte Ebene, die das Brot halbiert und definieren f(x)=(Volumen des Schinkens in der Hälfte von x, Volumen des Käses in der Hälfte von x).
Damit ist dann f(-x)=(Volumen des Schinkens in der Hälfte von -x, Volumen des Käses in der Hälfte von -x). Offenbar liegen x und -x in unterschiedlichen Hälften. Damit ist f(x)=f(-x) genau dann, wenn Schinken und Käse von der Ebene senkrecht zu x halbiert werden.
Nach dem Borsuk-Ulam-Theorem (Teil 12) gibt es ein x auf der Sphäre mit f(x)=f(-x). Die brot-halbierende Ebene senkrecht zu x halbiert also auch Käse und Schinken.
Beweis des Ham-Sandwich-Theorems:
Zunächst bemerken wir, daß es zu jeder Richtung eine senkrecht auf dieser Richtung stehende Ebene gibt, die das Brot genau halbiert, wenn auch nicht unbedingt Käse und Schinken. (Man starte einfach mit einer senkrechten Ebene und verschiebe sie solange bis das Brot genau halbiert wird.)
'Richtungen' entsprechen Punkten auf der Sphäre: wenn man eine Halbgerade vom Nullpunkt in eine bestimmte Richtung zeichnet, schneidet sie die Sphäre in einem bestimmten Punkt.
Dies benutzen wir nun, um eine stetige Funktion f:S2 ---> R2 zu konstruieren: zu einem Punkt x auf der Sphäre (bzw. der zugehörigen 'Richtung') betrachten wir die senkrechte Ebene, die das Brot halbiert und definieren f(x)=(Volumen des Schinkens in der Hälfte von x, Volumen des Käses in der Hälfte von x).
Damit ist dann f(-x)=(Volumen des Schinkens in der Hälfte von -x, Volumen des Käses in der Hälfte von -x). Offenbar liegen x und -x in unterschiedlichen Hälften. Damit ist f(x)=f(-x) genau dann, wenn Schinken und Käse von der Ebene senkrecht zu x halbiert werden.
Nach dem Borsuk-Ulam-Theorem (Teil 12) gibt es ein x auf der Sphäre mit f(x)=f(-x). Die brot-halbierende Ebene senkrecht zu x halbiert also auch Käse und Schinken.
(Neben dieser 3-dimensionalen Version gibt es natürlich mit einem analogen Beweis auch ein 2-dimensionales Ham-Sandwich-Theorem: zu 2 Mengen in der Ebene gibt es eine Gerade, die beide in Stücke gleichen Flächeninhalts zerlegt.)
Die Frage, mehrere Körper gleichzeitig zu halbieren, kommt natürlich in angewandten Problemen vor, z.B. im Zusammenhang mit
'interface reconstruction'. Dabei braucht man dann natürlich nicht nur die Existenz einer halbierenden Ebene, sondern muß sie auch berechnen können.
Zum Beispiel wird das Theorem in
Arbeiten von Blair Swartz angewandt auf 'interface reconstruction in hydrodynamic calculations'.
Applets, mit denen man das einfachere Problem, 2 flache Gebiete in der Ebene durch eine Gerade in Stücke gleichen Flächeninhalts zu zerlegen, durch Probieren lösen kann, findet man
hier bei Chickscope (Egg Math).
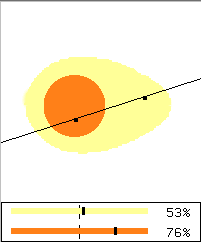
Für Anwendungen in der Informatik benötigt man häufig eine 'diskrete' Version des Ham-Sandwich-Theorems, d.h. man halbiert keine Flächen, sondern Mengen einzelner Punkte. (Zur besseren Unterscheidung denkt man sich die Punkte mit Farben markiert.)
Frage: gegeben sei eine Menge roter und blauer Punkte in der 2-dimensionalen Ebene. Finde eine Gerade, die sowohl die roten als auch die blauen Punkte in zwei gleiche Hälften teilt.
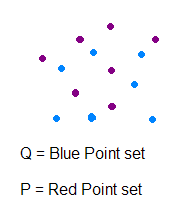
Daß es eine solche Gerade gibt, kann man mit wörtlich demselben Beweis wie für das (2-dimensionale) Ham-Sandwich-Theorem zeigen. Man will aber natürlich nicht nur wissen, daß es die Gerade gibt, sondern sie auch finden. Aus dem Existenzbeweis kann man im Prinzip einen Algorithmus bekommen, der allerdings nicht sehr effektiv ist.
Die Frage, ob es einen Algorithmus gibt, der effektiv ist (d.h. dessen Laufzeit eine lineare Funktion der Anzahl der Punkte ist), war lange offen.
Ein Algorithmus, dessen Laufzeit linear von der Anzahl der Punkte abhängt, wurde erst 1990 von Lo and Steiger gefunden.
Eine Beschreibung dieses Algorithmus findet man
bei D.MacNevin.
Für das 3-dimensionale diskrete Problem wurde ein Algorithmus in linearer Zeit 1994 von Lo, Matousek und Steiger gefunden.
Teil 1,
Teil 2,
Teil 3,
Teil 4,
Teil 5,
Teil 6,
Teil 7 ,
Teil 8,
Teil 9 ,
Teil 10 ,
Teil 11,
Teil 12  Beweis des Ham-Sandwich-Theorems:
Zunächst bemerken wir, daß es zu jeder Richtung eine senkrecht auf dieser Richtung stehende Ebene gibt, die das Brot genau halbiert, wenn auch nicht unbedingt Käse und Schinken. (Man starte einfach mit einer senkrechten Ebene und verschiebe sie solange bis das Brot genau halbiert wird.)
'Richtungen' entsprechen Punkten auf der Sphäre: wenn man eine Halbgerade vom Nullpunkt in eine bestimmte Richtung zeichnet, schneidet sie die Sphäre in einem bestimmten Punkt.
Dies benutzen wir nun, um eine stetige Funktion f:S2 ---> R2 zu konstruieren: zu einem Punkt x auf der Sphäre (bzw. der zugehörigen 'Richtung') betrachten wir die senkrechte Ebene, die das Brot halbiert und definieren f(x)=(Volumen des Schinkens in der Hälfte von x, Volumen des Käses in der Hälfte von x).
Damit ist dann f(-x)=(Volumen des Schinkens in der Hälfte von -x, Volumen des Käses in der Hälfte von -x). Offenbar liegen x und -x in unterschiedlichen Hälften. Damit ist f(x)=f(-x) genau dann, wenn Schinken und Käse von der Ebene senkrecht zu x halbiert werden.
Nach dem Borsuk-Ulam-Theorem (Teil 12) gibt es ein x auf der Sphäre mit f(x)=f(-x). Die brot-halbierende Ebene senkrecht zu x halbiert also auch Käse und Schinken.
(Neben dieser 3-dimensionalen Version gibt es natürlich mit einem analogen Beweis auch ein 2-dimensionales Ham-Sandwich-Theorem: zu 2 Mengen in der Ebene gibt es eine Gerade, die beide in Stücke gleichen Flächeninhalts zerlegt.)
Die Frage, mehrere Körper gleichzeitig zu halbieren, kommt natürlich in angewandten Problemen vor, z.B. im Zusammenhang mit 'interface reconstruction'. Dabei braucht man dann natürlich nicht nur die Existenz einer halbierenden Ebene, sondern muß sie auch berechnen können.
Zum Beispiel wird das Theorem in Arbeiten von Blair Swartz angewandt auf 'interface reconstruction in hydrodynamic calculations'.
Applets, mit denen man das einfachere Problem, 2 flache Gebiete in der Ebene durch eine Gerade in Stücke gleichen Flächeninhalts zu zerlegen, durch Probieren lösen kann, findet man hier bei Chickscope (Egg Math).
Beweis des Ham-Sandwich-Theorems:
Zunächst bemerken wir, daß es zu jeder Richtung eine senkrecht auf dieser Richtung stehende Ebene gibt, die das Brot genau halbiert, wenn auch nicht unbedingt Käse und Schinken. (Man starte einfach mit einer senkrechten Ebene und verschiebe sie solange bis das Brot genau halbiert wird.)
'Richtungen' entsprechen Punkten auf der Sphäre: wenn man eine Halbgerade vom Nullpunkt in eine bestimmte Richtung zeichnet, schneidet sie die Sphäre in einem bestimmten Punkt.
Dies benutzen wir nun, um eine stetige Funktion f:S2 ---> R2 zu konstruieren: zu einem Punkt x auf der Sphäre (bzw. der zugehörigen 'Richtung') betrachten wir die senkrechte Ebene, die das Brot halbiert und definieren f(x)=(Volumen des Schinkens in der Hälfte von x, Volumen des Käses in der Hälfte von x).
Damit ist dann f(-x)=(Volumen des Schinkens in der Hälfte von -x, Volumen des Käses in der Hälfte von -x). Offenbar liegen x und -x in unterschiedlichen Hälften. Damit ist f(x)=f(-x) genau dann, wenn Schinken und Käse von der Ebene senkrecht zu x halbiert werden.
Nach dem Borsuk-Ulam-Theorem (Teil 12) gibt es ein x auf der Sphäre mit f(x)=f(-x). Die brot-halbierende Ebene senkrecht zu x halbiert also auch Käse und Schinken.
(Neben dieser 3-dimensionalen Version gibt es natürlich mit einem analogen Beweis auch ein 2-dimensionales Ham-Sandwich-Theorem: zu 2 Mengen in der Ebene gibt es eine Gerade, die beide in Stücke gleichen Flächeninhalts zerlegt.)
Die Frage, mehrere Körper gleichzeitig zu halbieren, kommt natürlich in angewandten Problemen vor, z.B. im Zusammenhang mit 'interface reconstruction'. Dabei braucht man dann natürlich nicht nur die Existenz einer halbierenden Ebene, sondern muß sie auch berechnen können.
Zum Beispiel wird das Theorem in Arbeiten von Blair Swartz angewandt auf 'interface reconstruction in hydrodynamic calculations'.
Applets, mit denen man das einfachere Problem, 2 flache Gebiete in der Ebene durch eine Gerade in Stücke gleichen Flächeninhalts zu zerlegen, durch Probieren lösen kann, findet man hier bei Chickscope (Egg Math).
 Für Anwendungen in der Informatik benötigt man häufig eine 'diskrete' Version des Ham-Sandwich-Theorems, d.h. man halbiert keine Flächen, sondern Mengen einzelner Punkte. (Zur besseren Unterscheidung denkt man sich die Punkte mit Farben markiert.)
Frage: gegeben sei eine Menge roter und blauer Punkte in der 2-dimensionalen Ebene. Finde eine Gerade, die sowohl die roten als auch die blauen Punkte in zwei gleiche Hälften teilt.
Für Anwendungen in der Informatik benötigt man häufig eine 'diskrete' Version des Ham-Sandwich-Theorems, d.h. man halbiert keine Flächen, sondern Mengen einzelner Punkte. (Zur besseren Unterscheidung denkt man sich die Punkte mit Farben markiert.)
Frage: gegeben sei eine Menge roter und blauer Punkte in der 2-dimensionalen Ebene. Finde eine Gerade, die sowohl die roten als auch die blauen Punkte in zwei gleiche Hälften teilt.
 Daß es eine solche Gerade gibt, kann man mit wörtlich demselben Beweis wie für das (2-dimensionale) Ham-Sandwich-Theorem zeigen. Man will aber natürlich nicht nur wissen, daß es die Gerade gibt, sondern sie auch finden. Aus dem Existenzbeweis kann man im Prinzip einen Algorithmus bekommen, der allerdings nicht sehr effektiv ist.
Die Frage, ob es einen Algorithmus gibt, der effektiv ist (d.h. dessen Laufzeit eine lineare Funktion der Anzahl der Punkte ist), war lange offen.
Ein Algorithmus, dessen Laufzeit linear von der Anzahl der Punkte abhängt, wurde erst 1990 von Lo and Steiger gefunden.
Eine Beschreibung dieses Algorithmus findet man bei D.MacNevin.
Für das 3-dimensionale diskrete Problem wurde ein Algorithmus in linearer Zeit 1994 von Lo, Matousek und Steiger gefunden.
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12
Daß es eine solche Gerade gibt, kann man mit wörtlich demselben Beweis wie für das (2-dimensionale) Ham-Sandwich-Theorem zeigen. Man will aber natürlich nicht nur wissen, daß es die Gerade gibt, sondern sie auch finden. Aus dem Existenzbeweis kann man im Prinzip einen Algorithmus bekommen, der allerdings nicht sehr effektiv ist.
Die Frage, ob es einen Algorithmus gibt, der effektiv ist (d.h. dessen Laufzeit eine lineare Funktion der Anzahl der Punkte ist), war lange offen.
Ein Algorithmus, dessen Laufzeit linear von der Anzahl der Punkte abhängt, wurde erst 1990 von Lo and Steiger gefunden.
Eine Beschreibung dieses Algorithmus findet man bei D.MacNevin.
Für das 3-dimensionale diskrete Problem wurde ein Algorithmus in linearer Zeit 1994 von Lo, Matousek und Steiger gefunden.
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12 


