Raumfüllende Kurven in Mathematik, Philosophie und Musik.
Am Mittwoch war der 150. Geburtstag von
Giuseppe Peano, jedem Mathe-Erstsemester bekannt durch die
Peano-Axiome (die einfach noch einmal streng formal die aus der Schule bekannten Eigenschaften der natürlichen Zahlen und das Prinzip der vollständigen Induktion zusammenfassen).
Außerdem, und das paßt jetzt in diese Reihe zur Poincare-Vermutung und Fundamentalgruppe, geht auf ihn die Konstruktion von
raumfüllenden Kurven (heute als Peano-Kurven bekannt) zurück.
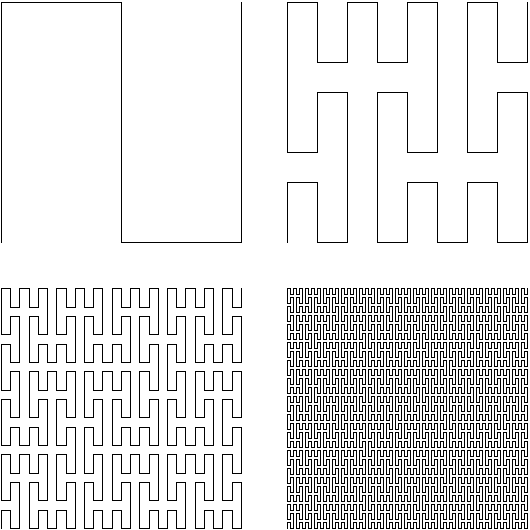
Das Bild zeigt vier Stufen einer Konstruktion von Kurven, die das Einheitsquadrat immer dichter ausfüllen. Es ist klar, daß man auf analoge Weise immer dichtere Kurven bilden kann. Im Grenzwert bekommt man eine Kurve, die das gesamte Quadrat ausfüllt, die
Peano-Kurve, deren Bild also so aussieht:

Okay, das war jetzt nicht so originell. (Das Bild ist übrigens
ein Kunstwerk von Kasimir Malevich aus dem Jahr 1913. Im Ernst.)
Der Zusammenhang mit dem Thema dieser Reihe ist, daß
Peano-Kurven scheinbar (aber nicht tatsächlich) die Aussage widerlegen könnten, daß die
Sphäre einfach zusammenhängend ist (d.h. daß sich jede Kurve in einen Punkt deformieren läßt). Auch wenn dies der Aspekt von Peano-Kurven ist, der mich eigentlich interessiert, verschiebe ich das aus Platzgründen auf nächste Woche.
Peano war allgemein dafür bekannt,
Gegenbeispiele zu bekannten Vermutungen zu konstruieren, dadurch einerseits manche Irrtümer aufzudecken und andererseits die Notwendigkeit klar definierter Annahmen zu zeigen. (Z.B. für
Existenz & Eindeutigkeit der Lösungen gewöhnlicher Differentialgleichungen.) Er gilt auch als Begründer der
symbolischen Logik. Die heute üblichen Symbole für Durchschnitte, Vereinigungen, Elementbeziehung oder Existenzquantor gehen auf Peano zurück.
Die scheinbar abwegige Tatsache, daß eine
(eindimensionale) Kurve genau so viele Punkte haben kann
wie das (zweidimensionale) Quadrat, interessiert immer wieder auch Leute außerhalb der Mathematik:
Peano-Kurven kommen gelegentlich in philosophischen Diskussionen vor (z.B. Seite 12
dieses Vortrags von B. Kanitscheider).
Auf YouTube findet man sogar Goethe's Erlkönig auf einer Peano-Kurve wandernd (
"Gosper Peano Curve" von Neptune1300):
Wer statt klassichem Gesang lieber elektronische Musik mag, dem wird diese Version vielleicht besser gefallen (
Peano-Gosper Curve von Alanonala):
Die Peano-Kurven sind aber nicht nur eine Kuriosität bzw. ein potentielles Gegenbeispiel zu zu einfachen Vermutungen, sondern spielen heute eine wichtige Rolle als technisches Hilfsmittel in einem zentralen Teilgebiet der 3-dimensionalen Topologie, der
Cannon-Thurston-Theorie.
Auch auf einem ganz anderen Gebiet hat sich Peano einen Namen gemacht, nämlich durch die Entwicklung der Plansprache
Latino sin flexione. Diese Sprache hatte denselben Wortschatz wie Latein, aber nicht die komplizierte Grammatik. Er wollte damit Latein als Weltsprache wiederbeleben. Aus der Wikipedia:"
Peano begründete seine Sprache in dem Artikel De Latino sine Flexione, Lingua Auxiliare Internationale (= Über das Latein ohne Beugung, eine internationale Hilfssprache). Darin argumentiert er, Welthilfssprachen seien unnötig, da es schon Latein als Weltsprache gebe. Peano begann seinen Artikel über Latino sine flexione in normalem Latein, ließ dann nach und nach alle Flexionen weg, bis das Ende des Artikels vollständig in Latino sine flexione zu lesen war." Im Gegensatz zu anderen Plansprachen fand Latino sin flexione durchaus Anwendung, zumindest als Sprache für einige wissenschaftlichen Publikationen.
Teil 1, Teil 2, Teil 3, Teil 4, Teil 5, Teil 6, Teil 7 , Teil 8, Teil 9 , Teil 10 ,Teil 11, Teil 12, Teil 13, Teil 14, Teil 15, Teil 16, Teil 17, Teil 18, Teil 19, Teil 20, Teil 21, Teil 22, Teil 23, Teil 24, Teil 25, Teil 26, Teil 27, Teil 28
 Das Bild zeigt vier Stufen einer Konstruktion von Kurven, die das Einheitsquadrat immer dichter ausfüllen. Es ist klar, daß man auf analoge Weise immer dichtere Kurven bilden kann. Im Grenzwert bekommt man eine Kurve, die das gesamte Quadrat ausfüllt, die Peano-Kurve, deren Bild also so aussieht:
Das Bild zeigt vier Stufen einer Konstruktion von Kurven, die das Einheitsquadrat immer dichter ausfüllen. Es ist klar, daß man auf analoge Weise immer dichtere Kurven bilden kann. Im Grenzwert bekommt man eine Kurve, die das gesamte Quadrat ausfüllt, die Peano-Kurve, deren Bild also so aussieht:
 Okay, das war jetzt nicht so originell. (Das Bild ist übrigens ein Kunstwerk von Kasimir Malevich aus dem Jahr 1913. Im Ernst.)
Der Zusammenhang mit dem Thema dieser Reihe ist, daß Peano-Kurven scheinbar (aber nicht tatsächlich) die Aussage widerlegen könnten, daß die Sphäre einfach zusammenhängend ist (d.h. daß sich jede Kurve in einen Punkt deformieren läßt). Auch wenn dies der Aspekt von Peano-Kurven ist, der mich eigentlich interessiert, verschiebe ich das aus Platzgründen auf nächste Woche.
Peano war allgemein dafür bekannt, Gegenbeispiele zu bekannten Vermutungen zu konstruieren, dadurch einerseits manche Irrtümer aufzudecken und andererseits die Notwendigkeit klar definierter Annahmen zu zeigen. (Z.B. für Existenz & Eindeutigkeit der Lösungen gewöhnlicher Differentialgleichungen.) Er gilt auch als Begründer der symbolischen Logik. Die heute üblichen Symbole für Durchschnitte, Vereinigungen, Elementbeziehung oder Existenzquantor gehen auf Peano zurück.
Die scheinbar abwegige Tatsache, daß eine (eindimensionale) Kurve genau so viele Punkte haben kann wie das (zweidimensionale) Quadrat, interessiert immer wieder auch Leute außerhalb der Mathematik:
Peano-Kurven kommen gelegentlich in philosophischen Diskussionen vor (z.B. Seite 12 dieses Vortrags von B. Kanitscheider).
Auf YouTube findet man sogar Goethe's Erlkönig auf einer Peano-Kurve wandernd ("Gosper Peano Curve" von Neptune1300):
Okay, das war jetzt nicht so originell. (Das Bild ist übrigens ein Kunstwerk von Kasimir Malevich aus dem Jahr 1913. Im Ernst.)
Der Zusammenhang mit dem Thema dieser Reihe ist, daß Peano-Kurven scheinbar (aber nicht tatsächlich) die Aussage widerlegen könnten, daß die Sphäre einfach zusammenhängend ist (d.h. daß sich jede Kurve in einen Punkt deformieren läßt). Auch wenn dies der Aspekt von Peano-Kurven ist, der mich eigentlich interessiert, verschiebe ich das aus Platzgründen auf nächste Woche.
Peano war allgemein dafür bekannt, Gegenbeispiele zu bekannten Vermutungen zu konstruieren, dadurch einerseits manche Irrtümer aufzudecken und andererseits die Notwendigkeit klar definierter Annahmen zu zeigen. (Z.B. für Existenz & Eindeutigkeit der Lösungen gewöhnlicher Differentialgleichungen.) Er gilt auch als Begründer der symbolischen Logik. Die heute üblichen Symbole für Durchschnitte, Vereinigungen, Elementbeziehung oder Existenzquantor gehen auf Peano zurück.
Die scheinbar abwegige Tatsache, daß eine (eindimensionale) Kurve genau so viele Punkte haben kann wie das (zweidimensionale) Quadrat, interessiert immer wieder auch Leute außerhalb der Mathematik:
Peano-Kurven kommen gelegentlich in philosophischen Diskussionen vor (z.B. Seite 12 dieses Vortrags von B. Kanitscheider).
Auf YouTube findet man sogar Goethe's Erlkönig auf einer Peano-Kurve wandernd ("Gosper Peano Curve" von Neptune1300):



