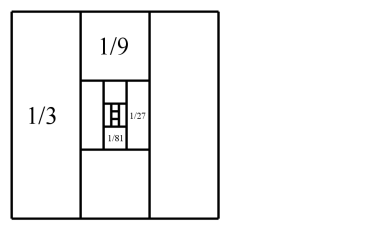
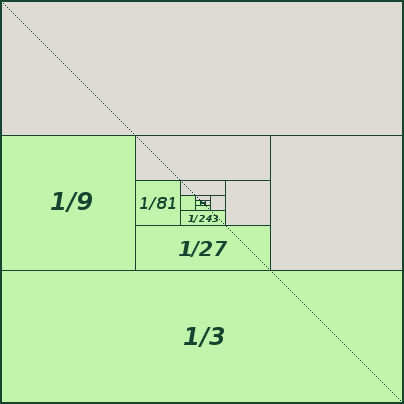
1/3 + 1/9 + 1/27 + ... = 1/2 mit Dreiecken statt Rechtecken. Wir hatten hier mal über einige Veranschaulichungen unendlicher Summen geschrieben, zum Beispiel über das Bild oben (von Big Ideas), das die Summe 1/3 + 1/9 + 1/27 + ... = 1/2 visualisiert. Eine im Prinzip äquivalente Veranschaulichung derselben Summe findet man bei Bill the Lizard: Man muß hier natürlich kurz nachdenken, warum die Summe gerade 1/2 ist, also warum die grünen Flächen über der Diagonale gerade den grauen Flächen unter der Diagonale entsprechen. In einem anderen Beitrag hatten wir mal (am Beispiel der Summe 1/4 + 1/16 + 1/64 + 1/256 + ...) diskutiert, ob Veranschaulichungen mit Dreiecken "besser" sind als Veranschaulichungen mit Quadraten. (Auch in der Topologie definiert man singuläre Homologie ja lieber mit Simplizes statt mit Würfeln.) Bei Matt Henderson findet sich jetzt (neben vielen anderen interessanten Visualisierungen) auch noch eine Veranschaulichung von 1/3 + 1/9 + 1/27 + ... = 1/2 mit Dreiecken statt Quadraten. 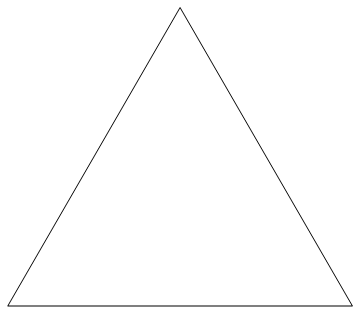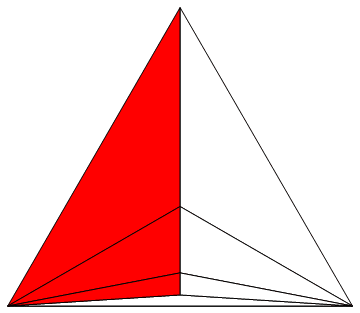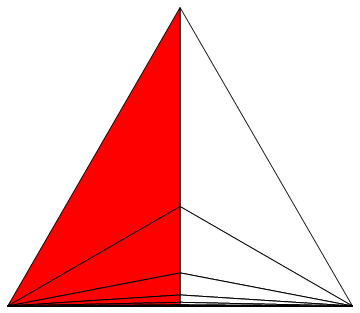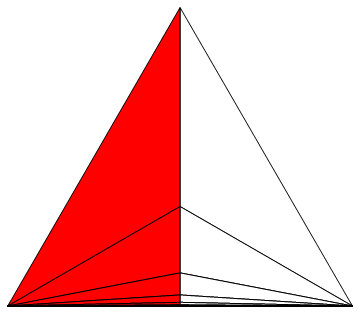Man erkennt jedenfalls sofort, daß die Summe 1/2 ist. Dafür muß man diesmal vielleicht kurz überlegen, warum die Summanden 1/3ⁿ sind. Visualisierung unendlicher Summen I Visualisierung unendlicher Summen II

Um einen Kommentar zu verfassen, müssen Sie sich einloggen bzw. kurz als Gast registrieren.