1+2+...+(n-1) ist "n über 2", d.h. die Anzahl der Möglichkeiten 2 Elemente aus einer n-elementigen Menge auszuwählen:
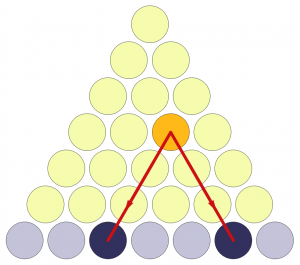Es gibt n blaue und 1+2+...+(n-1) gelbe Kugeln. Jedes Paar von blauen Kugeln entspricht einer eindeutigen gelben.
12+22+...+n2=n(n+1)(n+1/2)/3:
Dieses Beispiel von Man Keung Siu ist vielleicht nicht so offensichtlich. Die drei Pyramiden bestehen jeweils aus 12+22+...+n2 Würfeln und sie passen genau zusammen zu einem Quader mit Kantenlängen n, n+1 und n+1/2.
Für die durch F0=1,F1=1, Fn=Fn-1+Fn-2 definierten Fibonacci-Zahlen gilt die Gleichung F02+F12+...+Fn2=FnFn+1:
Das grosse Rechteck hat Flächeninhalt FnFn+1, die kleinen Quadrate haben jeweils Flächeninhalt Fi2 und der Grund, dass die kleinen Quadrate sich zu einem Rechtck zusammenfügen ist natürlich die Voraussetzung Fn=Fn-1+Fn-2.
x3/3+y3/3+z3/3 ≥ xyz:
Auch in diesem Bild von Darsh Ranjan muss man sich natürlich erstmal klarmachen, dass alles zusammenpasst. Der Jeder Topologe kennt den Beweis, dass Homotopiegruppen πn(X,x) (eines beliebigen Raumes X mit Basispunkt x) für n≥2 abelsch sind:
f und g sind Abbildungen von Dn nach X, die auf dem Rand konstant x sind. Die Hintereinanderausführungen fg bzw. gf werden durch die Bilder links und rechts definiert. Dazwischen hat man die Homotopie, wobei Punkte ausserhalb der inneren Rechtecke alle auf x abgebildet werden.
Und dann ist da noch der Beweis (aus Kock: Frobenius Algebras and 2-D Topological Quantum Field Theories), dass in einer Frobeniusalgebra die Komultiplikation genau dann kokommutativ ist, wenn die Multiplikation kommutativ ist:
