The starting point of “IUTeich” (i.e., Inter-universal Teichmüller Theory) lies in the image of a sequence of nested universes. This sort of image apparently goes back to ancient times and appears not only in the “Sokkuri Hausu” (i.e., “Identical House”) animation discussed here, but in various stories and myths all over the world. In the case of IUTeich, the various universes correspond to “classical arithmetic geometry theaters in which conventional ring theory/scheme theory is valid”. In the “Sokkuri animation”, these universes are represented by “houses”. Within each classical arithmetic geometry theater, one has a theta function; it is this theta function that plays the role of “Frobenioid-theoretic” (i.e., non-scheme-theoretic! — cf. Frobenioids I, II; ´Etale Theta) “bridge” to the “next universe”. In the “Sokkuri animation”, this link furnished by the theta function corresponds to the gaze of the little girl into the “small house”. Indeed, the large eyes of the little girl look somewhat like thetas Θ! In IUTeich, Galois groups and arithmetic fundamental groups behave as though they are made of a “mysterious substance” that allows them to pass freely, in an isomorphic fashion, between the various universes without being subject to expansion or contraction. In the “Sokkuri animation”, this “mysterious substance” corresponds to the “mysterious stars” that form the link between the “small” and “large” houses. The rotation of these “mysterious stars” may be thought of, relative to IUTeich, as representing the nature of the “´etalelike structures” that occur in the theory of Frobenioids (cf. Frobenioids I, II) or, alternatively, as corresponding to the rotation of addition and multiplication that occurs in the mono-anabelian theory of Topics III. The deepest and most pivotal portion of IUTeich consists of a certain canonical splitting of the sequence of nested universes, a splitting which is constructed by means of the mono-anabelian theory of Topics III and the various rigidity properties of the ´etale theta function (cf. ´Etale Theta for more on the latter). This canonical splitting corresponds to the canonical liftings of pTeich (i.e., p-adic Teichmüller theory) or, at a more elementary level, the Teichmüller representatives of a Witt ring. (Incidentally, in the p-adic theory, the various “universes” of IUTeich correspond to the various positive characteristic algebraic geometries contained in the various subquotients “pn/pn+1”.)(Die "Sokkuri Animation" ist hier.) Aber nach allem, was sich im Netz dazu findet, scheint es sich um einen ziemlich revolutionären neuen Zugang zur arithmetischen Geometrie, der Theorie der Schemata über Spec(Z), zu handeln, siehe zum Beispiel den Beitrag von Minhyong Kim auf Math Overflow. Weil es sich um eine völlig neu entwickelte Theorie handelt, wird die Überprüfung sicher noch eine Weile dauern.
abc-Vermutung bewiesen?
Die abc-Vermutung ist so etwas wie der gegenwärtige heilige Gral der Zahlentheorie, so wie früher mal die Fermat-Vermutung oder die Taniyama-Shimura-Vermutung
Es geht ganz banal um Lösungen der Gleichung
a+b=c
in ganzen Zahlen a,b,c, die man (nach Herauskürzen eines gemeinsamen Teilers) als teilerfremd annehmen kann. Die Behauptung der abc-Vermutung ist dann für teilerfremde a,b,c:
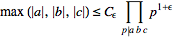 wobei Cε von ε abhängt. (Soll heissen: für jedes ε>0 gibt es ein Cε, so dass für alle teilerfremden Lösungen von a+b=c die obige Ungleichung gilt.)
Aus der abc-Vermutung folgt die Fermat-Vermutung zumindest für grosse Exponenten: wenn man eine (positive ganzzahlige) Lösung der Fermat-Gleichung An+Bn=Cn hat, setzt man a=An, b=Bn,c=Cn und kann dann leicht nachrechnen, dass c grösser als das Produkt aller pn/3 über die Primteiler von abc ist. Für grosse n ist das natürlich ein Widerspruch zu obiger Ungleichung.
Diese und andere Folgerungen (u.a. einen Beweis der ursprünglich von Faltings bewiesenen Mordell-Vermutung) sowie die Verbindungen zu elliptischen Kurven und Modulformen findet man in diesem Übersichtsartikel von Mazur. (Wikipedia listet noch eine Reihe weiterer offener Vermutungen, die aus abc folgen würden.)
Die abc-Vermutung ist jetzt vielleicht von Shinichi Mochizuki bewiesen worden. Gerüchte darüber hatte es schon seit 3 Monaten gegeben, seit Dienstag ist nun der Preprint INTER-UNIVERSAL TEICHMÜLLER THEORY IV: LOG-VOLUME COMPUTATIONS AND SET-THEORETIC FOUNDATIONS online.
Das Paper wirkt (vom rein äusserlichen Eindruck her) zunächst ziemlich ungewöhnlich, beginnend mit dem Titel, ein Eindruck, der sich noch verstärkt, wenn man die Erläuterungen auf der Webseite des Autors anschaut:
wobei Cε von ε abhängt. (Soll heissen: für jedes ε>0 gibt es ein Cε, so dass für alle teilerfremden Lösungen von a+b=c die obige Ungleichung gilt.)
Aus der abc-Vermutung folgt die Fermat-Vermutung zumindest für grosse Exponenten: wenn man eine (positive ganzzahlige) Lösung der Fermat-Gleichung An+Bn=Cn hat, setzt man a=An, b=Bn,c=Cn und kann dann leicht nachrechnen, dass c grösser als das Produkt aller pn/3 über die Primteiler von abc ist. Für grosse n ist das natürlich ein Widerspruch zu obiger Ungleichung.
Diese und andere Folgerungen (u.a. einen Beweis der ursprünglich von Faltings bewiesenen Mordell-Vermutung) sowie die Verbindungen zu elliptischen Kurven und Modulformen findet man in diesem Übersichtsartikel von Mazur. (Wikipedia listet noch eine Reihe weiterer offener Vermutungen, die aus abc folgen würden.)
Die abc-Vermutung ist jetzt vielleicht von Shinichi Mochizuki bewiesen worden. Gerüchte darüber hatte es schon seit 3 Monaten gegeben, seit Dienstag ist nun der Preprint INTER-UNIVERSAL TEICHMÜLLER THEORY IV: LOG-VOLUME COMPUTATIONS AND SET-THEORETIC FOUNDATIONS online.
Das Paper wirkt (vom rein äusserlichen Eindruck her) zunächst ziemlich ungewöhnlich, beginnend mit dem Titel, ein Eindruck, der sich noch verstärkt, wenn man die Erläuterungen auf der Webseite des Autors anschaut:



