Besonders minimalistisch geht es im Dezemberblatt des KIAS-Wandkalenders zu: die einfachsten Knoten, die einfachste projektive Ebene, die einfachste topologische Formel. Und noch allerlei Überraschendes aus Elementargeometrie, elementarer Zahlentheorie und dem Rechnen mit divergenten Reihen.
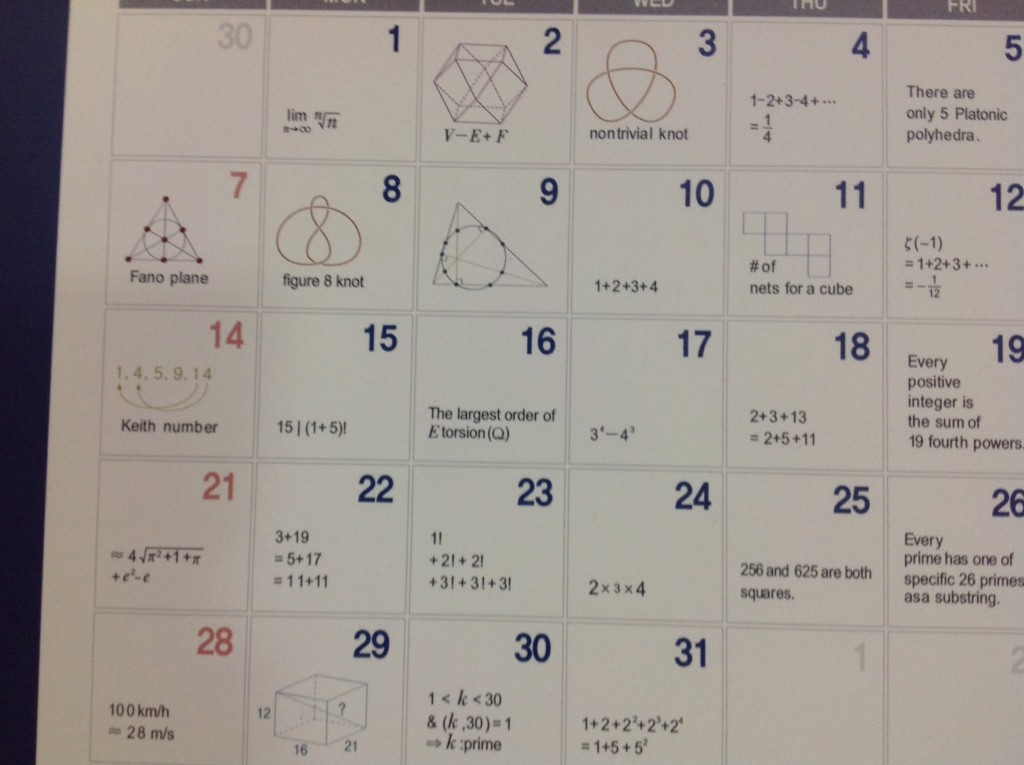
Im Dezember ist alles besonders einfach: die
2 zeigt den einfachsten und ältesten topologischen Lehrsatz: die Berechnung der
Euler-Charakteristik der 2-dimensionalen Sphäre; die
3 zeigt den (nach dem
Unknoten) einfachsten Knoten: die
Kleeblattschlinge, und die
8 den einfachsten
hyperbolischen Knoten: den
Achterknoten; die
7 schließlich zeigt die einfachste projektive Ebene: die
Fano-Ebene.
Die
9 zeigt die neun besonderen Punkte auf dem
Feuerbachkreis und die
11 eine der elf Möglichkeiten, ein Würfelnetz in der Ebene auszulegen.
Bei der
12 (Bild unten) geht es darum, weshalb die paradoxe Gleichung
\(1+2+3+4+5+\ldots = -\frac{1}{12} \)
Sinn macht - darüber hatten wir im Januar mal
was geschrieben. (Übrigens der
meistgelesene Mathlog-Artikel bisher in diesem Jahr.) Ein anderes Beispiel einer divergenten Reihe steht bei der
4:
1 − 2 + 3 − 4 + ⋯
Keith-Zahlen werden auch als "repfigit numbers" (für "
repetitive
Fibonacci-like di
git") bezeichnet,
14 ist die kleinste von ihnen.
Auf elliptischen Kurven kann man eine "Addition" definieren, was in der Kryptographie äußerst nützlich ist. (Siehe
Kryptographie X.) Manche rationalen Punkte haben dann endliche Ordnung, d.h. durch wiederholtes Addieren desselben Punktes bekommt man am Ende wieder das neutrale Element (den Punkt im Unendlichen). Solche Punkte endlicher Ordnung bezeichnet man als Torsionspunkte und erstaunlicherweise kann die Ordnung eines rationalen Punktes nie größer als
16 sein. (Nachtrag, siehe Kommentare: die Ordnung eines rationalen Punktes kann sogar nie größer als 12 sein. Die maximale Ordnung der Gruppe aller Torsionselemente ist 16.)
Dass man jede Zahl als Summe von
19 vierten Potenzen \(n=x_1^4+x_2^4+\ldots+x_{19}^4 \) zerlegen kann, ist ein Spezialfall des
Waringschen Problems, bewiesen wurde es erst 1986 von
Ramachandran Balasubramanian.
Ziemlich überraschend finde ich, dass jede Primzahl - wenn man sie im Dezimalsystem aufschreibt -- eine der folgenden
26 minimalen Primzahlen als "Teilstring" enthält: 2, 3, 5, 7, 11, 19, 41, 61, 89, 409, 449, 499, 881, 991, 6469, 6949, 9001, 9049, 9649, 9949, 60649, 666649, 946669, 60000049, 66000049, 66600049. Das wurde wohl
erst 2001 von Jeffrey Shallit herausgefunden.
Die bisherigen Blätter:
November
Oktober
September
August
Juli und an dessen Ende die Links zu März-Juni.
Im Dezember ist alles besonders einfach: die 2 zeigt den einfachsten und ältesten topologischen Lehrsatz: die Berechnung der Euler-Charakteristik der 2-dimensionalen Sphäre; die 3 zeigt den (nach dem Unknoten) einfachsten Knoten: die Kleeblattschlinge, und die 8 den einfachsten hyperbolischen Knoten: den Achterknoten; die 7 schließlich zeigt die einfachste projektive Ebene: die Fano-Ebene.
Die 9 zeigt die neun besonderen Punkte auf dem Feuerbachkreis und die 11 eine der elf Möglichkeiten, ein Würfelnetz in der Ebene auszulegen.
Bei der 12 (Bild unten) geht es darum, weshalb die paradoxe Gleichung
\(1+2+3+4+5+\ldots = -\frac{1}{12} \)
Sinn macht - darüber hatten wir im Januar mal was geschrieben. (Übrigens der meistgelesene Mathlog-Artikel bisher in diesem Jahr.) Ein anderes Beispiel einer divergenten Reihe steht bei der 4: 1 − 2 + 3 − 4 + ⋯
Keith-Zahlen werden auch als "repfigit numbers" (für "repetitive Fibonacci-like digit") bezeichnet, 14 ist die kleinste von ihnen.
Auf elliptischen Kurven kann man eine "Addition" definieren, was in der Kryptographie äußerst nützlich ist. (Siehe Kryptographie X.) Manche rationalen Punkte haben dann endliche Ordnung, d.h. durch wiederholtes Addieren desselben Punktes bekommt man am Ende wieder das neutrale Element (den Punkt im Unendlichen). Solche Punkte endlicher Ordnung bezeichnet man als Torsionspunkte und erstaunlicherweise kann die Ordnung eines rationalen Punktes nie größer als 16 sein. (Nachtrag, siehe Kommentare: die Ordnung eines rationalen Punktes kann sogar nie größer als 12 sein. Die maximale Ordnung der Gruppe aller Torsionselemente ist 16.)
Dass man jede Zahl als Summe von 19 vierten Potenzen \(n=x_1^4+x_2^4+\ldots+x_{19}^4 \) zerlegen kann, ist ein Spezialfall des Waringschen Problems, bewiesen wurde es erst 1986 von Ramachandran Balasubramanian.
Ziemlich überraschend finde ich, dass jede Primzahl - wenn man sie im Dezimalsystem aufschreibt -- eine der folgenden 26 minimalen Primzahlen als "Teilstring" enthält: 2, 3, 5, 7, 11, 19, 41, 61, 89, 409, 449, 499, 881, 991, 6469, 6949, 9001, 9049, 9649, 9949, 60649, 666649, 946669, 60000049, 66000049, 66600049. Das wurde wohl erst 2001 von Jeffrey Shallit herausgefunden.
Die bisherigen Blätter:
November
Oktober
September
August
Juli und an dessen Ende die Links zu März-Juni.