Ramsey-Zahlen, Euler-Charakteristiken und das Stomachion.
Der Eintrag bei der
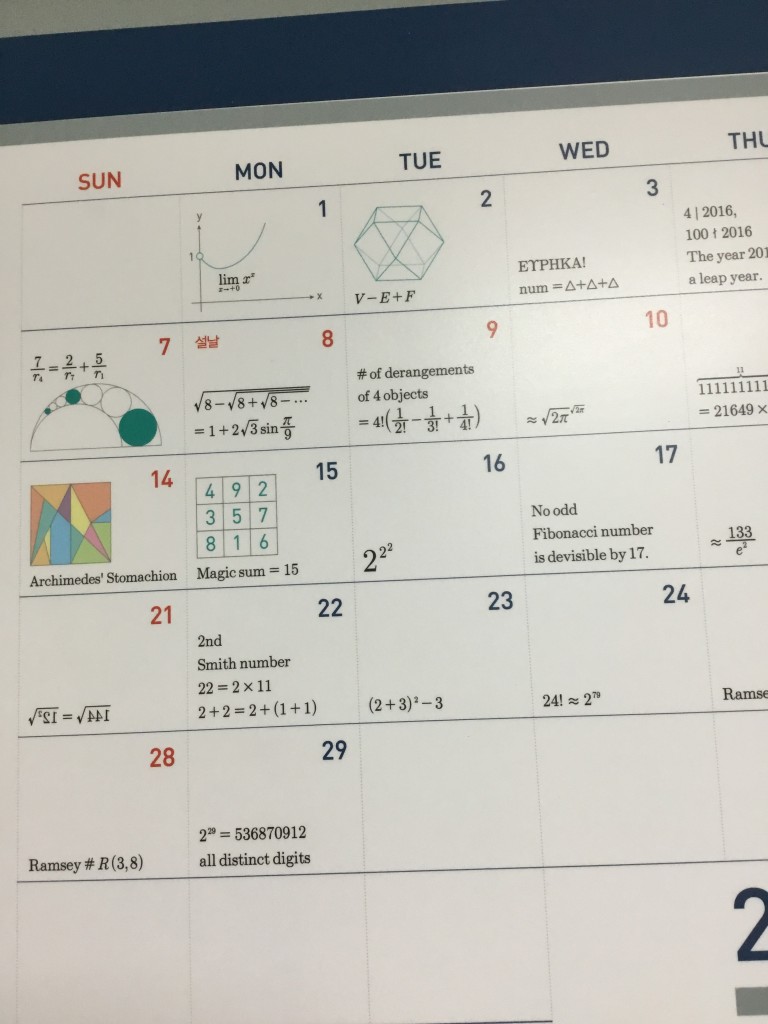
1 zeigt den Graphen von \(f(x)=x^x\), der sein Minimum in 1/e hat und für x->0 gegen 1 strebt, was man zum Beispiel mittels der Substitution x=1/n aus \(\lim_{n\to\infty}\sqrt[n]{n}=1\) oder auch aus \(\lim_{n\to\infty}\frac{\ln(n)}{n}=0\) herleiten kann.
Der Eintrag bei der
2 zeigt die Eulersche Polyederformel: für einen konvexen Polyeder mit V Ecken, E Kanten und F Flächen hat man V-E+F=2. Mit heutiger Mathematik läßt sich das so begründen, dass konvexe Polyeder homöomorph zur Sphäre sind und die Euler-Charakteristik der Sphäre 2 ist. Siehe
TvF 4.
Der Eintrag bei der
3 bezieht sich auf das 1796 von Gauss bewiesene Eureka-Theorem, demzufolge sich jede natürliche Zahl als Summe dreier
Dreieckszahlen zerlegen läßt, eine der vielen unbewiesenen Vermutungen von Pierre de Fermat.
Der vollständige Graph auf
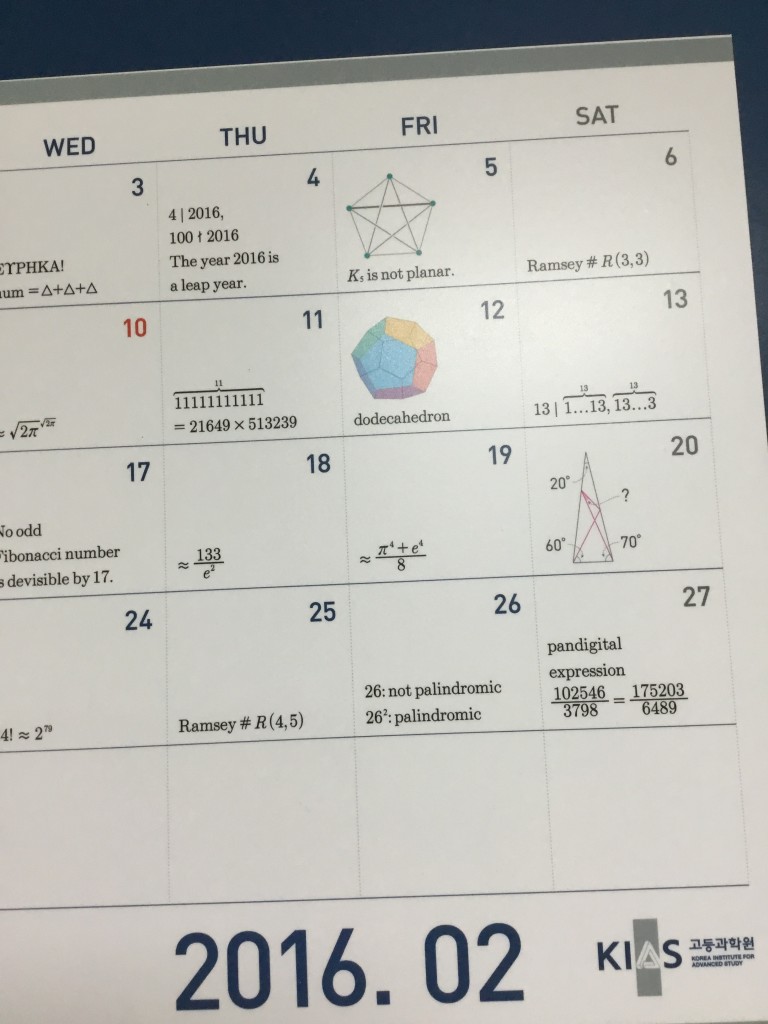
5 Ecken (Bild unten) läßt sich nicht kreuzungsfrei in die Ebene einbetten, beweisen kann man das zum Beispiel mit der Euler-Charakteristik.
Den Sinus von pi/9 kann man im Prinzip mittels der trigonometrischen Identität sin(3x)=3sin(x)-4sin
3(x) berechnen, mit der Lösungsformel für kubische Gleichungen erhält man \(sin(\frac{\pi}{9})=2^{-\frac{4}{3}}(\sqrt[3]{i-\sqrt{3}}-\sqrt[3]{i+\sqrt{3}})\). Wie man daraus die Formel mit den vielen
8 bekommt... der Grenzwert der auf der linken Seite stehenden Folge ist eine Lösung von \(\sqrt{8-\sqrt{8+x}}=x \), äquivalent von \(x^4-16x^2-x+56=0\) und ich nehme mal an, dass sich dann durch Einsetzen die Gleichheit bestätigt (habe es aber nicht nachgerechnet).
Bei der
9 geht es um die fixpunktfreien Permutationen von 4 Elementen.
Die
14 zeigt das
Stomachion, ein Puzzle, das sich auf sehr viele verschiedene Weisen zu einem Quadrat zusammensetzen läßt.
Eine Smith-Zahl ist eine zusammengesetzte Zahl, bei der die Summe ihrer Ziffern gleich der Summe aller Ziffern ihrer Primfaktoren ist. Nach der 4 ist die
22 die zweitkleinste.
Die verschiedenen Ramsey-Zahlen R(r,b) bei
6, 25, 28 sind jeweils die kleinsten Zahlen, so dass jeder vollständige Graph mit R(r,b) Knoten und blau/rot gefärbten Kanten entweder einen roten r-Teilgraphen oder einen blauen b-Teilgraphen enthält.
 Der Eintrag bei der 1 zeigt den Graphen von \(f(x)=x^x\), der sein Minimum in 1/e hat und für x->0 gegen 1 strebt, was man zum Beispiel mittels der Substitution x=1/n aus \(\lim_{n\to\infty}\sqrt[n]{n}=1\) oder auch aus \(\lim_{n\to\infty}\frac{\ln(n)}{n}=0\) herleiten kann.
Der Eintrag bei der 2 zeigt die Eulersche Polyederformel: für einen konvexen Polyeder mit V Ecken, E Kanten und F Flächen hat man V-E+F=2. Mit heutiger Mathematik läßt sich das so begründen, dass konvexe Polyeder homöomorph zur Sphäre sind und die Euler-Charakteristik der Sphäre 2 ist. Siehe TvF 4.
Der Eintrag bei der 3 bezieht sich auf das 1796 von Gauss bewiesene Eureka-Theorem, demzufolge sich jede natürliche Zahl als Summe dreier Dreieckszahlen zerlegen läßt, eine der vielen unbewiesenen Vermutungen von Pierre de Fermat.
Der vollständige Graph auf 5 Ecken (Bild unten) läßt sich nicht kreuzungsfrei in die Ebene einbetten, beweisen kann man das zum Beispiel mit der Euler-Charakteristik.
Den Sinus von pi/9 kann man im Prinzip mittels der trigonometrischen Identität sin(3x)=3sin(x)-4sin3(x) berechnen, mit der Lösungsformel für kubische Gleichungen erhält man \(sin(\frac{\pi}{9})=2^{-\frac{4}{3}}(\sqrt[3]{i-\sqrt{3}}-\sqrt[3]{i+\sqrt{3}})\). Wie man daraus die Formel mit den vielen 8 bekommt... der Grenzwert der auf der linken Seite stehenden Folge ist eine Lösung von \(\sqrt{8-\sqrt{8+x}}=x \), äquivalent von \(x^4-16x^2-x+56=0\) und ich nehme mal an, dass sich dann durch Einsetzen die Gleichheit bestätigt (habe es aber nicht nachgerechnet).
Bei der 9 geht es um die fixpunktfreien Permutationen von 4 Elementen.
Die 14 zeigt das Stomachion, ein Puzzle, das sich auf sehr viele verschiedene Weisen zu einem Quadrat zusammensetzen läßt.
Eine Smith-Zahl ist eine zusammengesetzte Zahl, bei der die Summe ihrer Ziffern gleich der Summe aller Ziffern ihrer Primfaktoren ist. Nach der 4 ist die 22 die zweitkleinste.
Die verschiedenen Ramsey-Zahlen R(r,b) bei 6, 25, 28 sind jeweils die kleinsten Zahlen, so dass jeder vollständige Graph mit R(r,b) Knoten und blau/rot gefärbten Kanten entweder einen roten r-Teilgraphen oder einen blauen b-Teilgraphen enthält.
Der Eintrag bei der 1 zeigt den Graphen von \(f(x)=x^x\), der sein Minimum in 1/e hat und für x->0 gegen 1 strebt, was man zum Beispiel mittels der Substitution x=1/n aus \(\lim_{n\to\infty}\sqrt[n]{n}=1\) oder auch aus \(\lim_{n\to\infty}\frac{\ln(n)}{n}=0\) herleiten kann.
Der Eintrag bei der 2 zeigt die Eulersche Polyederformel: für einen konvexen Polyeder mit V Ecken, E Kanten und F Flächen hat man V-E+F=2. Mit heutiger Mathematik läßt sich das so begründen, dass konvexe Polyeder homöomorph zur Sphäre sind und die Euler-Charakteristik der Sphäre 2 ist. Siehe TvF 4.
Der Eintrag bei der 3 bezieht sich auf das 1796 von Gauss bewiesene Eureka-Theorem, demzufolge sich jede natürliche Zahl als Summe dreier Dreieckszahlen zerlegen läßt, eine der vielen unbewiesenen Vermutungen von Pierre de Fermat.
Der vollständige Graph auf 5 Ecken (Bild unten) läßt sich nicht kreuzungsfrei in die Ebene einbetten, beweisen kann man das zum Beispiel mit der Euler-Charakteristik.
Den Sinus von pi/9 kann man im Prinzip mittels der trigonometrischen Identität sin(3x)=3sin(x)-4sin3(x) berechnen, mit der Lösungsformel für kubische Gleichungen erhält man \(sin(\frac{\pi}{9})=2^{-\frac{4}{3}}(\sqrt[3]{i-\sqrt{3}}-\sqrt[3]{i+\sqrt{3}})\). Wie man daraus die Formel mit den vielen 8 bekommt... der Grenzwert der auf der linken Seite stehenden Folge ist eine Lösung von \(\sqrt{8-\sqrt{8+x}}=x \), äquivalent von \(x^4-16x^2-x+56=0\) und ich nehme mal an, dass sich dann durch Einsetzen die Gleichheit bestätigt (habe es aber nicht nachgerechnet).
Bei der 9 geht es um die fixpunktfreien Permutationen von 4 Elementen.
Die 14 zeigt das Stomachion, ein Puzzle, das sich auf sehr viele verschiedene Weisen zu einem Quadrat zusammensetzen läßt.
Eine Smith-Zahl ist eine zusammengesetzte Zahl, bei der die Summe ihrer Ziffern gleich der Summe aller Ziffern ihrer Primfaktoren ist. Nach der 4 ist die 22 die zweitkleinste.
Die verschiedenen Ramsey-Zahlen R(r,b) bei 6, 25, 28 sind jeweils die kleinsten Zahlen, so dass jeder vollständige Graph mit R(r,b) Knoten und blau/rot gefärbten Kanten entweder einen roten r-Teilgraphen oder einen blauen b-Teilgraphen enthält.




