Die Graphentheorie entwickelte sich seit Ende des 19. Jahrhunderts aus dem klassischen Vier-Farben-Problem. Dieses ist ein spezieller Fall des allgemeinen Problems, die Knoten eines Graphen so zu färben, dass durch eine Kante verbundene Knoten jeweils mit unterschiedlichen Farben gefärbt sind. Die Anzahl der Möglichkeiten, einen gegebenen Graphen G so mit n Farben zu färben, bezeichnet man mit P
G(n).
George Birkhoff gab 1912 ein rekursives Verfahren zur Berechnung von P
G(n): für einen Graphen G und eine Kante e seien G\e und G/e die Graphen, die man durch Entfernen bzw. Kontraktion der Kante e bekommt, dann ist P
G(n) die Differenz der entsprechenden Werte für die Graphen G\e und G/e.
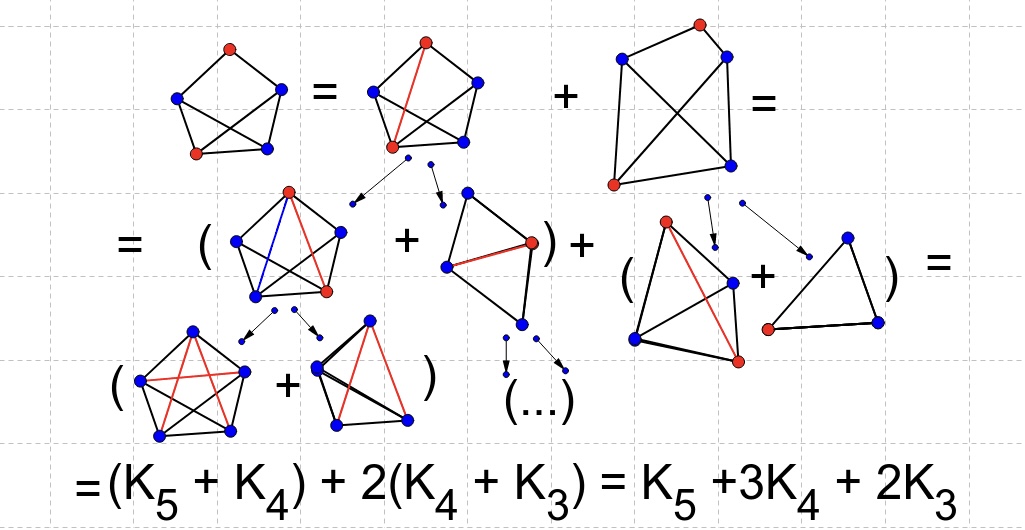
Mit dieser Rekursionsformel konnte Birkhoff insbesondere für alle Graphen G beweisen, dass P
G(n) ein Polynom in n ist. Man nennt es das chromatische Polynom des Graphen.
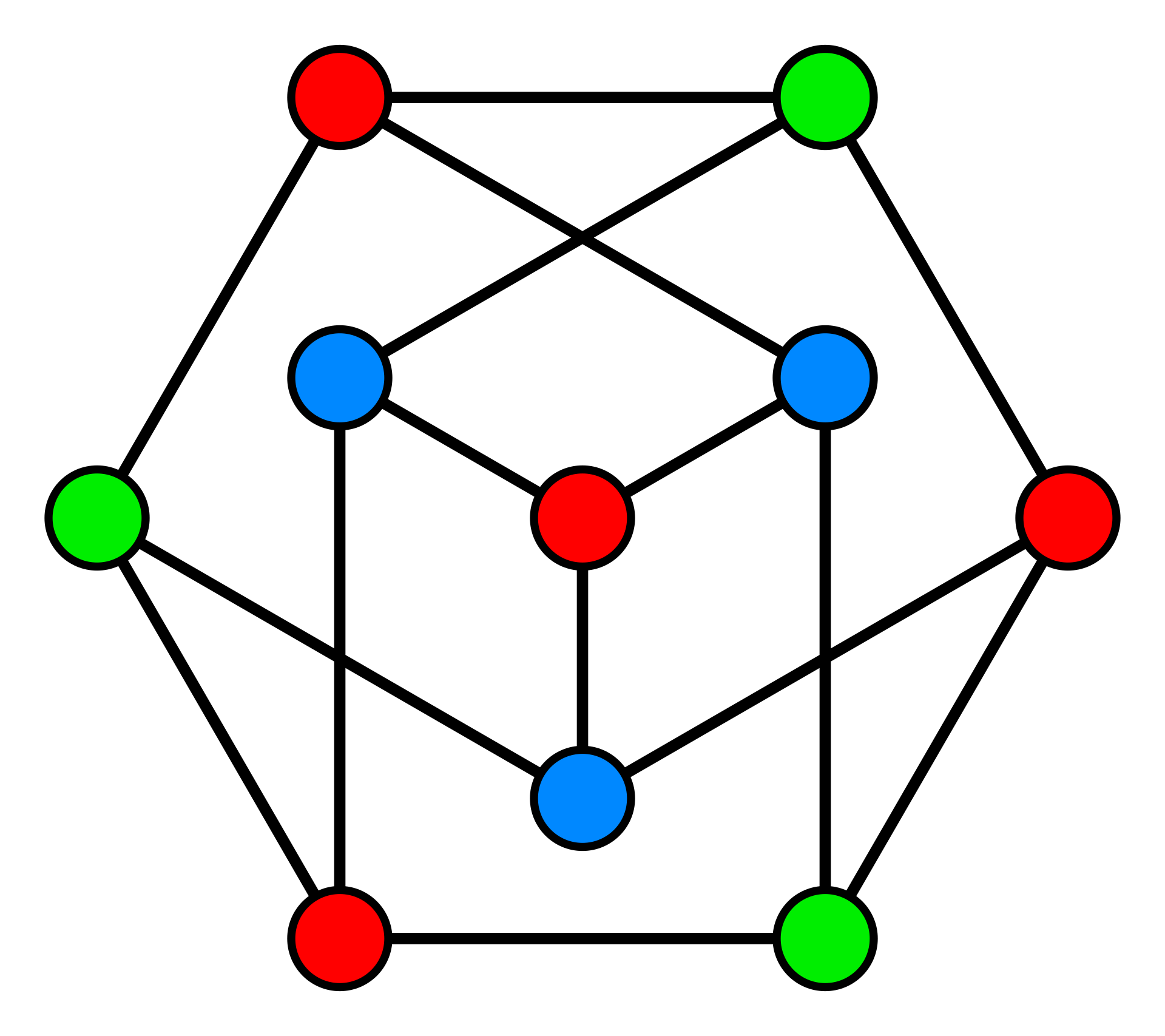
Das chromatische Polynom des oben abgebildeten Petersen-Graphen ist n
10-15n
9+104n
8-455n
7+1353n
6-2861n
5+4275n
4-4305n
3+2706n
2-704n. Zwei Eigenschaften dieses Polynoms, die sich (zunächst empirisch) auch für die chromatischen Polynome aller anderen Graphen verifizieren lassen, sind: die Vorzeichen alternieren, und die Folge der Koeffizienten ist unimodal, d.h. sie wächst zunächst und fällt dann.
Tatsächlich kann man die alternierenden Vorzeichen der Koeffizienten leicht per Induktion aus Birkhoffs Rekursionsformel beweisen. Dagegen war die zweite Eigenschaft, die Unimodalität der chromatischen Polynome aller Graphen, eine 1968 von Read aufgestellte und danach mehr als vierzig Jahre offene Vermutung.
Unimodalität hat man insbesondere für log-konkave Folgen ohne Nullen. Als log-konkav bezeichnet man Folgen, wo a
i-1a
i+1 ≤ a
i2 für alle i gilt. Der Name bezieht sich darauf, dass log(a
i) eine konkave Funktion ist. Für diese Folgen ist die Quotientenfolge a
i:a
i-1 monoton fallend, die Folge selbst also evtl. zunächst wachsend, aber wenn sie einmal zu fallen begonnen hat, dann weiterhin fallend, womit man die Unimodalität bewiesen hat. Log-konkave Folgen kommen in Algebra, Geometrie und vor allem Kombinatorik in vielen Zusammenhängen vor. Einfachstes Beispiel sind die Binomialkoeffizienten. Ein anderes bekanntes Beispiel sind die Alexandrov-Fenchel-Ungleichungen, denenzufolge die gemischten Volumina zweier konvexer Körper eine log-konkave Folge bilden. Rota, Heron und Welsh stellten eine allgemeinere Vermtutung auf, derzufolge die Koeffizienten des chromatischen Polynoms eine log-konkave Folge bilden und dies sogar allgemeiner für charakteristische Polynome von Matroiden gelten sollte.
Bewiesen wurde diese Vermutung 2011 von June Huh im ersten Jahr seines Promotionsstudiums, überraschenderweise mit Hilfe von Erkenntnissen aus der Singularitätentheorie. Tatsächlich hatte Huh die Vermutung nicht gekannt, sondern in seiner Beschäftigung mit Singularitäten und den zugehörigen Graphen dieses Muster gefunden, um anschließend bei der Literaturrecherche festzustellen, dass es in der Graphentheorie noch nicht bewiesen, sondern eine seit langem offene Vermutung war.
Die algebraische Geometrie kommt so ins Spiel: zu einem Graphen mit K Knoten betrachtet man ein Hyperebenenarrangement im
RK: wenn der i-te und j-te Knoten durch eine Kante verbunden sind, soll die Hyperebene x
i-x
j=0 zum Arrangement gehören.
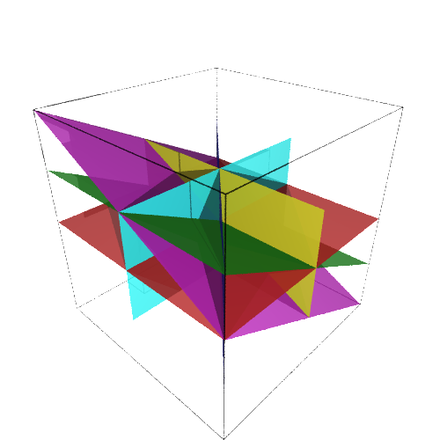
Das Komplement dieser Vereinigung von Hyperebenen bezeichnet man als Hyperebenenkomplement. Das chromatische Polynom des ursprünglichen Graphen läßt sich aus der Topologie des Hyperebenen-Komplements berechnen. Sei h(x
1,…,x
K) das Polynom, welches man als Produkt der Linearfaktoren x
i-x
j über alle Kanten (i,j) erhält. Dann ist D(h):={[x
1:...:x
K]: h(x
1,...,x
K)≠0} das Komplement des Hyperebenenarrangements im
CP
K-1 und aus einem damals schon bekannten Satz folgt, dass man aus den Betti-Zahlen b
i(D(h)) das chromatische Polynom berechnen kann: \(P_G(n)=(n-1)\sum_{i=0}^{K} (-1)^i b_i(D(h)) n^{K-i}\). Die Frage ist also, ob diese Betti-Zahlen eine log-konkave Folge bilden.
June Huh bewies, dass sich die Betti-Zahlen b
i (D(h)) mittels Singularitätentheorie berechnen lassen. Das Polynom h hat im Nullpunkt eine Singularität und man hat für solche Singularitäten eine gewisse von Milnor und Teissier untersuchte Invariante μ
i(h). Für homogene Polynome, die ein Produkt von Linearfaktoren sind (in diesem Fall aus den x
i-x
j), konnten Dimca und Papadima b
i(D(h)) mittels Morse-Theorie berechnen. Huh konstruierte damit eine CW-Zerlegung von D(h) in jeweils μ
i(h) i-Zellen.
Die Invariante μ
i(h) kann rein algebraisch definiert werden, sie ist die gemischte Vielfachheit \(e_i({\bf m},J_h)\) für das von den homogenen Elementen erzeugte "irrelevante Ideal" \({\bf m}\) und das Jacobi-Ideal J
h von h. In manchen Fällen stimmen diese gemischten Vielfachheiten mit gewissen gemischten Volumina von Gitterpolytopen überein, deren Log-Konkavität aus den Alexandrov-Fenchel-Ungleichungen der Konvexgeometrie bekannt ist. Mit Hilfe der Khovanskii-Teissier-Ungleichung konnte Huh dann auch unter sehr viel allgemeineren Annahmen die Log-Konkavität der \(e_i({\bf m},J_h)\) beweisen, während er Gegenbeispiele zu einer unter noch allgemeineren Annahmen von Trung und Verma formulierten Vermutung fand. Tatsächlich bewies er mit Hilfe der Khovanskii-Teissier-Ungleichung den folgenden Fakt für "Korrespondenzen", d.h. Homologieklassen \(\sum_i e_i\left[{\bf P}^{k-i}\times {\bf P}^i\right]\) in
Pnx
Pm: man kann genau dann ein Vielfaches dieser Homologieklasse durch eine irreduzible Untervarietät realisieren, wenn die e
i eine log-konkave Folge ohne Nullen bilden. Das läßt sich anwenden auf den Graphen des Ideals J
h und in diesem Fall stimmen die e
i mit \(e_i({\bf m},J_h)\) überein. Es folgt, dass die μ
i(h) eine log-konkave Folge bilden.
Mit demselben Argument konnte Huh auch Log-Konkavität der Koeffizienten des charakteristischen Polynoms für über
C (und damit dann allgemeiner über einem Körper der Charakteristik 0) realisierte Vektormatroide zeigen. Auch das war, wie der Reviewer in den
Mathematical Reviews bemerkte, nur eine sehr spezielle Konsequenz der sehr viel reichhaltigeren allgemeinen Resultate in seiner Arbeit.
 Mit dieser Rekursionsformel konnte Birkhoff insbesondere für alle Graphen G beweisen, dass PG(n) ein Polynom in n ist. Man nennt es das chromatische Polynom des Graphen.
Mit dieser Rekursionsformel konnte Birkhoff insbesondere für alle Graphen G beweisen, dass PG(n) ein Polynom in n ist. Man nennt es das chromatische Polynom des Graphen.
 Das chromatische Polynom des oben abgebildeten Petersen-Graphen ist n10-15n9+104n8-455n7+1353n6-2861n5+4275n4-4305n3+2706n2-704n. Zwei Eigenschaften dieses Polynoms, die sich (zunächst empirisch) auch für die chromatischen Polynome aller anderen Graphen verifizieren lassen, sind: die Vorzeichen alternieren, und die Folge der Koeffizienten ist unimodal, d.h. sie wächst zunächst und fällt dann.
Tatsächlich kann man die alternierenden Vorzeichen der Koeffizienten leicht per Induktion aus Birkhoffs Rekursionsformel beweisen. Dagegen war die zweite Eigenschaft, die Unimodalität der chromatischen Polynome aller Graphen, eine 1968 von Read aufgestellte und danach mehr als vierzig Jahre offene Vermutung.
Unimodalität hat man insbesondere für log-konkave Folgen ohne Nullen. Als log-konkav bezeichnet man Folgen, wo ai-1ai+1 ≤ ai2 für alle i gilt. Der Name bezieht sich darauf, dass log(ai) eine konkave Funktion ist. Für diese Folgen ist die Quotientenfolge ai:ai-1 monoton fallend, die Folge selbst also evtl. zunächst wachsend, aber wenn sie einmal zu fallen begonnen hat, dann weiterhin fallend, womit man die Unimodalität bewiesen hat. Log-konkave Folgen kommen in Algebra, Geometrie und vor allem Kombinatorik in vielen Zusammenhängen vor. Einfachstes Beispiel sind die Binomialkoeffizienten. Ein anderes bekanntes Beispiel sind die Alexandrov-Fenchel-Ungleichungen, denenzufolge die gemischten Volumina zweier konvexer Körper eine log-konkave Folge bilden. Rota, Heron und Welsh stellten eine allgemeinere Vermtutung auf, derzufolge die Koeffizienten des chromatischen Polynoms eine log-konkave Folge bilden und dies sogar allgemeiner für charakteristische Polynome von Matroiden gelten sollte.
Bewiesen wurde diese Vermutung 2011 von June Huh im ersten Jahr seines Promotionsstudiums, überraschenderweise mit Hilfe von Erkenntnissen aus der Singularitätentheorie. Tatsächlich hatte Huh die Vermutung nicht gekannt, sondern in seiner Beschäftigung mit Singularitäten und den zugehörigen Graphen dieses Muster gefunden, um anschließend bei der Literaturrecherche festzustellen, dass es in der Graphentheorie noch nicht bewiesen, sondern eine seit langem offene Vermutung war.
Die algebraische Geometrie kommt so ins Spiel: zu einem Graphen mit K Knoten betrachtet man ein Hyperebenenarrangement im RK: wenn der i-te und j-te Knoten durch eine Kante verbunden sind, soll die Hyperebene xi-xj=0 zum Arrangement gehören.
Das chromatische Polynom des oben abgebildeten Petersen-Graphen ist n10-15n9+104n8-455n7+1353n6-2861n5+4275n4-4305n3+2706n2-704n. Zwei Eigenschaften dieses Polynoms, die sich (zunächst empirisch) auch für die chromatischen Polynome aller anderen Graphen verifizieren lassen, sind: die Vorzeichen alternieren, und die Folge der Koeffizienten ist unimodal, d.h. sie wächst zunächst und fällt dann.
Tatsächlich kann man die alternierenden Vorzeichen der Koeffizienten leicht per Induktion aus Birkhoffs Rekursionsformel beweisen. Dagegen war die zweite Eigenschaft, die Unimodalität der chromatischen Polynome aller Graphen, eine 1968 von Read aufgestellte und danach mehr als vierzig Jahre offene Vermutung.
Unimodalität hat man insbesondere für log-konkave Folgen ohne Nullen. Als log-konkav bezeichnet man Folgen, wo ai-1ai+1 ≤ ai2 für alle i gilt. Der Name bezieht sich darauf, dass log(ai) eine konkave Funktion ist. Für diese Folgen ist die Quotientenfolge ai:ai-1 monoton fallend, die Folge selbst also evtl. zunächst wachsend, aber wenn sie einmal zu fallen begonnen hat, dann weiterhin fallend, womit man die Unimodalität bewiesen hat. Log-konkave Folgen kommen in Algebra, Geometrie und vor allem Kombinatorik in vielen Zusammenhängen vor. Einfachstes Beispiel sind die Binomialkoeffizienten. Ein anderes bekanntes Beispiel sind die Alexandrov-Fenchel-Ungleichungen, denenzufolge die gemischten Volumina zweier konvexer Körper eine log-konkave Folge bilden. Rota, Heron und Welsh stellten eine allgemeinere Vermtutung auf, derzufolge die Koeffizienten des chromatischen Polynoms eine log-konkave Folge bilden und dies sogar allgemeiner für charakteristische Polynome von Matroiden gelten sollte.
Bewiesen wurde diese Vermutung 2011 von June Huh im ersten Jahr seines Promotionsstudiums, überraschenderweise mit Hilfe von Erkenntnissen aus der Singularitätentheorie. Tatsächlich hatte Huh die Vermutung nicht gekannt, sondern in seiner Beschäftigung mit Singularitäten und den zugehörigen Graphen dieses Muster gefunden, um anschließend bei der Literaturrecherche festzustellen, dass es in der Graphentheorie noch nicht bewiesen, sondern eine seit langem offene Vermutung war.
Die algebraische Geometrie kommt so ins Spiel: zu einem Graphen mit K Knoten betrachtet man ein Hyperebenenarrangement im RK: wenn der i-te und j-te Knoten durch eine Kante verbunden sind, soll die Hyperebene xi-xj=0 zum Arrangement gehören.
 Das Komplement dieser Vereinigung von Hyperebenen bezeichnet man als Hyperebenenkomplement. Das chromatische Polynom des ursprünglichen Graphen läßt sich aus der Topologie des Hyperebenen-Komplements berechnen. Sei h(x1,…,xK) das Polynom, welches man als Produkt der Linearfaktoren xi-xj über alle Kanten (i,j) erhält. Dann ist D(h):={[x1:...:xK]: h(x1,...,xK)≠0} das Komplement des Hyperebenenarrangements im CPK-1 und aus einem damals schon bekannten Satz folgt, dass man aus den Betti-Zahlen bi(D(h)) das chromatische Polynom berechnen kann: \(P_G(n)=(n-1)\sum_{i=0}^{K} (-1)^i b_i(D(h)) n^{K-i}\). Die Frage ist also, ob diese Betti-Zahlen eine log-konkave Folge bilden.
June Huh bewies, dass sich die Betti-Zahlen bi (D(h)) mittels Singularitätentheorie berechnen lassen. Das Polynom h hat im Nullpunkt eine Singularität und man hat für solche Singularitäten eine gewisse von Milnor und Teissier untersuchte Invariante μi(h). Für homogene Polynome, die ein Produkt von Linearfaktoren sind (in diesem Fall aus den xi-xj), konnten Dimca und Papadima bi(D(h)) mittels Morse-Theorie berechnen. Huh konstruierte damit eine CW-Zerlegung von D(h) in jeweils μi(h) i-Zellen.
Die Invariante μi(h) kann rein algebraisch definiert werden, sie ist die gemischte Vielfachheit \(e_i({\bf m},J_h)\) für das von den homogenen Elementen erzeugte "irrelevante Ideal" \({\bf m}\) und das Jacobi-Ideal Jh von h. In manchen Fällen stimmen diese gemischten Vielfachheiten mit gewissen gemischten Volumina von Gitterpolytopen überein, deren Log-Konkavität aus den Alexandrov-Fenchel-Ungleichungen der Konvexgeometrie bekannt ist. Mit Hilfe der Khovanskii-Teissier-Ungleichung konnte Huh dann auch unter sehr viel allgemeineren Annahmen die Log-Konkavität der \(e_i({\bf m},J_h)\) beweisen, während er Gegenbeispiele zu einer unter noch allgemeineren Annahmen von Trung und Verma formulierten Vermutung fand. Tatsächlich bewies er mit Hilfe der Khovanskii-Teissier-Ungleichung den folgenden Fakt für "Korrespondenzen", d.h. Homologieklassen \(\sum_i e_i\left[{\bf P}^{k-i}\times {\bf P}^i\right]\) in PnxPm: man kann genau dann ein Vielfaches dieser Homologieklasse durch eine irreduzible Untervarietät realisieren, wenn die ei eine log-konkave Folge ohne Nullen bilden. Das läßt sich anwenden auf den Graphen des Ideals Jh und in diesem Fall stimmen die ei mit \(e_i({\bf m},J_h)\) überein. Es folgt, dass die μi(h) eine log-konkave Folge bilden.
Mit demselben Argument konnte Huh auch Log-Konkavität der Koeffizienten des charakteristischen Polynoms für über C (und damit dann allgemeiner über einem Körper der Charakteristik 0) realisierte Vektormatroide zeigen. Auch das war, wie der Reviewer in den Mathematical Reviews bemerkte, nur eine sehr spezielle Konsequenz der sehr viel reichhaltigeren allgemeinen Resultate in seiner Arbeit.
Das Komplement dieser Vereinigung von Hyperebenen bezeichnet man als Hyperebenenkomplement. Das chromatische Polynom des ursprünglichen Graphen läßt sich aus der Topologie des Hyperebenen-Komplements berechnen. Sei h(x1,…,xK) das Polynom, welches man als Produkt der Linearfaktoren xi-xj über alle Kanten (i,j) erhält. Dann ist D(h):={[x1:...:xK]: h(x1,...,xK)≠0} das Komplement des Hyperebenenarrangements im CPK-1 und aus einem damals schon bekannten Satz folgt, dass man aus den Betti-Zahlen bi(D(h)) das chromatische Polynom berechnen kann: \(P_G(n)=(n-1)\sum_{i=0}^{K} (-1)^i b_i(D(h)) n^{K-i}\). Die Frage ist also, ob diese Betti-Zahlen eine log-konkave Folge bilden.
June Huh bewies, dass sich die Betti-Zahlen bi (D(h)) mittels Singularitätentheorie berechnen lassen. Das Polynom h hat im Nullpunkt eine Singularität und man hat für solche Singularitäten eine gewisse von Milnor und Teissier untersuchte Invariante μi(h). Für homogene Polynome, die ein Produkt von Linearfaktoren sind (in diesem Fall aus den xi-xj), konnten Dimca und Papadima bi(D(h)) mittels Morse-Theorie berechnen. Huh konstruierte damit eine CW-Zerlegung von D(h) in jeweils μi(h) i-Zellen.
Die Invariante μi(h) kann rein algebraisch definiert werden, sie ist die gemischte Vielfachheit \(e_i({\bf m},J_h)\) für das von den homogenen Elementen erzeugte "irrelevante Ideal" \({\bf m}\) und das Jacobi-Ideal Jh von h. In manchen Fällen stimmen diese gemischten Vielfachheiten mit gewissen gemischten Volumina von Gitterpolytopen überein, deren Log-Konkavität aus den Alexandrov-Fenchel-Ungleichungen der Konvexgeometrie bekannt ist. Mit Hilfe der Khovanskii-Teissier-Ungleichung konnte Huh dann auch unter sehr viel allgemeineren Annahmen die Log-Konkavität der \(e_i({\bf m},J_h)\) beweisen, während er Gegenbeispiele zu einer unter noch allgemeineren Annahmen von Trung und Verma formulierten Vermutung fand. Tatsächlich bewies er mit Hilfe der Khovanskii-Teissier-Ungleichung den folgenden Fakt für "Korrespondenzen", d.h. Homologieklassen \(\sum_i e_i\left[{\bf P}^{k-i}\times {\bf P}^i\right]\) in PnxPm: man kann genau dann ein Vielfaches dieser Homologieklasse durch eine irreduzible Untervarietät realisieren, wenn die ei eine log-konkave Folge ohne Nullen bilden. Das läßt sich anwenden auf den Graphen des Ideals Jh und in diesem Fall stimmen die ei mit \(e_i({\bf m},J_h)\) überein. Es folgt, dass die μi(h) eine log-konkave Folge bilden.
Mit demselben Argument konnte Huh auch Log-Konkavität der Koeffizienten des charakteristischen Polynoms für über C (und damit dann allgemeiner über einem Körper der Charakteristik 0) realisierte Vektormatroide zeigen. Auch das war, wie der Reviewer in den Mathematical Reviews bemerkte, nur eine sehr spezielle Konsequenz der sehr viel reichhaltigeren allgemeinen Resultate in seiner Arbeit. 

