Wenn man die Entwicklung der Inzidenzen in unterschiedlichen Teilen Deutschlands betrachtet, dann fällt eine gewisse Periodizität auf: Gegenden, in denen die Inzidenz besonders hoch war, haben dann auch mal wieder besonders niedrige Inzidenzen und umgekehrt. Aktuell hat etwa Bremen, wo aus plausiblen Gründen die Inzidenz lange niedrig war, hohe Inzidenzen. Umgekehrt hat Thüringen mit seinen vielen Impfverweigerern aktuell gerade besonders niedrige Inzidenzen, nachdem es lange mit an der Spitze der Inzidenzzahlen gelegen hatte. In der Mathematik kennt man solche Phänomene auch aus anderen Bereichen, und sie lassen sich oft mit der Periodizität der Lotka-Volterra-Gleichungen erklären. Eine solche Erklärung der Entwicklung der Covid19-Pandemie mit den Lotka-Volterra-Gleichungen versucht die Arbeit “An analytical study of the dynamic behavior of Lotka-Volterra based models of COVID-19” von Wael W. Mohammed, E.S. Aly, A.E. Matouk, S. Albosaily und E.M. Elabbasye (Link).
Populationsdynamik und Lotka-Volterra-Gleichungen
Alfred Lotka, 1880 in Lemberg geboren, Chemie-Student in Leipzig und seit 1902 in den USA lebend, galt mit seinen Arbeiten über Altersverteilung und Geburts- und Sterbedaten als Begründer der mathematischen Demografie, seit 1924 arbeitete er bei der Metropolitan Life Insurance Company in New York. Die "Elements of Physical Biology" sollten sein Hauptwerk werden, mit ihm wollte er physikalische Prinzipien auf biologische Systeme übertragen, die gesamte belebte wie unbelebte Natur als ein Energieumwandlungssystem verstehen. Bekannt wurde vor allem seine mathematische Formulierung von Gesetzen der Populationsdynamik. Unabhängig von ihm stieß auch Vito Volterra auf dieselben populationsdynamischen Gesetze und dasselbe System von Differentialgleichungen. (Volterra, damals bereits 66 Jahre alt, hatte zuvor wesentliche Beiträge zur Theorie der Integralgleichungen und zahlreichen anderen Gebieten der Mathematik geleistet. Fünf Jahre später würde er in Rom entlassen werden, weil er den Eid auf die faschistische Regierung verweigerte.)
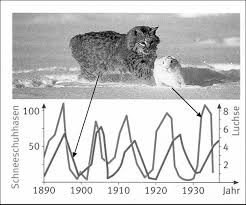
In ihrem Modell ging es um die Dynamik eines ökologischen Systems, in dem eine Raubtiergattung und seine Beute leben. Das emblematische Beispiel sind Luchse und Schneehasen, die Hudson's Bay Society hatte zu diesen beiden Arten genaue Zählungen seit dem vergangenen Jahrhundert vorliegen. (Volterra war durch den Biologen D’Ancona zu seiner Arbeit angeregt worden, der die Entwicklung von Raub- und Beutefischpopulationen in der Adria untersucht hatte.) Das Modell besteht aus zwei Differentialgleichungen, die die Entwicklung der Populationen jedes Tieres widerspiegeln:
\(x^\prime =x(a-by), y^\prime=y(-c+dx)\)
,wobei x und y die Anzahl der Räuber- und Beutetiere sind und die anderen (positiven) Parameter von den Rahmenbedingungen abhängen. Diese Differentialgleichungen modellierten die drei von beiden postulierten (und von Volterra mathematisch rigoros aus den Gleichungen hergeleiteten) Entwicklungsgesetze: - Die Populationsgrößen von Räuber und Beute schwanken periodisch. Dabei folgen die Schwankungen der Räuberpopulation phasenverzögert denen der Beutepopulation. Die Länge der Perioden hängt von den Anfangsbedingungen und von den Wachstumsraten der Populationen ab. - Die über genügend lange Zeiträume gemittelten Größen (Mittelwert) der Räuber- bzw. Beutepopulation sind konstant. Die Größe der Mittelwerte hängt nur von den Wachstums- und Rückgangsraten der Populationen, nicht aber von den Anfangsbedingungen ab. - Werden Räuber- und Beutepopulation gleichermaßen proportional zu ihrer Größe dezimiert, so vergrößert sich kurzfristig der Mittelwert der Beutepopulation, während der Mittelwert der Räuberpopulation kurzfristig sinkt. Alle drei Regeln gelten nur unter der Voraussetzung, dass lediglich zwischen den betrachteten beiden Arten eine Räuber-Beute-Beziehung besteht und die sonstigen biotischen und abiotischen Umweltfaktoren konstant oder zu vernachlässigen sind. Trotzdem waren sie in der praktischen Ökologie von großer Bedeutung.
Periodizität der Lotka-Volterra-Gleichungen
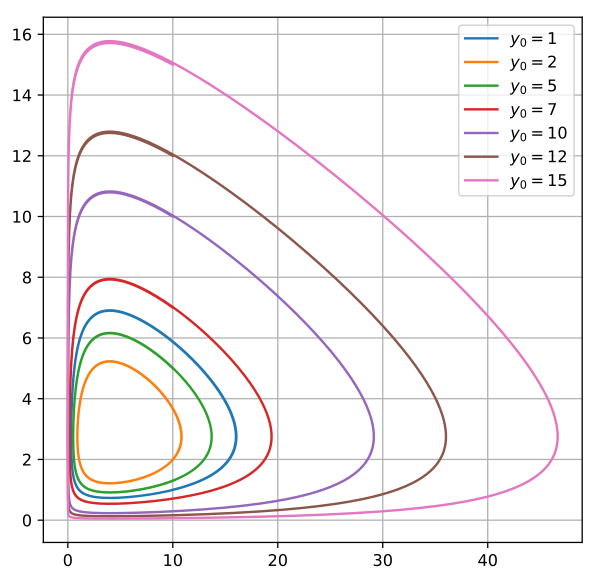
Mathematisch am interessantesten ist der Beweis der Periodizität, also dass sich die Lösungen wie im Bild in periodischen Bahnen um das Gleichgewicht (c/d,a/b) bewegen. Das sieht man am einfachsten mit der Hamilton-Funktion
\(c\ln(x)-dx+a\ln(y)-by \),
die eine Erhaltungsgrösse ist und deren Niveaumengen eben den Bahnen im Bild entsprechen. Man zeigt leicht, dass ihre Niveaumengen jede im Gleichgewicht startende Halbgerade in genau einem Punkt schneidet. Wenn man Polarkoordinaten \((r, \phi)\) mit dem Gleichgewicht \(( \frac{c}{d}, \frac{a}{b})\) als Ursprung betrachtet, kann man aus der Positivität der Parameter \(a,b,c,d\) die Ungleichung \(r^{2} \phi^{'}>0\) herleiten, womit die Bahn dann tatsächlich die gesamte geschlossene Kurve immer wieder durchlaufen muss - das beweist die Periodizität, die man bei Luchsen und Schneehasen auch in der Natur beobachten kann. Die Rechnung ist so einfach, dass wir sie hier vorführen können. Zunächst verschiebt man den Ursprung des Koordinatensystems in das Gleichgewicht \(( \frac{c}{d}, \frac{a}{b})\), betrachtet also Koordinaten
\(X=x-\frac{c}{d}, Y=y-\frac{a}{b}\).
Die Lotka-Volterra-Gleichungen transformieren sich dann in die Gleichungen
\(X^{'}=-b(X+\frac{c}{d})Y, Y^{'}=dX(Y+\frac{a}{b})\).
In Polarkoordinaten \(X=r \cdot cos \phi, Y=r \cdot sin \phi\) kann man dann auch X’ und Y’ in Polarkoordinaten ausdrücken und bekommt
\(r^2\varphi^{'}=XY^{' }- YX^{'} = dX^2Y + \frac{ad}{bX^{2}} + bXY^2 + \frac{bc}{dY^2} = dX^{2}(Y+\frac{a}{b}) + bY^{2}(X+\frac{c}{d}) = dX^{2}y + bY^{2}x\)
, was positiv ist. Also ist φ streng monoton wachsend. Bliebe φ beschränkt, dann müßte die Lösung gegen ein Gleichgewicht von φ konvergieren, das es aber wegen φ‘>0 nicht gibt. Also muß φ immer wieder zu einem gegebenen Wert zurückkehren.
Die ewige Wiederkehr
Die Periodizität der Lösungen der Lotka-Volterra-Gleichungen bedeutet, dass Luchse und Schneehasen in einem sich ewig wiederholenden Zyklus gefangen sind. Diese ewige Wiederkehr hatte bekanntlich schon Friedrich Nietzsche vorhergesagt mit dem Argument, dass die Zeit sich sowohl in die Vergangenheit als auch in die Zukunft unendlich ausdehne, die gesamte „Kraft“, Materie oder Energie, und folglich die Anzahl der möglichen „Kombinationen“ oder Zustände der Welt, aber endlich ist. Demzufolge müsse jeder mögliche Zustand der Welt bereits unendlich oft eingetreten sein und noch unendlich oft eintreten. Ungefähr gleichzeitig mit Nietzsche hatte Henri Poincaré den Wiederkehrsatz bewiesen, sozusagen eine schwächere Version der ewigen Wiederkehr: in einem Phasenraum endlichen Volumens kehrt für jede offene Umgebung U eines beliebigen Punktes x die Bahn von x unendlich oft nach \(U\) zurück. (Aber nicht unbedingt nach \(x\).) Der Beweis benutzt, dass der Hamiltonfluss auf dem Phasenraum volumen-erhaltend ist und er ist in heutiger Sprache eigentlich sehr einfach: bezeichne \(U_{wk}\) die nach \(U\) irgendwann zurückkehrenden Punkten, sei \(T\) die Zeit-1-Abbildung des Hamiltonflusses - also \(T(x(t))=x(t+1)\) - und sei
\(A=U\cup T^{-1}U\cup T^{-2}U\cup T^{-3}U\cup\ldots \).
Dann sind die nicht zurückkehrenden Punkte gerade die aus \(AT^{-1}A\). Weil \(T\) volumen-erhaltend und \(T^{-1}A\) eine Teilmenge von \(A\) ist, ist \(vol(AT^{-1}A)=0\), also sind die nicht zurückkehrenden Punkte eine Nullmenge und \(vol(U_{wk})=vol(U)\). Poincaré konnte den Beweis nicht so einfach formulieren, weil man damals das Lebesgue-Maß und überhaupt die Sprache von Maßtheorie und Topologie noch nicht hatte. Bemerkenswerterweise ist der Beweis des Wiederkehrsatzes eigentlich nur eine mathematische Ausformulierung von Nietzsches Argument. Die numerisch berechnete Wiederkehrzeit realer physikalischer Systeme liegt allerdings weit über dem vermuteten Alter des Universums.
Ewige Wiederkehr des Konjunkturzyklus?
Eine “Anwendung” der Lotka-Volterra-Gleichungen in der Ökonomie ist das Goodwin-Modell des Konjunkturzyklus, das in den 60er Jahren von Richard Goodwin entwickelt und seit den 70er Jahren von einigen marxistischen Wirtschaftswissenschaftlern propagiert wurde. Die Variablen sind hier die Beschäftigungsquote und die Lohnquote. Für diese sollen die Lotka-Volterra-Gleichungen gelten, woraus dann also rein mathematisch die Periodizität der Bahnen folgt. Wenn man sich allerdings die reale Entwicklung von Lohn- und Beschäftigungsquote anschaut, dann ist diese keineswegs periodisch. Das Bild unten (aus der Wikipedia) zeigt die Entwicklung der Beschäftigungsquote und Lohnquote in Deutschland von 1991 bis 2015. Der rote Punkt zeigt den Stand im Frühling 1991, danach wird alle drei Monate ein weiterer Punkt eingetragen. Während man für die 90er Jahre tatsächlich eine Zykelbewegung ausmachen kann, hat man seit 2005 ein stetes Ansteigen der Beschäftigungsquote unabhängig vom Steigen oder Fallen der Lohnquote. Einzelne Ausschläge kann man leicht mit damals aktuellen Ereignissen in Verbindung bringen.
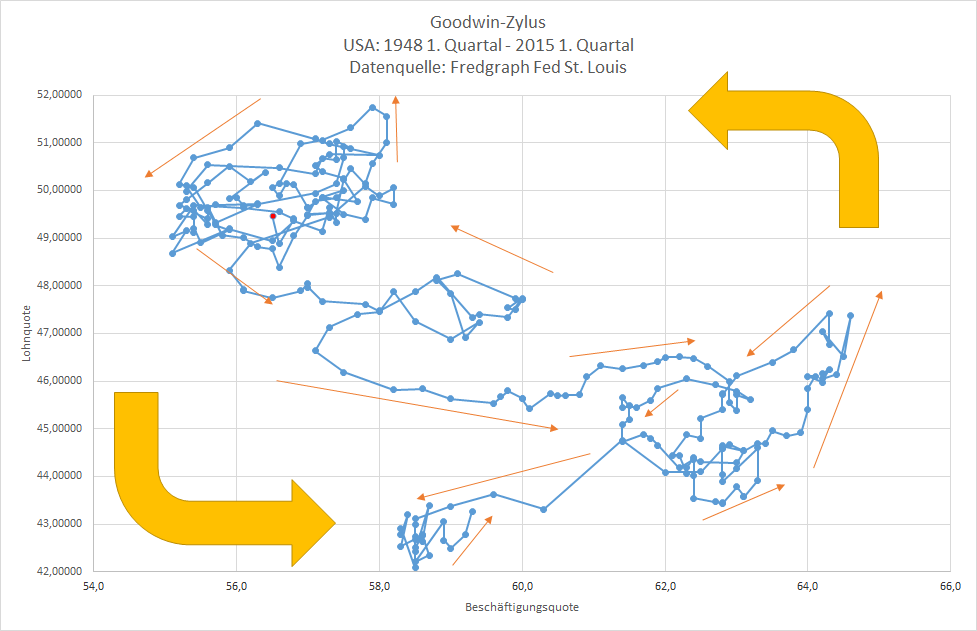
Noch instruktiver ist vielleicht ein Blick auf die entsprechenden Daten der USA von 1948 bis 2015 im Bild unten (ebenfalls aus der Wikipedia). Man sieht dort zwar tatsächlich zahlreiche Zykel, aber stets nur für einen begrenzten Zeitraum. Dazwischen gibt es immer wieder größere Ausschläge, nach denen man zwar letztlich wieder in eine periodische Bewegung hineinkommt, die aber nicht mit dem vorherigen Zykel übereinstimmt. Langfristig kann von einer Zykelbewegung keine Rede sein.
Zumindest für die letzten siebzig Jahre hat man also keine ewige Wiederkehr. Tatsächlich ist auch bei den Luchsen und Schneehasen die Übereinstimmung der Daten mit dem Modell der Lotka-Volterra-Gleichungen durchaus umstritten. “Do hares eat lynx?” fragte deshalb Michael Gilpin in einer 1973 veröffentlichten Arbeit. In der eingangs erwähnten Arbeit “An analytical study of the dynamic behavior of Lotka-Volterra based models of COVID-19” von Mohammed et al. werden nun Virus und Mensch als Räuber- und Beutetier angenommen und es werden aber noch die Mutationen des Virus berücksichtigt. Man hat jetzt fünf positive Parameter \(a,b,c,d,e\) und betrachtet das Differentialgleichungssystem
\(x^{'}=ax-bxy+ey, y^{'}=bxy+(c-d-e)y\).
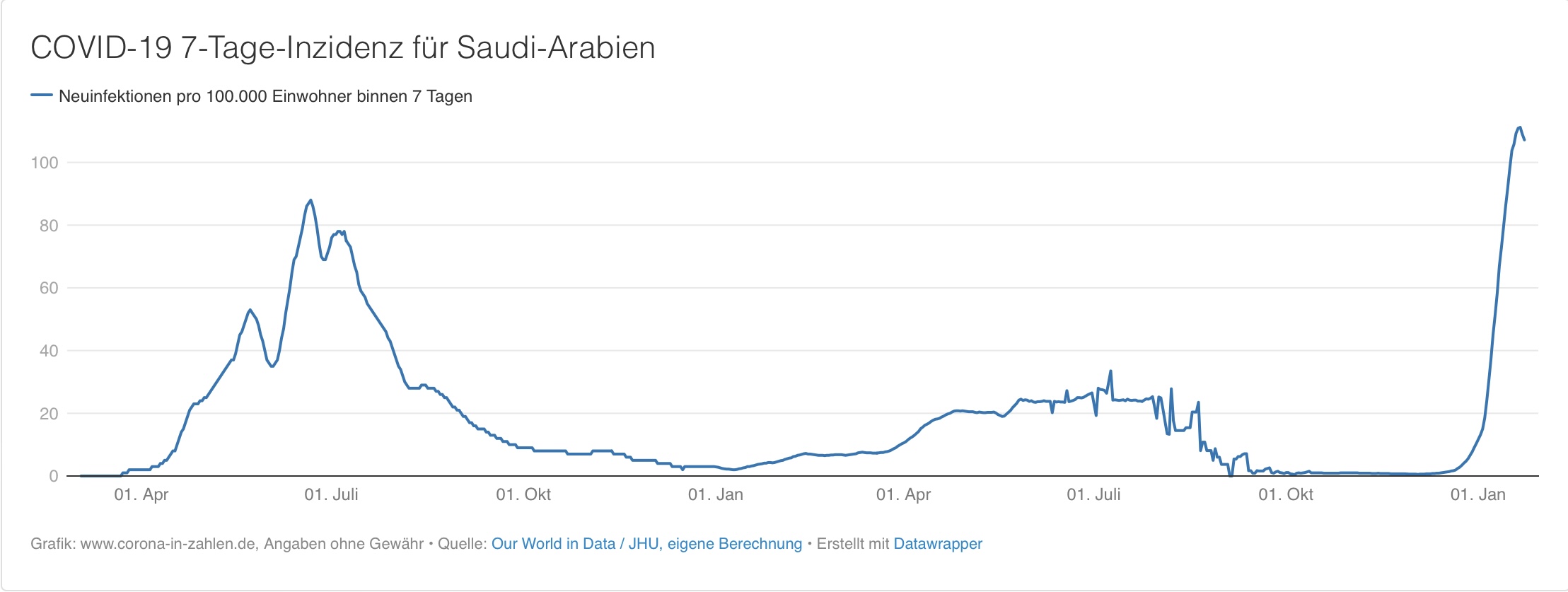
Dieses System hat ein Gleichgewicht in \(( \frac{e+d-c}{b}, a\frac{(e+d-c)}{b(d-c)})\). Lösungen bleiben beschränkt, das Gleichgewicht ist aber nur unter gewissen Voraussetzungen an die Parameter stabil. Im Fall von Saudi-Arbeiten berechnen die Autoren aus den bekannten Daten die Parameter a,b,c,d,e und zeigen mittels numerischer Berechnungen, dass in diesem Fall eine sehr schnelle Konvergenz gegen das Gleichgewicht erfolgen sollte. Die Arbeit wurde im Juli 2021 veröffentlicht. Die unten abgebildete weitere Entwicklung der Covid19-Pandemie in Saudi-Arabien sieht für mich aber nicht nach Konvergenz gegen ein Gleichgewicht aus.
Offene Fragen
Man kann übrigens auch bei drei sich gegenseitig fressenden Tierarten ein Differentialgleichungssystem vom Lotka-Volterra-Typ aufstellen, dann in 3 Variablen. In diesem Fall sind nicht alle Bahnen periodisch, man hat aber Grenzzyklen (periodische Bahnen, gegen die andere nichtperiodische Bahnen konvergieren). Es ist eine offene Frage, ob es dreidimensionale Lotka-Volterra-Gleichungen mit mehr als drei Grenzzykeln gibt. Man kann das als Spezialfall einer Verallgemeinerung von Hilberts 16. Problem sehen, das ja nach der Anzahl von Grenzzykeln für (zweidimensionale) Differentialgleichungssysteme mit polynomieller rechter Seite fragt.