It’s really beautiful to observe, as you progress in your mathematical maturity, how everything is somehow connected. (Sylvia Serfaty in "The Beauty of Mathematics: It Can Never Lie to You", Wired, März 2017)
Kein ICM
Der International Congress of Mathematicians, der alle vier Jahre stattfindende Weltkongreß der Mathematiker, sollte 2022 bekanntlich vom 6.-14. Juli in St. Petersburg stattfinden, was wegen zahlreicher Boykottdrohungen letztlich nicht realisiert wurde. Weil sich so kurzfristig kein anderer Veranstaltungsort organisieren ließ, wurde der Kongreß dann im Internet veranstaltet, was zweifellos einen enormen organisatorischen Aufwand bedeutete. Ein positiver Effekt war, dass nun jeder kostenlos und ohne Reisekosten dort teilnehmen konnte, man mußte sich nur registrieren. Offensichtlich wollten das auch viele, die Teilnehmerzahl übertraf die Erwartungen: obwohl es keinen Anmeldeschluß gab, war die Anmeldung wegen der hohen Nachfrage bald geschlossen. Wer sich rechtzeitig angemeldet hatte, bekam seit dem Abend des 3. Juli die abgebildete Begrüßungsseite zu sehen. Eigentlich kam es dann aber nicht darauf an, angemeldet zu sein, weil die Vorträge auch auf YouTube übertragen und gespeichert wurden. 
Tatsächlich hatten viele der Vorträge vor einem Life-Publikum stattgefunden, weil sich Vortragende zusammengetan hatten, um an einem Ort mit größerem Publikum jeweils ihre Vorträge zu halten. So fanden etwa Vorträge zu Zahlentheorie und algebraischer Geometrie in Zürich statt, Vorträge zu Geometrie, Topologie und verwandten Gebieten in Kopenhagen, Vorträge zu Dynamik in Jerusalem, zu Wahrscheinlichkeit und mathematischer Physik in Helsinki, zu angewandter Mathematik in London und zu Lie-Theorie in Singapur. Während des ICM wurden dann in der Regel die vorproduzierten Videos abgespielt, was den Vortragenden die (freilich kaum genutzte) Möglichkeit gab, während des Vortrags Fragen auf Discord zu beantworten. In einigen Fällen hatten Vortragende mit großem Aufwand Videos an verschiedenen Orten produziert. Frank Calegari sieht man während seines Vortrages abwechselnd in der Bibliothek, an der Tafel und auf dem heimischen Sofa. Es muß viel Arbeit (vermutlich mehrerer Leute) gewesen sein, das alles zu produzieren und zu schneiden. Calegari hatte schon am 27. Februar (also unmittelbar nach der Entscheidung für einen virtuellen ICM) auf seinem Blog „Persiflage“ gefragt: "What should a good ICM talk look like?"
So an ICM of zoom talks (on a St Petersburg schedule in the middle of the night in Chicago) does sound a little uninspiring. But what would be better? pre-recorded zoom lectures sound even worse. The idea of a polished video presentation has some appeal, but possibly it is also unrealistic. The sound and audio quality of a standard zoom lecture are OK if you are interested enough in the material, but I think one should expect a general ICM audience to be a little less forgiving. (Yes, plenty of people give terrible colloquia, but at least there are usually cookies.) And even with access to high quality audio and video, is it just going to be someone standing in front of their blackboard?
Während die Antworten im Blog nicht sehr ergiebig waren, hat er aber offenbar genug Ideen gehabt, um ein sehr ansprechendes Video zu produzieren, mit wechselndem Hintergrund und streckenweise unterlegt mit dramatisierender klassischer Musik. Das Resultat kann man auf https://youtu.be/L0Z4Ng6ZJbY ansehen. In nur 45 Minuten erhält man eine Einführung in die Entwicklungen der algebraischen Zahlentheorie der letzten 30 Jahre seit dem Beweis von Fermats letztem Theorem.
Fields-Medaillen
In den Tagen vor dem Kongreß fand in Helsinki die Generalversammlung der Internationalen Mathematischen Vereinigung statt. Sie entschied, dass der nächste ICM 2026 in Philadelphia, USA stattfinden soll. Der in New York ansässige Blog "Not even wrong" kommentierte:
With the 2022 experience in mind, hopefully the IMU will for next time have prepared a plan for what to do in case they again end up having a host country with a collapsed democracy being run by a dangerous autocrat.
Über die bis zum Kongreß geheimgehaltenen Gewinner der Fields-Medaillen wird immer schon Jahre zuvor auf verschiedenen Internetseiten spekuliert, insbesondere auf der Seite Economics Job Market Rumors, wo die Diskussion über mögliche Kandidaten für 2022 letztlich auf mehr als 1800 anonyme Beiträge angewachsen war, die oft erstaunliche Insider-Kenntnisse aus der Mathematik verrieten. Jedenfalls waren in diesem Jahr die meistgenannten Namen dann auch die tatsächlich in Helsinki verkündeten Preisträger: Maryna Viazovska für die Optimalität gewisser Kugelpackungen im 8- und 24-dimensionalen Raum (zweiteres mit Koautoren) und in weiteren Arbeiten (mit Koautoren) Grundlagen der harmonischen Analysis, von denen man sich noch viele Anwendungen erwartet, James Maynard für Verbesserungen der Abschätzungen für Primzahllücken und (mit Koukoulopoulos) den Beweis der Duffin-Schaeffer-Vermutung aus der diophantischen Approximation, Hugo Duminil-Copin für zahlreiche tiefe Sätze der Perkolationstheorie und über Gittermodelle der mathematischen Physik, und June Huh (der übrigens anders als in der medialen Berichterstattung korrekterweise Jun-i Ho mit kurzem "o" am Ende auszusprechen ist) für den Beweis der Unimodalität des chromatischen Polynoms von Graphen und (mit Koautoren) zahlreicher weiterer kombinatorischer Vermutungen.
Graphenfärbungen und Singularitätentheorie
Die Graphentheorie entwickelte sich seit Ende des 19. Jahrhunderts aus dem klassischen Vier-Farben-Problem. Dieses ist ein spezieller Fall des allgemeinen Problems, die Knoten eines Graphen so zu färben, dass durch eine Kante verbundene Knoten jeweils mit unterschiedlichen Farben eingefärbt sind. Die Anzahl der Möglichkeiten, einen gegebenen Graphen G so mit n Farben zu färben, bezeichnet man mit \(\chi_G(n)\). Das Vier-Farben-Problem ist also äquivalent zu der Frage, ob \(\chi(G, 4) \ge 1\) für alle ebenen Graphen G gilt. George Birkhoff gab 1912 ein rekursives Verfahren zur Berechnung von \(\chi_G(n)\): für einen Graphen G und eine Kante e seien G-e und G/e die Graphen, die man durch Entfernen bzw. Kontraktion der Kante e bekommt, dann ist \(\chi_G(n) = \chi_{G\setminus e}(n) - \chi_{G/e}(n)\). Mit dieser Formel kann man \(\chi(G, n)\) rekursiv berechnen und man kann per Induktion beweisen, dass \(\chi(G, n)\) ein Polynom in n ist, sein Grad ist die Anzahl der Knoten von G. Man nennt es das "chromatische Polynom" des Graphen. Birkhoff hoffte, mit Methoden zur Nullstellenbestimmung von Polynomen letztlich auch das Vier-Farben-Problem lösen zu können, was sich nicht erfüllte.
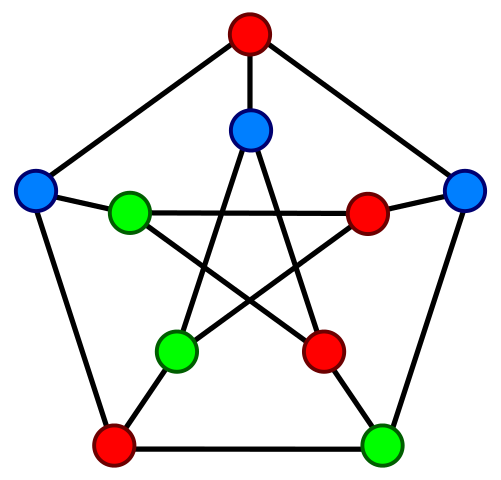
Das chromatische Polynom des oben abgebildeten Petersen-Graphen ist
\(n(n-1)(n-2)(n^7 - 12n^6 + 67n^5 - 230n^4 + 529n^3 - 814n^2 + 775n - 352)\\ = n^{10} - 15n^9 + 105n^8 - 455n^7 + 1353n^6 - 2861n^5 + 4305n^3 + 2606n^2 - 704n\)
Beim Betrachten dieses Polynoms fallen zwei Dinge auf:
- die Vorzeichen alternieren,
- die Folge der Koeffizienten wächst zunächst (in diesem Fall bis zum Koeffizienten von n3, bei anderen Graphen bis zu einer anderen Potenz) und fällt dann.
Folgen mit der zweiten Eigenschaft nennt man unimodal. Berechnet man charakteristische Polynome weiterer Graphen, so wird man feststellen, dass sie alle diese Eigenschaften haben. Zum Beispiel hat der vollständige Graph auf fünf Knoten K5 das chromatische Polynom
\(n(n-1)(n-2)(n-3)(n-4) = n^5 - 10n^4 + 35n^3 - 50n^2 + 24n\)
oder der bipartite Graph K2, 3 das chromatische Polynom
\( n(n-1)(n^3 - 5n^2 + 10n - 7) = n^5 - 6n^4 + 15n^3 - 17n^2 + 7n\).
Tatsächlich kann man die alternierenden Vorzeichen der Koeffizienten leicht per Induktion aus der Rekursionsformel beweisen. Dagegen war die zweite Eigenschaft, die Unimodalität der chromatischen Polynome von Graphen, eine seit 1968 offene Vermutung von Read. Beweisen wurde sie 2010 von June Huh, und zwar überraschenderweise mit Hilfe von Erkenntnissen aus der Singularitätentheorie, einem Teilgebiet der algebraischen Geometrie. Die algebraische Geometrie kommt so ins Spiel: zu einem Graphen mit K Knoten betrachtet man ein Hyperebenenarrangement im RK: wenn der i-te und j-te Knoten durch eine Kante verbunden sind, soll die Hyperebene \(x_i - x_j = 0\) zum Arrangement gehören.
Das chromatische Polynom des ursprünglichen Graphen läßt sich aus der Topologie des Hyperebenen-Komplements berechnen. Sei \(h(x_1, \ldots, x_K)\) das Polynom, welches man als Produkt der obigen Linearfaktoren xi - xj erhält. Dann ist \( D(h) := \left\{ \left[x_1: \ldots : x_K \right] \in {\bf C}P^{K-1} : h(x_1, \ldots, x_K) \neq 0 \right\}\) das Komplement des Hyperebenenarrangements. Seien \(b_i(D(h))\) seine Betti-Zahlen, also die Dimensionen der i-ten Homologiegruppen. Aus einem Satz von Orlik-Solomon folgt, dass \((n-1) \sum_ {i=0}^{K} (-1)^{i}b_{i}(D(h))n^{K-i} = \chi(G, n)\) das chromatische Polynom des Graphen G ist. Huh bewies dann, dass die Bettizahlen \(b_i(D(h))\) sich mittels Singularitätentheorie berechnen lassen. Allgemein sei h ein homogenes Polynom, welches ein Produkt aus linearen Faktoren ist (hier aus den \(x_i - x_j\)), dann kann man \(b_i(D(h))\) mittels Morse-Theorie berechnen und als Ergebnis erhält man die i-te Milnor-Zahl \(\mu_i(h)\) der Singularität, die das Polynom h im Nullpunkt hat. Diese ergibt sich rein algebraisch wie folgt. Betrachte die Ideale \(m = (x_1, \ldots, x_K), J = (\frac{\partial h}{\partial x_1}, \ldots, \frac{\partial h}{\partial x_K})\), dann ist die Dimension von \({\bf C} \left[x_1, \ldots, x_K\right]/m^uJ^v\) eine (polynomielle) Funktion in u und v und man erhält \(\mu_i (h)\) als \( (n-i)!i!\) mal den Koeffizienten von \( u^{n-i}v^i\) in \({\bf C}\left[x_1, \ldots, x_K\right]/m^uJ^v\). Und schließlich bewies er, dass (unter gewissen Voraussetzungen, die durch die spezielle Wahl der Polynome h hier erfüllt sind) die Milnor-Zahlen \(\mu_i(h)\) eine unimodale Folge bilden, woraus sich dann ergibt, dass auch die Koeffizienten des chromatischen Polynoms eine unimodale Folge bilden. (Dieser Beweis benutzte wiederum, dass die Milnor-Zahlen mit gewissen gemischten Volumina aus der Konvexgeometrie übereinstimmen, deren Unimodalität bekannt war.) Zweifellos eine überraschende Anwendung der algebraischen Geometrie in der Graphentheorie.
Die Standard-Vermutungen
In einer 2018 in den Annals of Mathematics erschienenen Arbeit von Adiprasito, Huh und Katz wurde dann gezeigt, dass dies ein Spezialfall eines allgemeineren Phänomens ist und allgemein für die charakteristischen Polynome sogenannter Matroide gilt. Hinter diesem allgemeinen Resultat steckt eine Struktur, die in allen möglichen Zusammenhängen in der Mathematik vorkommt und damit für viele in unterschiedlichen Zusammenhängen vorkommende unimodale Polynome verantwortlich ist: die sogenannten Lefschetz-Pakete. Seit den 40er Jahren galten die Weil-Vermutungen als die größte offene Frage der algebraischen Geometrie. Sie besagen, dass man die Anzahl der Lösungen einer polynomiellen Gleichung modulo einer Primzahlpotenz \(p^m\) bestimmen kann, wenn man die algebraische Topologie derselben Gleichung über den komplexen Zahlen (d.h. die Betti-Zahlen der entsprechenden Varietät im \({\bf C}P^n\)) kennt. Zum Beispiel ist es nicht einfach die Anzahl der Lösungen von \(x^3+y^3+z^3=0\) modulo einer Primzahlpotenz zu berechnen. Über den komplexen Zahlen ist diese Kurve in der projektiven Ebene aber einfach ein Torus. Die Betti-Zahlen sind \(b_0 = 1, b_1 = 2, b_2 = 1\). Mit den Weil-Vermutungen bekommt man dann zum Beispiel 9 Lösungen modulo 7, 63 Lösungen modulo 72, 324 Lösungen modulo 73 und eine allgemeine Formel für die Anzahl der Lösungen modulo \(7^m\). Alexander Grothendieck erkannte 1968, dass man die Weil-Vermutungen herleiten könnte, wenn es es eine Struktur aus Poincaré-Dualität, schwerem Lefschetz-Satz und Hodge-Riemann-Relationen auch auf den Chow-Gruppen (den Gruppen algebraischer Zykel modulo homologischer Äquivalenz in einer algebraischen Varietät) gibt. Die vermutete Existenz dieser Strukturen wurde dann als Standardvermutungen bekannt. Alexander Grothendiecks Zugang zur Mathematik war der eines Theoriebauers statt eines Problemlösers. Auch an den Weil-Vermutungen interessierte ihn nicht das schwere und berühmte Problem, sondern die zu suchende dahinterliegende versteckte Struktur. Erich Kähler hatte Anfang der 30er Jahre die Differentialgeometrie mit den Arbeiten der italienischen Schule zur algebraischen Geometrie verbinden wollen und in diesem Zusammenhang auf komplexen Mannigfaltigkeiten Riemannsche Metriken betrachtet, für die \(\omega = \sum g_{ij}dz^idz^j\) eine geschlossene 2-Form ist. Dies ist insbesondere für die Fubini-Study-Metrik auf Untermannigfaltigkeiten des \({\bf C}P^n\) der Fall, also auch für glatte projektive Varietäten. Für solche "Kähler-Mannigfaltigkeiten" funktioniert die von Lefschetz in den 20er Jahren für das Studium der Topologie algebraischer Varietäten entwickelte Maschinerie. In der Sprache der deRham-Kohomologie kann man sie so formulieren, dass für jedes k (und d die Dimension der Mannigfaltigkeit) das Cup-Produkt mit \(\omega^{d-2k}\) einen Isomorphismus \(H^k \to H^{d-k}\) gibt ("schwerer Satz von Lefschetz"), und man zusammen mit der Poincaré-Dualität \(H^k \to (H^{d-k})^*\) eine symmetrische Paarung \(H^k \times H^k \to H^d = {\bf R}\) erhält, die auf dem Kern von \(\omega^{d-2k+1}\) positiv definit ist. Ausgerechnet gibt diese positive Definitheit die sogenannten Hodge-Riemann-Relationen, die in der komplexen und algebraischen Geometrie an vielen Stellen verwendet werden. Spezieller hat man diese Strukturen dann auch auf der Dolbeault-Kohomologie \(H^{k, k}\).
Kähler hatte Ende der 50er Jahre auch versucht, Zahlentheorie und Geometrie zusammenbringen, indem er Varietäten über lokalen Ringen statt nur über Körpern betrachtete. Nach dem Erscheinen von Grothendiecks Arbeiten verfolgte er dieses Programm aber nicht weiter. Die Geometrie von Kähler-Mannigfaltigkeiten wurde jedoch zu einem wichtigen Ideengeber für die algebraische Geometrie. Die ursprünglich von Hodge für Kähler-Mannigfaltigkeiten entwickelte Theorie harmonischer Formen ließ sich durch Hironakas Auflösung der Singularitäten auch auf projektive Varietäten mit Singularitäten übertragen, was zu Delignes Theorie der gemischten Hodge-Strukturen führte. In einer anderen Richtung entwickelten Goresky und MacPherson eine sogenannte Schnittkohomologie für projektive Varietäten (mit Singularitäten), für die man analog zur Dolbeault-Kohomologie von Kähler-Mannigfaltigkeiten ebenfalls Poincaré-Dualität, den schweren Lefschetz-Satz und die Hodge-Riemann-Relationen hat. Mit den Standardvermutungen soll es ein solches Lefschetz-Paket dann auch auf den Chow-Gruppen algebraischer Varietäten geben. Damit wollte Grothendieck insbesondere zeigen, dass seine Kategorie der reinen Motive eine halbeinfache abelsche Kategorie ist und eine universelle Kohomologietheorie für Schemata gibt. Die Weil-Vermutungen ergäben sich daraus als Anwendung. Während für die Gültigkeit von Grothendiecks Standardvermutungen heute nicht viel mehr Fälle bekannt sind als 1968 (abelsche Varietäten, Fahnenvarietäten, verschiedene spezielle Beispiele), wurden die Weil-Vermutungen 1974 von Deligne bewiesen. Er benutzte statt der Standardvermutungen explizitere Methoden der Zahlentheorie wie Modulformen und neben den Methoden aus Grothendiecks Eléments de Géométrie Algébrique noch zahlreiche andere Ingredienzien wie einen von Kazhdan und Margulis bewiesenen Satz über die Monodromiegruppen von Lefschetz-Büscheln, eine Methode Rankins für Abschätzungen von Ramanujans Tau-Funktion, Arbeiten Grothendiecks über gewisse L-Funktionen, die klassische Invariantentheorie der symplektischen Gruppen, Spektralsequenzen und einen Trick, der mit Tensorpotenzen Abschätzungen beweist. Grothendieck beschwerte sich später in Récoltes et Semailles bitterlich, dass seine Arbeit von seinen Schülern nicht fortgesetzt worden sei und diese die Schwierigkeiten einfach "umgangen" hätten.
Säen und Ernten
Der New Yorker hatte im Mai einen Artikel "The Mysterious Disappearance of a Revolutionary Mathematician" von Rivka Galchen über Alexander Grothendieck. Mit zahlreichen Vergleichen, Geschichten und Veranschaulichungen wurde versucht, auch dem Laien das Revolutionäre an Grothendiecks Mathematik nahezubringen ohne in irgendwelche mathematischen Details zu gehen. Beispielsweise wurde sein funktorieller Zugang zur Mathematik mit einem Zitat von Angela Gibney so beschrieben
If you want to know about people, you don’t just look at them individually - you look at them at a family reunion.
Bereits im Januar war (nach mehr als 35 Jahren) Grothendiecks 1500-seitiges Spätwerk "Récoltes et Semailles" bei Gallimard erschienen, ein Buch über philosophische und das Überleben der Menschheit betreffende Fragen und auch über Mathematik und Mathematiker. Grothendieck beschreibt in diesem Buch seinen Weg und beklagt sich, dass Studenten und Kollegen seine Arbeit nicht fortgeführt, sondern mathematische Probleme auf andere Weise gelöst hätten. Zum Verständnis hilft es vielleicht, Teile der veröffentlichten Korrespondenz Grothendieck-Serre zu lesen. Die letzten Briefe dieser Korrespondenz datieren von 1986/87 und Serre schreibt dort (meine Übersetzung)
Irgendwo beschreibst Du Deinen Zugang zur Mathematik, bei dem man ein Problem nicht frontal angeht, sondern es in eine sanft ansteigende Flut (“Rising Tide”) allgemeiner Theorien einhüllt und so aufweicht. Sehr gut: Das ist Deine Arbeitsweise, und was Du getan hast, beweist, dass es tatsächlich funktioniert. Für topologische Vektorräume oder algebraische Geometrie zumindest . . . Es ist nicht so offensichtlich für die Zahlentheorie (bei der die beteiligten Strukturen alles andere als offensichtlich sind - oder vielmehr, bei der alle möglichen Strukturen involviert sind); Ich habe den gleichen Vorbehalt für die Theorie der Modulformen, die sichtbar reicher ist als ihr einfacher „Lie-Gruppen“-Aspekt oder ihr „algebraische Geometrie-Modulschemata"-Aspekt. Deshalb diese Frage: Hast Du in Wirklichkeit nicht zwischen 1968 und 1970 festgestellt, dass die „Rising Tide“-Methode gegen diese Art von Fragen machtlos war und dass ein anderer Stil erforderlich gewesen wäre - den Du nicht mochtest?
Die Veröffentlichung von "Récoltes et Semailles" war Anlaß für eine Sendung von France Culture mit Laurent Lafforgue und zwei weiteren Mathematikern (Olivia Caramello und Alain Connes). Neben Grothendieck und seinem Buch war auch die Topos-Theorie Thema dieser Sendung. In der Topos-Theorie geht es grob gesagt darum, den Begriff des topologischen Raumes durch einen allgemeineren kategorientheoretischen Begriff zu ersetzen. Laurent Lafforgue war seit 2000 einer von sechs Professoren am Institut des Hautes Études Scientifiques, dem wohl wichtigsten französischen Forschungsinstitut für Mathematik und Theoretische Physik. 2002 erhielt er die Fields-Medaille für seinen Beweis der Langlands-Korrespondenz im Funktionenkörper-Fall. In den Jahren danach engagierte er sich für eine Erneuerung ("refondation") des Schulwesens (mehr klassische Sprachen, weniger Naturwissenschaften), war auch kurzzeitig Mitglied im Haut conseil de l'éducation, sowie seit 2013 mit einer Buchveröffentlichung für eine "rationale und rigorose" Analyse des Ukraine-Konflikts. Daneben hat er in den letzten zwanzig Jahren auch noch einige mathematische Arbeiten geschrieben, die aber nicht mehr die Rezeption seiner früheren Arbeiten erhielten. Seine letzte, 2019 erschienene Arbeit mit Olivia Caramello benutzt den Rahmen der Topos-Theorie zur Konstruktion "topologischer Galois-Theorien", d.h. topos-theoretischer Verallgemeinerungen der klassischen Korrespondenz zwischen Körpererweiterungen und abgeschlossenen Untergruppen der Galois-Gruppe. Seit 2019 wurde sein Lehrstuhl von Huawei gesponsort, 2021 verließ er das IHÉS, um ganz bei Huawei Technologies France zu arbeiten. In den letzten zehn Minuten der Sendung bei France Culture ging es um eine "Feindseligkeit" der Mathematiker gegenüber der Topos-Theorie. Caramello meint, dass viele Spezialisten Angst davor hätten, dass Probleme ihrer Spezialitäten mit fremden Methoden gelöst werden könnten. (Sie spricht von Ostrazismus.) Ein Mathematiker hätte nach einem ihrer Vorträge mehrere Stunden nach einem Gegenbeispiel gesucht, weil er ihre Verallgemeinerung eines bekannten Satzes nicht hatte glauben wollen. Auch Lafforgue spricht von einer sehr großen Feindseligkeit gegenüber seinen Arbeiten zur Topos-Theorie. Dagegen habe er zu seiner größten Überraschung bei den Ingenieuren von Huawei sehr viel offenere Ohren gefunden. Dort bei den Verantwortlichen der Forschungsabteilung von Huawei glaube man daran, dass die Topos-Theorie für die Entwicklung einer künstlichen Intelligenz wesentlich werden könnte. Nun ja.
Die Einheit der Mathematik
One may seek unity in mathematics through the eyes of cohomology. Let X be a mathematical object of "dimension" d. The object may be analytic, arithmetic, geometric, or combinatorial, and the precise notion of dimension will depend on the context. Curiously, often it is possible to construct from in a natural way a graded real vector space \(A(X) = \bigoplus_{k=0}^d A_k(X)\). The new object A(X) called the cohomology of X, often encodes essential information on X. When two objects X and Y of the same kind are related in a particular way, the relationship is often reflected on their cohomologies A(X) and A(Y), and this property can be exploited to extend our understanding. Primary consumers of this viewpoint so far were topologists and geometers, and a great number of triumphs in topology and geometry are based on a construction of A(X) from X. Interestingly, sometimes, satisfactory and equally useful cohomologies exist even when X does not have a geometric structure in the conventional sense. In particular, when X is a matroid, the study of A(X) led to proofs of a few combinatorial conjectures that were beyond reach with traditional methods. There are a few pieces of evidence for the unity in the above context. The list is short, but the pattern is remarkable. For example, A(X) can be the ring of algebraic cycles modulo homological equivalence on a smooth projective variety, the combinatorial cohomology of a convex polytope, the Soergel bimodule of a Coxeter group element, the Chow ring of a matroid, the conormal Chow ring of a matroid, or the intersection cohomology of a matroid. (Einleitung zu Huhs ICM-Vortrag.)
Während die Standard-Vermutungen über die Existenz von "Lefschetz-Paketen" auf dem Vektorraum algebraischer Zykel (und damit die Grundlegung für Grothendiecks Theorie der Motive) weiterhin offen sind, hat man (wie im obigen Zitat dargestellt) solche Pakete mit Poincaré-Dualität, schwerem Lefschetz-Satz und Hodge-Riemann-Relationen aber in verschiedenen anderen mathematischen Strukturen gefunden. Die bemerkenswertesten Beispiele sind vielleicht die Arbeiten von Elias und Williamson, die solche Strukturen in der Darstellungstheorie finden, und die erwähnte Arbeit von Adiprasito, Huh und Katz, die solche Strukturen in der Theorie der Matroide findet. Diese Strukturen sind dann wiederum verantwortlich dafür, dass unimodale Polynome in vielen unterschiedlichen Gebieten der Mathematik vorkommen. Grob gesagt folgt aus den Hodge-Riemann-Relationen die Positivität gewisser Determinanten, also Ungleichungen der Form \(a_i^2-a_{i-1}a_{i+1} > 0 \). (Folgen mit dieser Eigenschaft nennt man log-konkav.) Eine Folge von Null verschiedener Zahlen, die diese Ungleichung für alle i erfüllt, ist unimodal. 
In der geometrischen Darstellungstheorie sind die Soergelschen Bimoduln eine zentrale Struktur. Die Soergelschen Bimoduln eines Coxeter-Systems bilden eine monoidale Kategorie, deren Grothendieck-Gruppe mit der Hecke-Algebra übereinstimmt. Elias und Williamson zeigten 2014 die Existenz eines Lefschetz-Pakets auf den Soergelschen Bimoduln und bewiesen damit eine Vermutung Soergels über die Existenz unzerlegbarer Bimoduln, deren Klassen der Kazhdan-Lusztig-Basis in der Hecke-Algebra entsprechen. Daraus folgt die Positivität der Koeffizienten der Kazhdan-Lusztig-Polynome sowie ein algebraischer Beweis der zuvor von Beilinson-Bernstein, Brylinski-Kashiwara und später Soergel mit anderen Methoden bewiesenen Kazhdan-Lusztig-Vermutung, einer Charakterformel für Darstellungen höchsten Gewichts. Man bekommt auch die Unimodalität der Strukturkonstanten der Kazhdan-Lusztig-Basis für die Hecke-Algebra. Wenn das Coxeter-System von einer halbeinfachen Lie-Gruppe kommt, entsprechen die Soergelschen Bimoduln der äquivarianten Schnittkohomologie der zugehörigen Schubert-Varietät und das Lefschetz-Paket entspricht der klassischen Hodge-Theorie. Eine andere Situation, wo man ein Analogon zur Hodge-Theorie hat, ist die kombinatorische Schnittkohomologie von Polytopen, das ist die Schnittkohomologie der zum Polytop zugeordneten torischen Varietät. Die klassischen Dehn-Sommerville-Gleichungen für die Anzahlen d-dimensionaler Seiten des Polytops wurden hier von Stanley mittels Poincaré-Dualität interpretiert. Für diese Schnittkohomologie bewies Peter McMullen 1993 die Existenz von Lefschetz-Paketen und vereinfachte damit Stanleys Beweis der g-Vermutung. (Die g-Vermutung formuliert Bedingungen für den f-Vektor, also den Vektor aus den Anzahlen d-dimensionaler Seiten eines Polytops für d=0,1,... für polytopale Sphären.) In ihrer allgemeinen Form für simpliziale Sphären (und sogar Homologiesphären) wurde die g-Vermutung Ende 2018 von Adiprasito bewiesen, wobei er für den Beweis des schweren Lefschetz-Satzes die Hodge-Riemann-Relationen durch eine noch stärkere Bedingung (Hall-Laman-Relationen) ersetzen mußte. Eine Anwendung war der Beweis der Grünbaum-Kalai-Sarkaria-Vermutung, die für den f-Vektor eines d-dimensionalen Simplizialkomplexes \(\Delta\subset{\bf R}^{2d}\) die Ungleichung \(f_d(\Delta)\le(d+2)f_{d-1}(\Delta)\) behauptete. In der Konvexgeometrie kennt man seit dem Ende des 19. Jahrhunderts die Brunn-Minkowski-Ungleichung für das Volumen von Minkowski-Summen und als weitreichende Verallgemeinerung die Alexandrow-Fenchel-Ungleichungen, deren Beweis von 1938 einen elementaren Fall von Hodge-Riemann-Relationen verwendet. Aus den Alexandrow-Fenchel-Ungleichungen folgt, dass die gemischten Volumina konvexer Körper eine log-konkave (und damit unimodale) Folge bilden. Stanley hatte das in den 1980er Jahren benutzt, um die Log-Konkavität von in der Kombinatorik vorkommenden Folgen zu beweisen. Das kann man als Vorläufer der Arbeit von Huh sehen, die die Log-Konkavität des chromatischen Polynoms von Graphen auf die Alexandrow-Fenchel-Ungleichungen für die gemischten Volumina zugeordneter Gitterpolytope zurückführt. Es war dann die Erkenntnis von Adiprasito, dass man für den Beweis neben den Hodge-Riemann-Relationen auch kombinatorische Versionen des schweren Lefschetz-Satzes und der Poincaré-Dualität formulieren sollte, also ein Analogon des Lefschetz-Pakets, und dass ein kombinatorischer Beweis von McMullens schwerem Lefschetz-Satz alle drei Eigenschaften beweisen und sich auf Matroide übertragen lassen sollte. (Mit einem ähnlichen Ansatz bewies Adiprasito dann auch die g-Vermutung.) Diesen kombinatorisch formulierten schweren Lefschetz-Satz und die Hodge-Riemann-Relationen für Matroide bewiesen Adiprasito, Huh und Katz dann mit rein kombinatorischen Methoden, ohne noch (wie in Huhs Beweis der Unimodalität des chromatischen Polynoms) Bezug auf zu den Matroiden assoziierte Objekte der algebraischen Geometrie zu nehmen. Sie betrachteten Ordnungsfilter von Teilmengen eines Matroids und definierten einen „Flip“, mit dem sie den trivialen Fall des leeren Filters induktiv mit größeren Filtern in Beziehung setzen konnten. Damit konnten sie die Koeffizienten des charakteristischen Polynoms als Produkte von Klassen im Chow-Ring interpretieren und so den schweren Lefschetz-Satz und die Hodge-Riemann-Relationen beweisen - rein kombinatorisch, ohne Rückgriff auf Objekte der algebraischen Geometrie. Es gibt unimodale Polynome noch in vielen weiteren Bereichen der Mathematik, wo es noch keine Erklärung (und keinen Beweis) für die Unimodalität gibt. Zum Beispiel hat Stoimenow vermutet, dass das Alexanderpolynom alternierender Knoten unimodal ist. Vielleicht gibt es also Analoga zu Grothendiecks Standardvermutungen noch sehr viel allgemeiner in aller möglichen Mathematik - irgendeine Metastruktur, die sich dann auf völlig verschiedene mathematische Strukturen anwenden ließe.