Rechenaufgaben zur Tour de France
Aufgaben für die Schule: wie wahrscheinlich ist eine Tour ohne Doping?
Es hat sich ja vielleicht
herumgesprochen, daß es dieses Jahr im NRW-Mathe-Zentralabitur eine Aufgabe über den Basketballer Dirk Nowitzki gab, die leider mit den Angaben der Aufgabenstellung nicht lösbar war. (Gefragt wurde nach der Wahrscheinlichkeit, daß Nowitzki bei höchstens 4 Freiwürfen hintereinander erfolgreich ist. Gegeben war seine Trefferquote von 90,4%, aber nicht die Anzahl der Freiwürfe, die ihm zur Verfügung stehen.)
Aus aktuellem Anlaß folgen hier einige Rechenaufgaben zur Tour de France (die wohl eher für die Primarstufe als für das Abitur geeignet sind).
 1. Streckenlänge
1. Streckenlänge
1988:
3286 Kilometer
2008:
3559 Kilometer
Um wieviel Prozent hat sich die Streckenlänge erhöht?
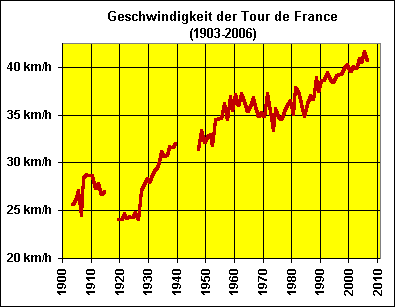
2. Durchschnittsgeschwindigkeit
1988:
38,9 km/h
2008:
41,8 km/h (bisher)
Um wieviel Prozent hat sich die Durchschnittsgeschwindigkeit erhöht?
3. Bergetappen
1988:
6 Bergetappen
2008:
9 Bergetappen
Um wieviel Prozent hat sich die Zahl der Bergetappen erhöht?
4. Wahrscheinlichkeit
Wie wahrscheinlich ist es, daß solche Leistungssteigerungen
ohne Doping möglich sind?
PS: Ich habe diesen Artikel schon vor einer Woche geschrieben, wollte mit dem In-das-Netz-Stellen aber bis zum
ersten bewiesenen Doping-Fall warten. Man soll ja niemanden vorverurteilen.
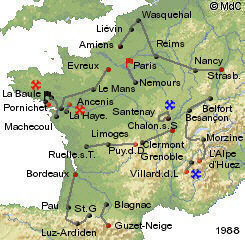 (https://www.memoire-du-cyclisme.net/eta_tdf_1984_1993/tdf1988.php)
(https://www.memoire-du-cyclisme.net/eta_tdf_1984_1993/tdf1988.php)
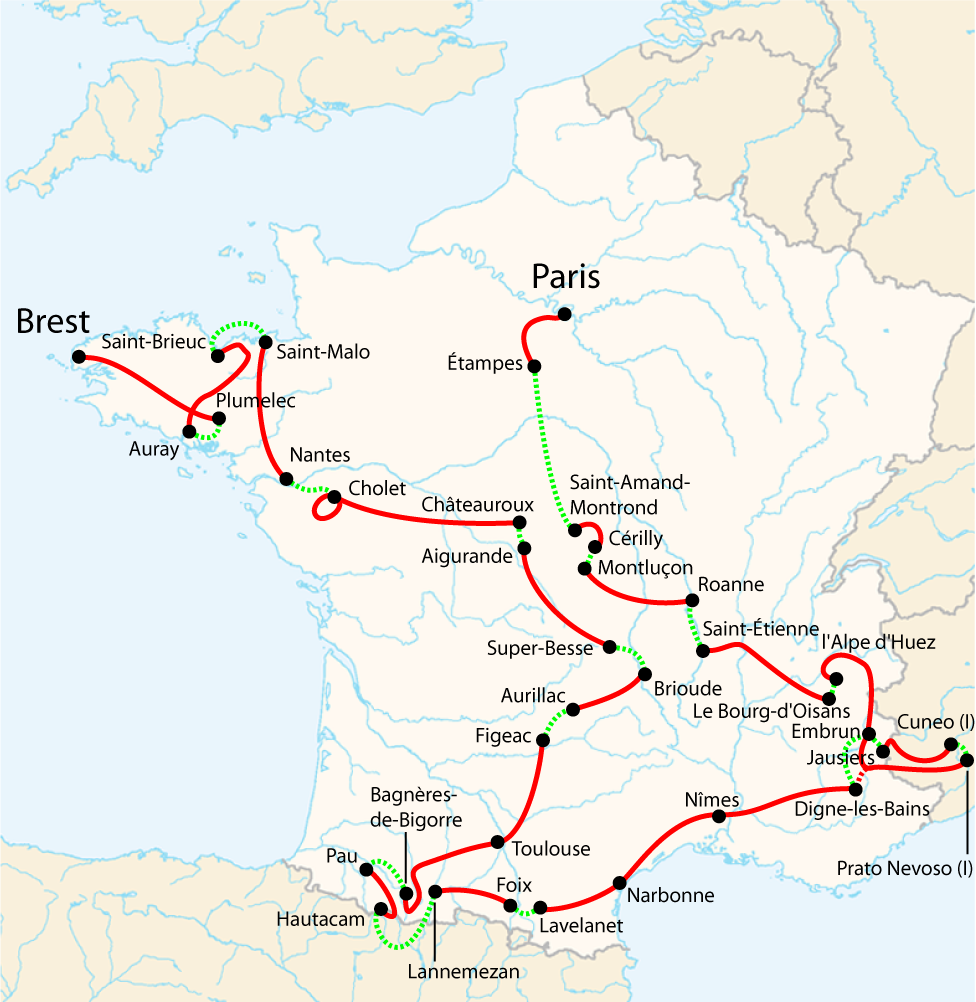
2008
(Wikipedia)
 1. Streckenlänge
1988: 3286 Kilometer
2008: 3559 Kilometer
Um wieviel Prozent hat sich die Streckenlänge erhöht?
2. Durchschnittsgeschwindigkeit
1988: 38,9 km/h
2008: 41,8 km/h (bisher)
Um wieviel Prozent hat sich die Durchschnittsgeschwindigkeit erhöht?
3. Bergetappen
1988: 6 Bergetappen
2008: 9 Bergetappen
Um wieviel Prozent hat sich die Zahl der Bergetappen erhöht?
4. Wahrscheinlichkeit
Wie wahrscheinlich ist es, daß solche Leistungssteigerungen ohne Doping möglich sind?
PS: Ich habe diesen Artikel schon vor einer Woche geschrieben, wollte mit dem In-das-Netz-Stellen aber bis zum ersten bewiesenen Doping-Fall warten. Man soll ja niemanden vorverurteilen.
1. Streckenlänge
1988: 3286 Kilometer
2008: 3559 Kilometer
Um wieviel Prozent hat sich die Streckenlänge erhöht?
2. Durchschnittsgeschwindigkeit
1988: 38,9 km/h
2008: 41,8 km/h (bisher)
Um wieviel Prozent hat sich die Durchschnittsgeschwindigkeit erhöht?
3. Bergetappen
1988: 6 Bergetappen
2008: 9 Bergetappen
Um wieviel Prozent hat sich die Zahl der Bergetappen erhöht?
4. Wahrscheinlichkeit
Wie wahrscheinlich ist es, daß solche Leistungssteigerungen ohne Doping möglich sind?
PS: Ich habe diesen Artikel schon vor einer Woche geschrieben, wollte mit dem In-das-Netz-Stellen aber bis zum ersten bewiesenen Doping-Fall warten. Man soll ja niemanden vorverurteilen.
 (https://www.memoire-du-cyclisme.net/eta_tdf_1984_1993/tdf1988.php)
(https://www.memoire-du-cyclisme.net/eta_tdf_1984_1993/tdf1988.php)
 2008 (Wikipedia)
2008 (Wikipedia) 


