Leibniz oder Madhava?
Bekanntlich gibt die Taylor-Reihe des Arkustangens mit \( x=1\) die Formel \[ \frac{\pi}{4}=\sum_{k=0}^{\infty} \frac{(-1)^k}{2k+1} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \dotsb.\]
Die wird in europäischen Kulturen meist als Leibniz-Reihe bezeichnet, war aber dem indischen Mathemtiker Madhava bereits im 14. Jahrhundert bekannt, veröffentlicht etwa hundert Jahre später um 1500 in der von Nilakantha Somayaji in 432 Sanskrit-Versen in acht Kapiteln geschriebenen astronomischen Abhandlung Tantrasamgraha
Für praktische Berechnungen ist die Reihe wenig geeignet, wie man sich leicht durch Berechnen einiger Partialsummen plausibel machen kann. Tatsächlich braucht man \( \frac{1}{2}10^s \) Summanden für die Berechnung der ersten \(s\) Nachkomastellen.
Strings
Im Juni ging durch die Medien, dass man als Anwendung der Stringtheorie jetzt die Kreiszahl \( \pi \) besser berechnen könne. Zunächst von indischen Medien gehypt („Indian physicists untangle new pi series that could change maths forever“ hieß die Überschrift auf India Today), fand es die Pressemitteilung über eine am 28. Mai von zwei Physikern in Physical Review Letters veröffentlichte Arbeit „Field Theory Expansions of String Theory Amplitudes“ dann auch in große europäische Zeitungen. Tatsächlich hatten zwei indische Stringtheoretiker eine neue Formel für die Kreiszahl \( \pi \) gefunden:
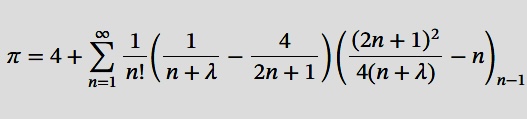
Dabei ist \( \lambda \) eine beliebige komplexe Zahl und der Index \( n-1 \) steht für das Pochhammer-Symbol
\( \left(x\right)_n=x(x+1)\ldots(x+n-1)\).
Die Reihe konvergiert immerhin schneller als die Madhava-Reihe, freilich nicht schneller als andere bekannte Entwicklungen wie etwa die der Chudnovskys.
In stringkritischen Blogs wurde die Berichterstattung dann auch eher als weiteres Beispiel schlechten Wissenschaftsjournalismus wahrgenommen. Not even wrong berichtete unter der ironischen Überschrift „Latest Breakthrough from String Theory“. Ein besorgter indischer Mathematiker kommentierte dort: "India at the moment is hyper-nationalistic, so such exaggerated news coverages aren’t uncommon (in fact they are extremely common).“
Auf https://mathoverflow.net/questions/473931/possible-new-series-for-pi wurde schließlich die Frage diskutiert, was aus Mathematiker-Sicht von der Formel zu halten ist und ob sie überhaupt neu sei. Repräsentativ die Antwort von Jesus Guillera:
I have not seen this formula for \( \pi \) before in the literature despite that I know many other formulas. Although the series is not good for computing \( \pi \) (contrary to what is stated in the press), it could have some interest. In the paper there is also a formula of the same style for \( \zeta(2) \). Taking the limit of it as \( \lambda\to\infty \) we obtained a well-known alternating series with a better convergence.
Wie viele Stellen von Pi braucht man?
Wikipedia liefert da ein paar prägnante Beispiele: Um den Umfang eines Kreises bis auf 1 mm genau zu berechnen braucht man: bei einem Radius von 30 Metern vier Dezimalstellen, beim Erdradius zehn Dezimalstellen, bei einem Radius mit dem Abstand Erde-Sonne 15 Dezimalstellen. Und um den größten in unserem Universum vorstellbaren realen Kreis mit der Genauigkeit einer Planck-Länge zu berechnen reichen 62 Dezimalstellen.
Aber natürlich kommt \( \pi \) in der Mathematik und Physik überall vor, nicht nur bei der Berechnung von Kreisumfängen: Bei der Berechnung der Riemannschen Zeta-Funktion, in Fourier-Transformationen, wie sie etwa bei der Heisenbergschen Unschärferelation vorkommen, in den Feldgleichung der Allgemeinen Relativitätstheorie.
Wieviele Stellen von \( \pi \) braucht man also in physikalischen Anwendungen? Es gibt ein Committee on Data for Science and Technology , das die zu verwendenden Werte vieler Naturkonstanten festlegt. \( \pi \) selbst wird von ihnen nicht berechnet, aber natürlich alle möglichen von \( \pi \) abhängenden Naturkonstanten. Die Mitarbeiter benutzen für ihre Berechnungen immerhin 32 Stellen von \( \pi \). Das sind doppelt so viele bei der NASA, die ihre Raumschiffe mit nur 16 \( \pi \)-Stellen steuert.
Was man wirklich nicht braucht
Vor ungefähr zehn oder zwölf Jahren gab es mal eine (immerhin kostenlose) App, mit der man „beliebig viele“ (tatsächlich maximal hunderttausend) Stellen der Kreiszahl \( \pi \) berechnen konnte. Ein 1,8MB großes Programm, das einen 100KB großen konstanten String ausgeben konnte. Tausend oder zweitausend Stellen wurden praktisch instantan berechnet, bei zwanzigtausend Stellen dauerte es schon einige Sekunden und für hunderttausend Stellen brauchte man etwas Geduld.
Die App gibt es nicht mehr, dafür kann man im AppStore heute (zunächst kostenlos, für speziellere Funktionen dann aber 3,99) eine App erwerben, mit der sich die Ziffern von \( \pi \) üben lassen. „Pi mit einem Quiz auswendig“ verspricht die Werbung. Das Spiel besteht dann aber einfach nur daraus, dass man die Ziffern von \( \pi \) eingibt und verloren hat, sobald man eine Ziffer falsch eingibt. Das kann man dann beliebig oft wiederholen.
Beweise ohne Worte
Wie sieht man auf Anhieb, dass \( \pi\) größer als 3, oder äquivalent dass der Umfang des Einheitskreises größer als 6 ist?
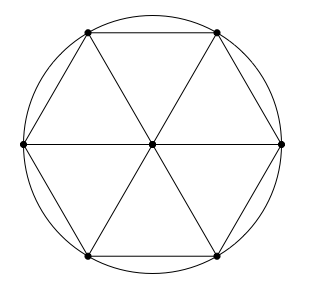
Quelle: https://mathoverflow.net/questions/8846/proofs-without-words
Noch einfacher sieht man, dass \( \pi\) kleiner als 4 ist: Man umschreibt den Einheitskreis durch ein Quadrat der Kantenlänge 2 und vergleicht die Flächeninhalte.
Tau statt Pi
Der Beweis ohne Worte zeigt ja eigentlich eine Abschätzung für \( \tau=2\pi \). Das erinnert mich daran, dass seit vierzehn Jahren von dem Lernsoftware-Unternehmer Michael Hartl propagiert wird, statt des Pi-Tag am 14. März den Tau-Tag am 28. Juni zu feiern. Dafür organisiert er jährliche Events, unterstützt z.B. von Elon Musk und Vitalik Buterin, die von diesem Jahr kann man auf https://www.michaelhartl.com/state-of-the-tau-2024 ansehen.
Hartls Meinung nach sollte die Mathematik des Kreises in der Schule nur noch mit \( \tau\) gelehrt werden. Statt \( U=2\pi r \) hieße es dann \( U=\tau r \), statt \( A=\pi r^2 \) hätte man \( A=\tau\frac{r^2}{2} \), und Sinus und Kosinus wären \( \tau-\) statt \( 2\pi- \)periodisch.
Ich halte die Wahl der Konstanten ja eher für irrelevant. Schließlich soll man Formeln verstehen statt sie auswendig zu lernen – und für die Verstehbarkeit spielt der Faktor 2 sicher keine Rolle. Wie man dem Artikel https://www.spiegel.de/wissenschaft/mensch/revolution-gegen-die-kreiszahl-physiker-will-pi-abschaffen-a-771007.html auf Spiegel Online entnehmen kann, halten auch deutsche und österreichische Didaktiker diese Neuerung für überflüssig, sehr beruhigend.
Auf Hartls Website findet sich auch der überschwängliche Dankesbrief eines anonymen Studenten, der seiner kleinen, Matheunterricht-geplagten Schwester mittels Tau angeblich zum unverhofften Erfolg in einer Trigonometrie-Klausur verhalf. Derartige Fälle kann sich freilich Rudolf vom Hofe von der Gesellschaft für Didaktik der Mathematik nicht so recht vorstellen (zitiert aus Spiegel Online):
"Ich glaube nicht, dass durch diese Verdopplung die entsprechenden Formeln plötzlich allen einleuchten", sagt der Bielefelder Professor. Und überhaupt habe die Mathematik in der Schule genug echte Probleme. Auch seine Klagenfurter Kollegin Edith Schneider sieht keine wirkliche Vereinfachung: An Pi führe derzeit schließlich kein Weg vorbei. "Tau wäre doch nur wieder ein neues, zusätzliches Symbol, das ich mir als Schüler dann auch noch merken soll."
Annäherungen
Neben dem Pi-Tag am 14. März und dem Tau-Tag am 28. Juni gibt es auch noch den Pi-Approximations-Tag am 22. Juli. Die Annäherung \( \frac{22}{7}\approx\pi \) ist das Thema des folgenden Bildes von
https://singingbanana.tumblr.com/post/7921183215/reposting-this-for-pi-approximation-day

Für nicht-frankophone Leser: ‘ceci n’est pas une pi’ bedeutet ‘das ist kein Pi’, das Bild und der Text sind eine Variation auf ‘ceci n’est pas une pipe’ (‘das ist keine Pfeife’) von Magritte. Dieses bekannte Gemälde (das ich hier aus Urheberrechtsgründen nicht zeigen kann) wird meist interpretiert als Demonstration, daß selbst die realistischste Abbildung eines Objekts nicht das Objekt selbst ist.



