Der Standard schrieb vor einigen Monaten in einem Artikel Neue mathematische Kachelformen zum Auslegen von Flächen entdeckt , dass erstmals Formen mit abgerundeten Ecken zur Parkettierung beschrieben wurden, die in der Natur weit verbreitet sind und überraschende Eigenschaften haben.
Es geht um die Arbeit Soft cells and the geometry of seashells von Domokos, Goriely, Horváth und Regös, erschienen am 10. September in PNAS Nexus.
Das Signifikanzstatement sagt (meine Übersetzung):
Polygonale und polyedrische Parkettierungen, bestehend aus Zellen mit flachen Seitenflächen und spitzen Ecken, sind erfolgreiche Modelle in Geologie, Physik und Chemie, die Phänomene von Rissnetzwerken bis hin zu Konvektionszellen, Schäumen und supramolekularen Mustern beschreiben. Diese Modelle beschreiben jedoch nicht die Vielfalt stark gekrümmter geometrischer Formen in der Biologie. Hier führen wir eine neue Klasse von Parkettierungen ein, sogenannte weiche Parkettierungen, deren Zellen stark gekrümmte Seitenflächen haben, und die möglichst wenige spitze Ecken minimal haben, was Einschränkungen des biologischen Wachstums imitiert. Wir beweisen einen Satz, der zeigt, dass weiche Parkettierungen im kombinatorischen Sinne häufig sind, und wir zeigen, dass diese geometrischen Formen in natürlichen Beispielen, von biologischen Zellen bis hin zu den Kammern von Meeresmuscheln, einschließlich des Nautilus, überzeugend vorkommen.
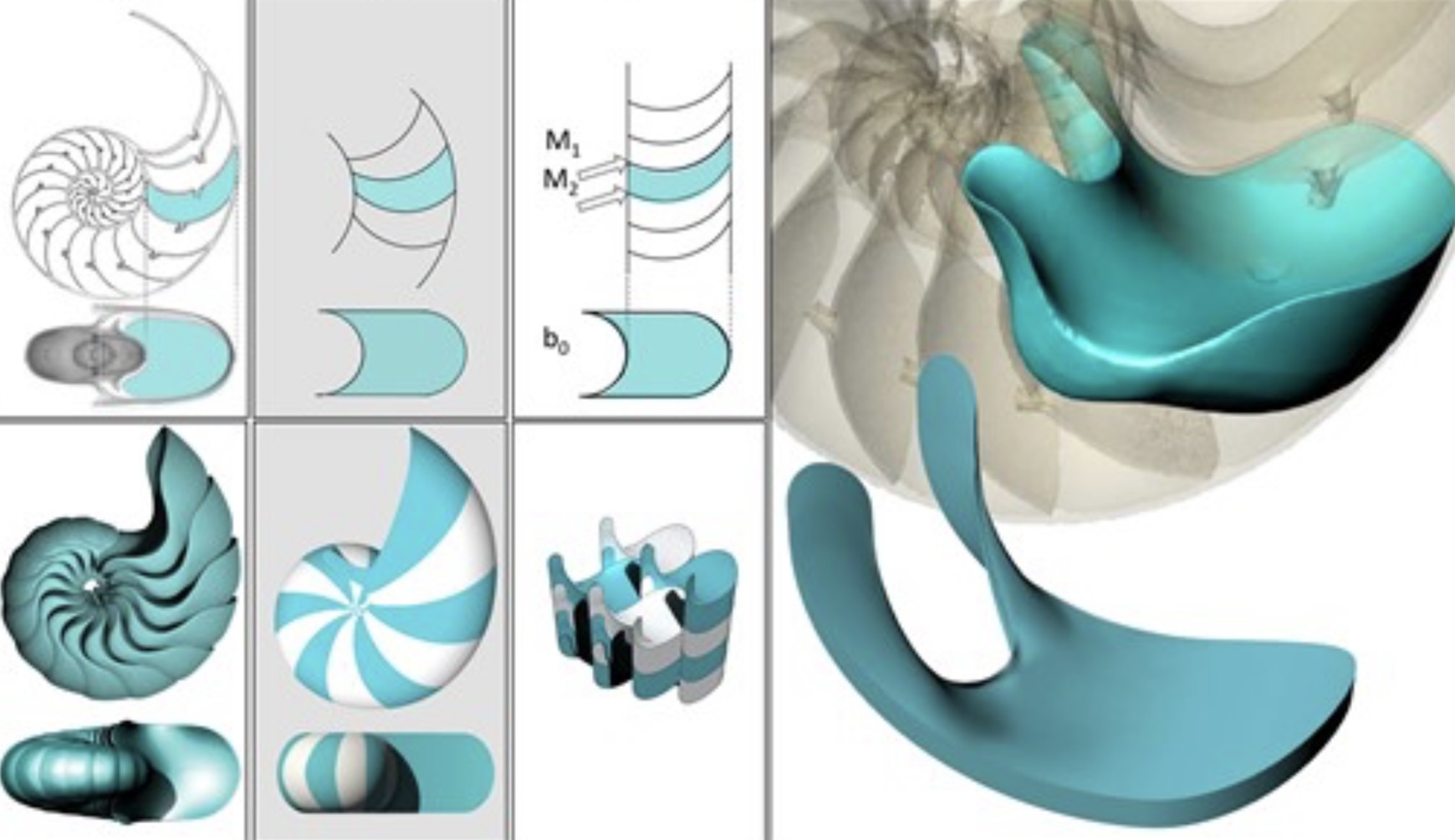
Dieses Bild aus der Arbeit zeigt, wie polygonale Parkettierungen zu weichen Parkettierungen gemacht werden können.
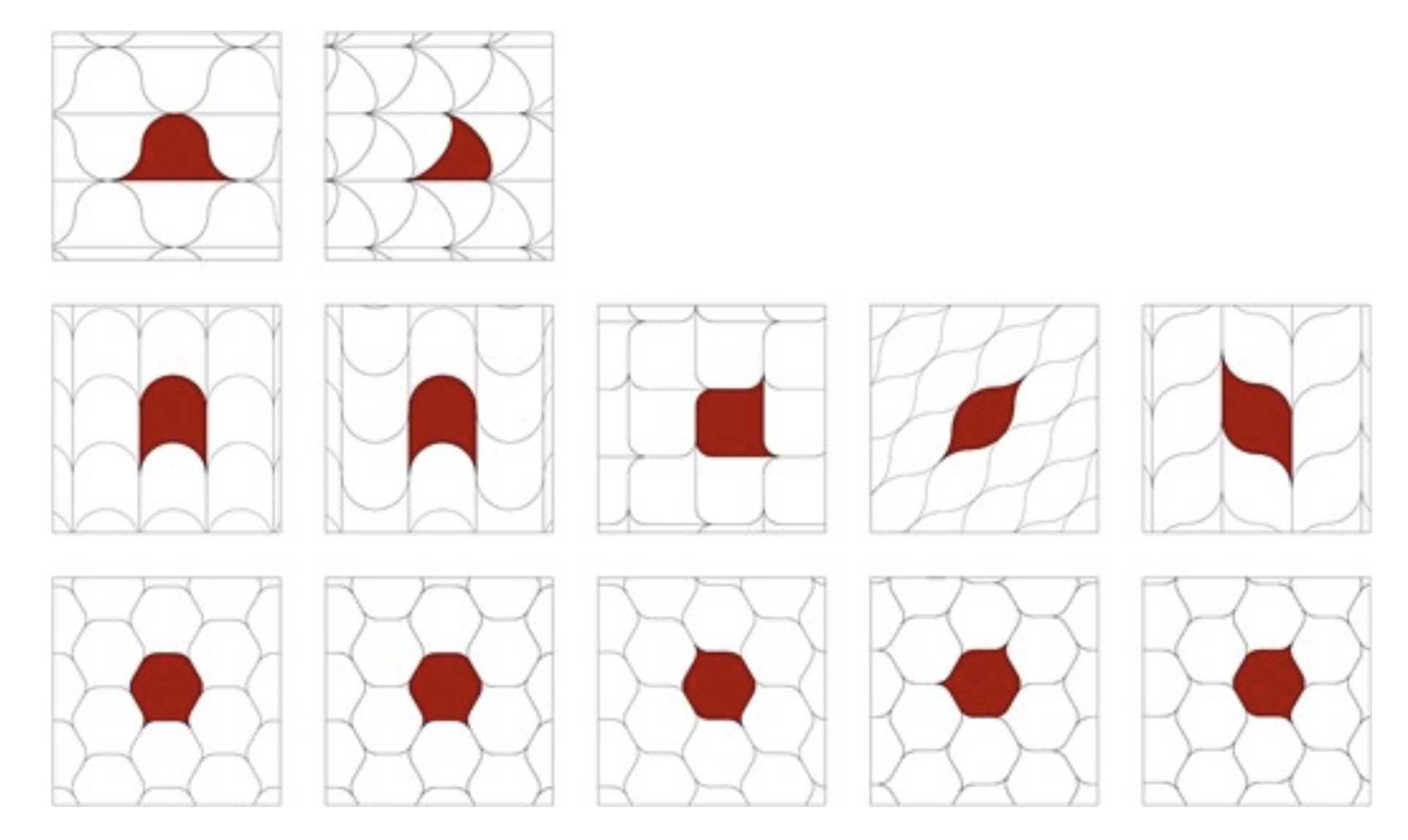
Weder die Ebene noch der Raum können auf stetig differenzierbare Weise parkettiert werden: die Autoren zeigen, dass die Teile einer Parkettierung der Ebene bzw. des Raumes mit dreieckigen bzw. tetrahedralen Teilen immer mindestens drei bzw. mindestens vier spitze Ecken haben müssen. Allgemeiner müssen bei einer Parkettierung der Ebene die Teile immer mindestens zwei spitze Ecken haben. Überraschend zeigen die Autoren aber, dass man für Parkettierungen des Raumes die spitzen Ecken häufig vermeiden kann.
Der Hauptsatz der Arbeit besagt:
Let M be a balanced, normal convex tiling and let V(M) denote the set of the duals of vertex polyhedra in M. If every polyhedron P in V(M) has a Hamiltonian circuit, then there exists a soft polyhedric tiling M‘ which is combinatorially equivalent to M.
Die Autoren glauben, dass man diese Bedingungen noch abschwächen kann und dass vermutlich sogar gilt:
Let M be a balanced, normal, convex tiling. Then, there exists a combinatorially equivalent, soft polyhedric tiling M‘.
Der Artikel in Der Standard erklärt, dass die rundesten Lösungen dazu tendieren, flügelartige Ausformungen zu entwickeln, und dass diese Formen sich auch in der Natur finden: